DES算法流程

初始置换IP

表格的使用方法: 将输入的64bit的明文从1开始标号，依次放入到IP初始置换表中数字对应的位置。填充完毕后，按照行优先的顺序从第1行开始依次读取获得输出。

16轮轮结构

整体结构

因为这16轮的操作都是一样的，所以这里我们只介绍第一轮的操作

1. 将上一步经过初始置换IP后的64bit的结果平分为两部分(每部分32bit)，分别记为$L_0$ 和 $R_0$

2. 对$R_0$进行一次F函数的变换并与$L_0$进行异或，结果作为$R_1$，$R_0$作为$L_1$

   即:

   $L_i = R_{i-1}$

   $R_i = L_{i-1} \oplus F(R_{i-1}, K_i)$

3. 进行下一轮

F函数

F函数是对$R_i$进行操作这一前提条件之后不再重复

1. E盒扩展

   

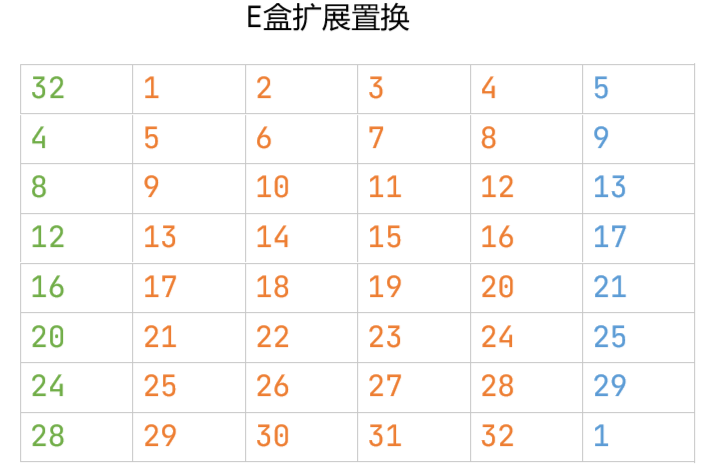
   同初始置换IP的步骤相同，按照顺序将输入的$32bit$依次放入对应的位置，仍按照行优先输出，输出结果为$48bit$

2. E盒扩展结果与48bit的轮子密钥进行异或

3. S盒代替压缩

   将$48bit$分为$8$组，每组$6bit$，依次编号为$B_1,B_2,...B_8$

   一共有$8$个S盒，依次编号为$S_1,S_2,...S_8$

   $B_i$对应着使用$S_i$

   考虑$B_1$，$B_1 = b_1b_2b_3b_4b_5b_6$,我们定义$r = 2*b_1+b_6, c = 2^3b_2+2^2b_3+2b_4 + b5$(即将二进制转化为十进制)，我们去$S_1$盒中找到$r$行$c$列对应的十进制数，将其转化为4位二进制即为结果

   参照$B_1$的方法，依次转化完余下$5$组，最终得到$32bit$的输出

4. p盒置换

   使用下表进行p盒置换，使用方法和IP初始置换相同

   

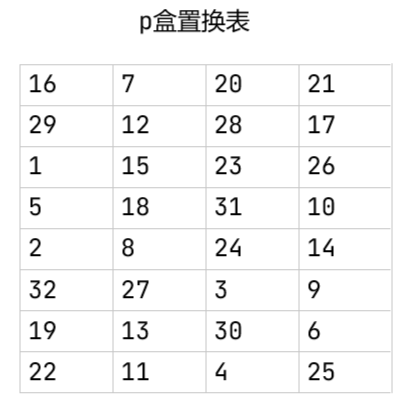
逆初始置换

16轮轮结构最后得到64位的输出，使用逆初始置换表将数据进行重新编排，使用方法同IP初始置换

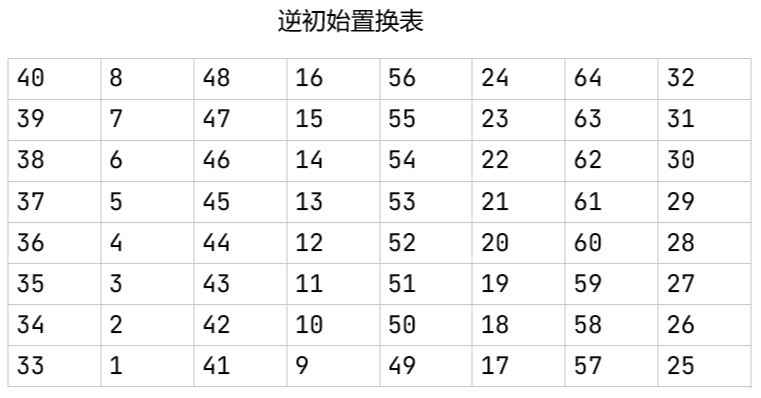
子密钥生成

1. 置换选择

置换选择PC-1输入64bit的原始密钥，输出56bit

若输入为56bit，则需要在$8, 16, 24, 32, 40, 48, 56, 64$ bit处分别插入$0,0,1,0,0,0,1,0$ 变为64bit

使用下表格进行置换选择PC-1，仍然是按照先后顺序将原始序列中的每一位填入下表，表格中缺少8的倍数，从而将输入的64bit变为输出的56bit，读取时仍为行优先。

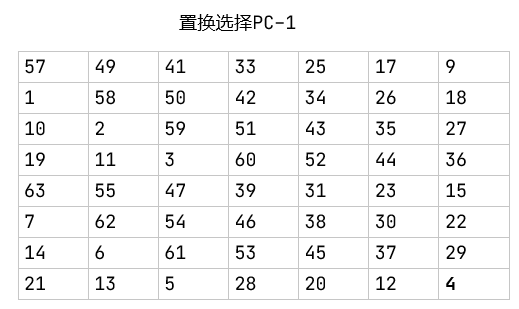
2. 循环移位

   将置换选择PC-1之后得到56bit的输出平分为两部分，各为28bit，即为$C_0$, $C_1$

   根据下标判断需要移动多少位

   

   所谓循环移位是指将$C_0$, $C_1$均看为一个循环的序列，左移1位将最左侧的一位移动到序列的尾部

   eg: 1 0 0 1 -> 0 0 1 1