树形dp

没有上司的舞会

问题描述

Ural大学有\(N\)名职员，编号为\(1~N\)。
他们的关系就像一棵以校长为根的树，父节点就是子节点的直接上司。
每个职员有一个快乐指数，用整数 \(H_i\) 给出，其中 \(1≤i≤N\)。
现在要召开一场周年庆宴会，不过，没有职员愿意和直接上司一起参会。
在满足这个条件的前提下，主办方希望邀请一部分职员参会，使得所有参会职员的快乐指数总和最大，求这个最大值。

问题分析

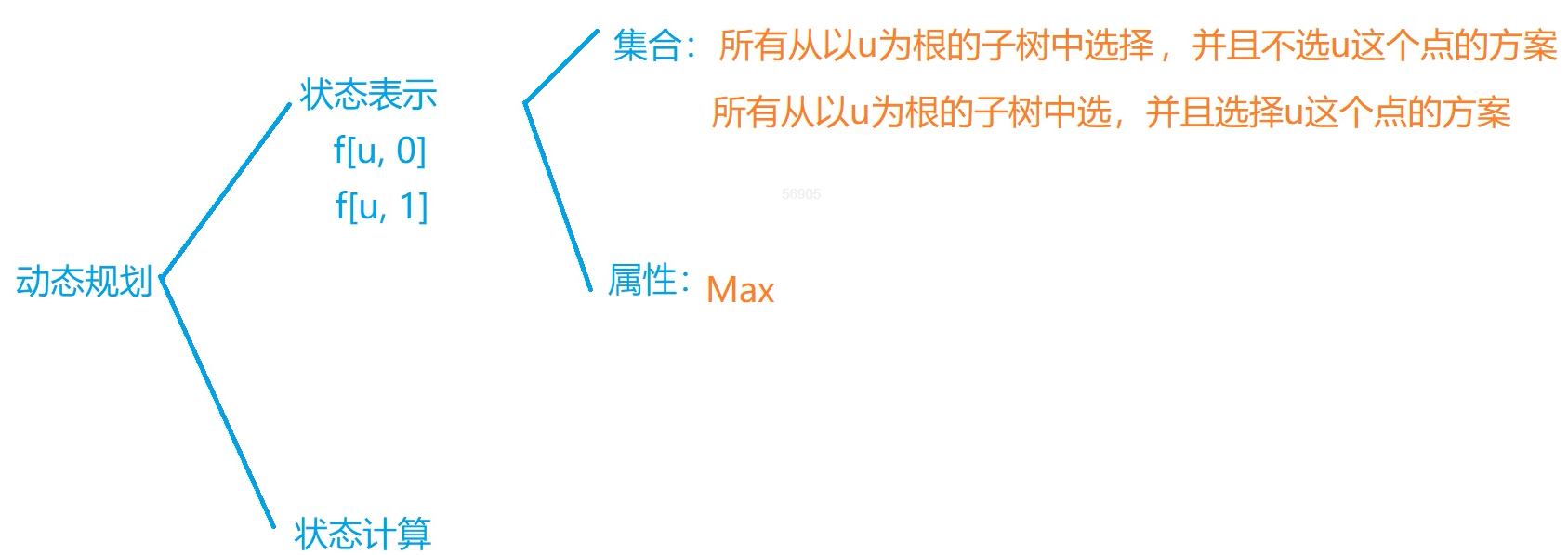
其实状态表示已经为状态计算做好了铺垫，我们只需要分别计算两种状态即可，当选择根节点u时，儿子节点j不能再选择则将f[j][0]累加到f[u][1]，不选择u时选择f[j][0]和f[j][1]中的较大者累加到f[u][0]
本题分析时用到的dp的思想，但是代码实现需要使用递归，所以实现起来更像是搜索。

代码实现

#include <iostream>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 6010;

int n;
int h[N];
int f[N][2];
int head[N], e[N], ne[N], idx;
bool is_father[N]; // 用于判断某点是否为根节点，因为算法需要从根节点开始

void add(int a, int b)
{
    e[idx] = b;
    ne[idx] = head[a];
    head[a] = idx ++;
}
void dfs(int u)
{
    f[u][1] = h[u];
    
    for (int i = head[u]; i != -1; i = ne[i]) // 遍历u的所有儿子节点
    {
        int j = e[i];
        dfs(j); // 在更新u节点的值时需要首先递归求解其儿子节点j的值
        
        f[u][1] += f[j][0]; // u的儿子节点不能选择不代表这一棵子树就没有值
        f[u][0] += max(f[j][0], f[j][1]);
    }
}
int main()
{
    cin >> n; 
    for (int i = 1; i <= n; ++ i) cin >> h[i];
    
    memset(is_father, true, sizeof is_father);
    memset(head, -1, sizeof head);
    for (int i = 0; i < n - 1; ++ i) 
    {
        int a, b;
        cin >> a >> b;
        add(b, a); // 根据树形dp集合的表示，我们需要能够从根节点找到它的儿子节点，所以是b指向a
        is_father[a] = false;
    }

    // 找到根节点
    int root;
    for (int i = 1; i <= n; ++ i) 
        if (is_father[i])
        {
            root = i;
            break;
        }
    
    dfs(root);
    
    cout << max(f[root][0], f[root][1]) << endl;
    
    return 0;
}