中国剩余定理及其扩展

\[\left \{ \begin{aligned} x_1 = a_1 \ (mod \ m_1) \\ x_2 = a_2 \ (mod \ m_2) \\ . \qquad \qquad \\ . \qquad \qquad \\ . \qquad \qquad\\ x_n = a_k \ (mod \ m_k) \end{aligned} \right . \]

中国剩余定理

算法流程

计算所有模数的积 M；
对于第 i 个方程：
a. 计算 \(n_i \ = \ \frac{M}{m_i}\)；
b. 计算 \(n_i\) 在模 \(m_i\) 意义下的逆元 \(n_i^{-1}\)；
方程组的唯一解为: \(x = \sum_{i = 1}^k (n_i * n_i^{-1} * a_i) \ (mod \ M)\)。

代码实现

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long LL;

const int N = 15;
int A[N], B[N];

LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1;
        y = 0;
        return a;
    }
    LL gcd = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return gcd;
}
int main()
{
    int n;
    cin >> n;
    
    // 第一步: 计算所有模数的积M
    LL M = 1;
    for (int i = 0; i < n; ++ i)
    {
        cin >> B[i] >> A[i];
        M *= B[i];
    }

    LL res = 0;

    for (int i = 0; i < n; ++ i)
    {
        
        // LL ni = M / B[i]; 
        // LL ti = qpow(ni, B[i] - 2, B[i]); // B[i] - 2为负数qpow无法处理 题目中只说到任意两个B[i]互质，但没说一定是质数，所以不满足费马小定理的条件
        LL ni = M / B[i], ti, x; // 第二步a: 计算ni
        exgcd(ni, B[i], ti, x); // 第二步b: 计算ni的逆元ti
        
        res = (res + ni * ti % M * A[i] % M) % M; //第三步: 计算答案
    }

    cout << (res % M + M) % M << endl; // 保证M是大于0的最小值
    
    return 0;
}

扩展中国剩余定理

当满足中国剩余定理条件时也可以使用下面的计算方法计算，因为下面的方法没有什么限定条件
中国剩余定理要求 \(m_1, \ m_2, \ ... \ m_n\) 必须是两两互质的，如果不满足这个条件时，就需要使用其它方法来做了
我记得书上有种做法，但是记不清怎么搞的了，待定。

推导过程

问题和对应的推导过程

网上找的推导过程

手写推导过程

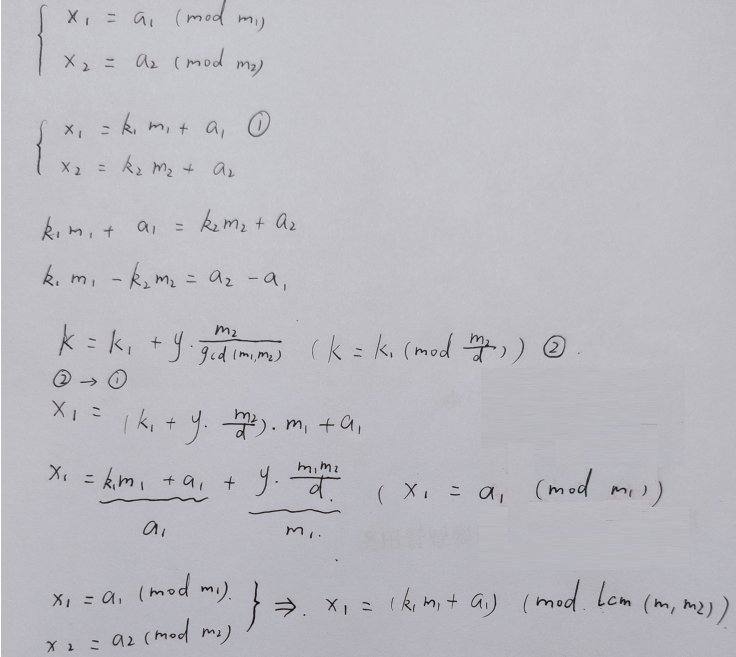
简单地说就是对于多个式子，我们每次只看两个式子，通过数学推导将其等价变形为一个式子，逐渐将所有式子合并最终得到x的解

需要注意的问题

图1的4式是减法，但是扩展欧几里得计算的是加法( \(k_1 \ a_1 + k_2 \ a_2 = m_2 - m_1\) )，出现的问题只不过是其实我们实际计算的其实是k2'，而k2' = -k2，但是这并不会对我们的后续操作产生什么影响，因为我们用的是k1，后面并没有用到k2，而无论是加法还是减法，k1求解出来的值都是一样的。

代码实现

/**
 * 给定 2n 个整数
 * a1,a2,…,an 和 m1,m2,…,mn,
 * 求一个最小的非负整数 x，满足∀i∈[1,n],x≡ai(mod mi)
 * 其实代码只需要按照我们的推导过程直译即可
 */

#include <iostream>

using namespace std;

typedef long long LL;
LL exgcd(LL a, LL b, LL &x, LL &y)
{
    if (!b)
    {
        x = 1, y = 0;
        return a;
    }
    LL d = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return d;
}

int main()
{
    int n;
    cin >> n;
    
    LL m1, a1; // 因为一次合并后m1存储的就是m1和m2的最小公倍数了，是有可能会爆int的
    cin >> m1 >> a1;
    
    LL res;
    for (int i = 0; i < n - 1; ++ i)
    {
        LL m2, a2;
        cin >> m2 >> a2;
        
        LL k1, k2;
        LL d = exgcd(m1, m2, k1, k2);
        
        if ((a2 - a1) % d)
        {
            res = -1;
            break;
        }
        
        k1 *= (a2 - a1) / d; // 正解中对k1还有其它处理
        /**
         * 作用是保证k1为最小非负值
         * 可是为什么需要保持k1为非负值？
         * 这里我忽略了取余的另一个作用就是缩小数据
         * 首先我们必须明确的一点是根据推导过程可知，所有的 k = k1 (mod (m2 / d))，这样的k都是k1的一个解，只需要k2对应变化即可
         * 在下面的步骤中，我们计算res和a1都需要用到k1，本题数据比较极限，如果k1过大，会导致下面的计算结果溢出，所以这里需要取k1的最小非负整数解
         */
        k1 = (k1 % (m2/d) + m2/d) % (m2/d);
        
        res = k1 * m1 + a1;
        
        a1 = m1 * k1 + a1;
        m1 = m1 / d * m2;
    }
    
    /**
     * 最终合并结果就剩下了一个式子 x = a1 (mod m1)
     * 题目要求求解最小的非负整数解
     * 所以可以按照下面的方法做,需要注意res为-1的无解情况
     * 那么为什么正解不可能是-1？？？？？？？？？？？？？？？
     */
     /**
      * 需要特判-1的样例
      * 5
      * 35 30
      * 22 2
      * 16 5
      * 28 23
      * 32 18
      * 
      * 实际输出：769
      * 正确输出：-1
      */
    if (res != -1) res = (res % m1 + m1) % m1;
    
    cout << res << endl;
}

posted @ 2021-02-04 17:14 0x7F 阅读(178) 评论(0) 编辑收藏举报

刷新页面返回顶部

ghy

中国剩余定理及其扩展