模拟哈希表
说明
需要注意的是，这里的模板和数据结构课程中所说的有些区别，主要体现在以下几点:
- 此模板主要是为了解决算法题，所以会采用尽可能简单的实现形式
- 开放地址法采用的是线性探测法，但是数据结构中的线性探测是下面图片这样的,而这里的线性探测用的表长和哈希函数的mod值是一样的
一般哈希
链地址法
/**
* 哈希冲突解决方法1：拉链法(数据结构中叫做链地址法)，就是把哈希值相同的元素放到同一个链表中，即一个哈希值对应一个链表
* 所以这种方法的实质就是数组模拟单链表的应用, 区别在于由一个单链表变成了多个单链表
*/
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003;
int n;
int head[N], e[N], ne[N], idx; // 每一个head都表示着每一个链表的第一个节点编号,初始值为-1代表节点为空
void insert(int x)
{
int k = (x % N + N) % N; // + 是为了解决负数的问题
e[idx] = x;
ne[idx] = head[k];
head[k] = idx ++;
}
bool find(int x)
{
int k = (x % N + N) % N;
for (int i = head[k]; i != -1; i = ne[i])
if (e[i] == x)
return true;
return false;
}
int main()
{
cin >> n;
memset(head, -1, sizeof head);
while (n --)
{
int x;
string op;
cin >> op >> x;
if (op == "Q")
{
if (find(x)) cout << "Yes" << endl;
else cout << "No" << endl;
}
else insert(x);
}
return 0;
}
开放寻址法
/**
* 哈希冲突解决方法2：开放寻址法(下面代码用的是线性探测，但是此处是简化了的，有很多细节并没有体现出来)
* 就是多开一些空间(一般是原数据范围的2到3倍)，然后每次发生冲突时看后面有没有空间
* 查找的时候从映射值之后开始找，要么找到那个值，那么找到空值
* 找到那个值说明找到了，如果找到空值说明哈希表中没有这个元素，因为如果有这个元素，既然这个位置是空，那一定是可以放置在这里的，既然没放说明没有这个元素
*/
#include <iostream>
#include <cstring>
using namespace std;
const int N = 200003, null = 0x7f7f7f7f; // 理论上这里的空值只需要选择一个在-1e9~1e9之外的数即可，但是考虑到数组初始化时需要全部赋值为空，为了操作的简便，这里采用一个大于1e9的十六进制数
int n;
int head[N]; // 实际数据范围是1e5，这里的N已经是扩大2倍后的了
inline int find(int x) // 当x存在时返回它的位置，当它不存在时返回应该存放的位置
{
int k = (x % N + N) % N;
while (head[k] != null && head[k] != x) // 在没有找到要找的数据并且非空位置时就往后找
{
++ k;
if (k == N) k = 0;
}
// 退出循环有两种情况，要么找到空位置了，要么找到它所在的位置，返回k和上面我们说到的这个函数的功能是吻合的
return k;
}
inline void insert(int x)
{
head[find(x)] = x;
}
int main()
{
cin >> n;
memset(head, 0x7f, sizeof head);
while (n --)
{
int x;
string op;
cin >> op >> x;
if (op == "Q")
{
if (head[find(x)] != null) cout << "Yes" << endl; // 注意find返回的是位置，是否等于null看的是这个位置的数
else cout << "No" << endl;
}
else insert(x);
}
return 0;
}
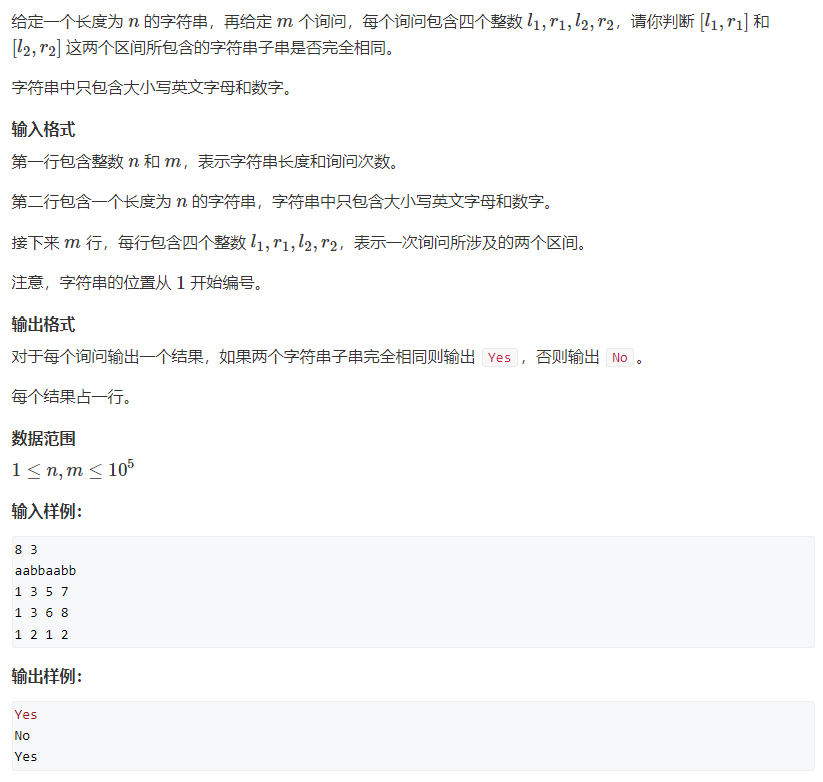
字符串哈希
说明
核心方法就是将字符串看为一个P进制数，并且结合前缀和的思路，将字符串转换为数值
有几点需要注意的是：
- 一般哈希我们认为会产生冲突，需要解决冲突，但是在字符串哈希中我们一般认定不会产生冲突，所以代码实现上不考虑冲突解决
- 这里说的P进制数一般选取131或者13331，将字符串转换为数值时底数为P
- 哈希会对P进制的数转化成的数值执行取模操作，这是为了将数值压缩到一定空间内，而模数Q一般选取 \(2^64\)
- P和Q之所以这么选择是为了尽可能减少冲突
应用示例1
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5 + 10, M = 1e6 + 10, P = 131;
int n, m;
char tem[N], s[M];
ULL h[M], p[M];
inline ULL gethash(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1];
}
int main()
{
cin >> n >> (tem + 1);
cin >> m >> (s + 1);
// 获得template串hash值
ULL hashcode = 0; // 注意所有的hashcode都应该是对Q(2^64)取模的，即都需要定义为unsigned long long溢出时才会进行取模
for (int i = 1; i <= n; ++ i)
hashcode = hashcode * P + tem[i];
// 获得s串字符串哈希前缀和 + p的各个幂数
p[0] = 1;
for (int i = 1; i <= m; ++ i)
{
p[i] = p[i - 1] * P;
h[i] = h[i - 1] * P + s[i];
}
for (int i = 1; i + n - 1 <= m; ++ i)
if (gethash(i, i + n - 1) == hashcode)
cout << i - 1 << ' ';
return 0;
}
应用实例2
/**
* 字符串哈希的方式：字符串前缀哈希法
* "ABABC"
* 它的前缀分别为
* "A"
* "AB"
* "ABA"
* "ABAB"
* "ABABC"
* 把每一个前缀字符串当作一个P进制数，比如把'A'映射为1，所以"ABA"=(1 * p^2 + 2 * p^1 + 1 * p^0) % Q
* 某个字母不能映射为0，p进制下的0、000、0000转化为10进制后都是一样的，我们必须保证两个字符串的映射值一定不相同才可以区分出来
* 之所以%Q，是因为P进制数转换为10进制数后可能很大
* 因为是mod运算，所以难免会产生冲突，但是在字符串哈希这里，我们的P如果选择131 或者 13331，Q选择2^64，则认为在大多数情况下不会产生冲突，当然这是个玄学问题
*
* 神奇且巧妙的一点是%2^64只需要将所有数据类型都定义为unsigned long long即可自动完成取模，因为无符号数溢出相当于取模，而unsigned long long最大为2^64-1，也就是2^64时为0，2^64+1为1，正好是取模的结果
*/
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
const int N = 1e5 + 10, P = 131; // 也可以选择P = 13331
int n, m;
char str[N];
ULL h[N], p[N]; // 因为题目涉及到多次查询，每次都跑一边快速幂太耗时了，所以p数组把p的幂预处理一下
inline ULL get(int l, int r)
{
return h[r] - h[l - 1] * p[r - l + 1]; // 按理说这里
}
int main()
{
cin >> n >> m;
cin >> str + 1;
p[0] = 1;
for (int i = 1; i <= n; ++ i)
{
p[i] = p[i - 1] * P;
h[i] = h[i - 1] * P + (str[i] - 'a' + 1); // 这里的str[i] - 'a' + 1直接用str[i]也是对的，因为我们最开始就说了默认这个哈希不会产生冲突，所以只要字母的映射值不一样即可，至于是映射为1之类的还是映射为ASCII码无所谓
}
while (m --)
{
int l1, r1, l2, r2;
cin >> l1 >> r1 >> l2 >> r2;
if (get(l1, r1) == get(l2, r2)) cout << "Yes" << endl;
else cout << "No" << endl;
}
return 0;
}
