【刷题】洛谷 P4142 洞穴遇险

题目背景

ZRQ在洞穴中准备采集矿物的时候遇险了！洞穴要塌了！

题目来源：zhoutb2333

题目描述

整个洞穴是一个 \(N*N\) 的方格图，每个格子形如 \((X,Y),1 \le X,Y \le N\) 。其中 \(X\) 表示从上到下的行数，\(Y\) 表示从左到右的列数。 \((1,1)\) 在左上角，\((1,N)\) 在右上角， \((N,1)\) 在左下角， \((N,N)\) 在右下角。

满足 \(X+Y\) 为奇数格子的有一个不稳定度 \(V_{X,Y}\) ， \(X+Y\) 为偶数的格子的不稳定度为 \(0\) 。

ZRQ现在手里恰巧有 \(M\) 个可以支撑洞穴的柱子，柱子的力量可以认为是无穷大。

只要支撑住了一个格子那么这个格子的不稳定度将降为 \(0\) 。

每个柱子是 \(L\) 型的，它除了要占据当前的格子外，还需要占据两个相邻的格子（这三个格子形成 \(L\) 型,可以选择任意方向放置，一共有 \(4\) 个方向）。

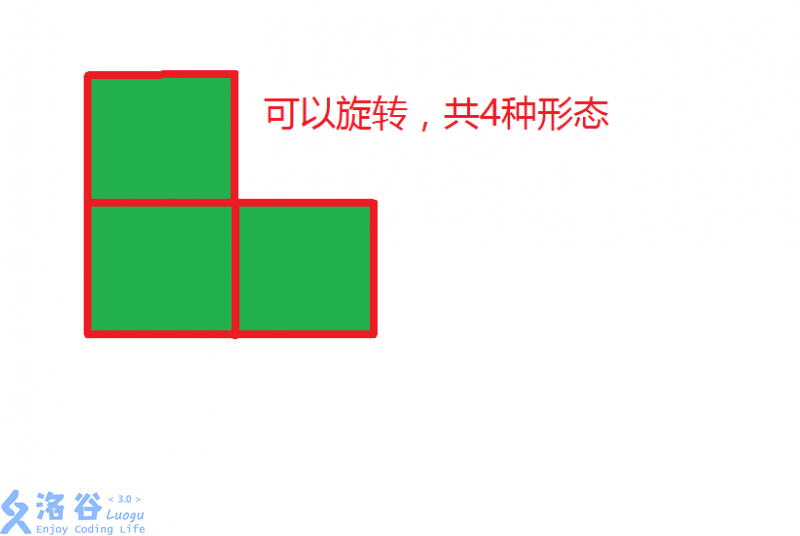
柱子占据相邻的格子不会降低其不稳定度（换句话说就是柱子只有在拐角处有力量）。

有些格子的顶已经塌下来了，无法在其位置放置柱子了，这些格子也不能被占据了。这样已经塌了的格子有 \(K\) 个（他们的不稳定度都为 \(0\) ，即使 \(X+Y\) 为奇数，塌下来的格子的不稳定度也会为 \(0\) ）。

ZRQ想问你，在放置一些柱子后 ，最小的不稳定度之和为多少（可以不将 \(M\) 个柱子都放完）。

输入输出格式

输入格式：

第一行三个整数 \(N,M,K\)

接下来 \(N\) 行每行 \(N\) 个整数，表示每个格子的不稳定度，保证 \(X+Y\) 为偶数的格子和已经塌下的格子的不稳定度为 \(0\) 。

接下来 \(K\) 行每行 \(2\) 个整数 \(X,Y\) ，表示已经塌下的格子的坐标。

输出格式：

一行一个整数，表示最小的不稳定度的和。

输入输出样例

输入样例#1：

3 3 1
0 1 0
2 0 1
0 1 0
1 3

输出样例#1：

3

输入样例#2：

3 3 4
0 2 0
0 0 4
0 3 0
1 3
2 1
2 2
3 1

输出样例#2：

9

说明

共 \(10\) 个测试点，每个点 \(10\) 分，计 \(100\) 分。

对于测试点 \(1\) ~ \(3\) ，有 \(1 \le N \le 6\)

对于测试点 \(4\) ~ \(7\) ，有 \(1 \le N \le 11\)

对于测试点 \(8\) ~ \(10\) ，有 \(1 \le N \le 50\)

对于所有测试点， \(0 \le M \le \frac{N^2}{3}, 0 \le K \le N^2, 0 \le V_{X,Y} \le 10^6\)

样例#1解释：

显然无法让任意两个不稳定的格子都被拐角覆盖，于是将 \((2,1)\) 用拐角覆盖住即可。这样剩余的不稳定度为 \(V_{1,2}+V_{2,3}+V_{3,2}=1+1+1=3\) 。

样例#2解释：

一个都放不下，这样剩余的不稳定度为 \(V_{1,2}+V_{2,3}+V_{3,2}=2+4+3=9\) 。

题解

考虑费用流。
为了方便描述，偶数格表示的是 为偶数的格子，奇数格表示的是为奇数的格子。
首先拐⻆处肯定放在有危险度的格子上。然后可以把这个 'L' 形石头看做是一条从奇数列的偶数格到奇数格再到偶数列的偶数格的一条路径。于是建四列点，把奇数列的偶数格放在第一列，每个奇数格拆成两个点分别放在第二列和第三列，偶数列的偶数格放在第四列。第一列到第二列是如果点是相邻的则连容量为 \(1\) 费用为 \(0\) 的边，第三列到第四列同理,第二列到第三列的相同点则连容量为 \(1\) 费用为负的危险度的边，然后源点向第一列，第四列向汇点连容量为 \(1\) 费用为 \(0\) 的边。
然后跑最小费用最大流，当此次增广的费用是正的了或者增广了次时就break，因为可能根本就放不下个石头，后面增广的费用是为了得到最大流而退流形成的，并不需要石头越多越好，我们只希望费用最小。

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=100+10,MAXM=50000+10,inf=0x3f3f3f3f;
int n,m,k,e=1,beg[MAXN*MAXN*2],nex[MAXM<<1],to[MAXM<<1],cap[MAXM<<1],was[MAXM<<1],ans,G[MAXN][MAXN],T[MAXN][MAXN],prex[MAXN*MAXN*2],s,t,pres[MAXN*MAXN*2],M[4][MAXN][MAXN],tot,p[MAXN*MAXN*2],level[MAXN*MAXN*2];
std::queue<int> q;
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void insert(int x,int y,int z,int w)
{
	to[++e]=y;
	nex[e]=beg[x];
	beg[x]=e;
	cap[e]=z;
	was[e]=w;
	to[++e]=x;
	nex[e]=beg[y];
	beg[y]=e;
	cap[e]=0;
	was[e]=-w;
}
inline bool bfs()
{
	memset(level,inf,sizeof(level));
	level[s]=0;
	p[s]=1;
	q.push(s);
	while(!q.empty())
	{
		int x=q.front();
		q.pop();
		p[x]=0;
		for(register int i=beg[x];i;i=nex[i])
			if(cap[i]&&level[to[i]]>level[x]+was[i])
			{
				level[to[i]]=level[x]+was[i];
				if(!p[to[i]])p[to[i]]=1,q.push(to[i]);
				prex[to[i]]=x;
				pres[to[i]]=i;
			}
	}
	return level[t]<0;
}
inline void dfs()
{
	int f=inf;
	for(register int i=t;i!=s;i=prex[i])chkmin(f,cap[pres[i]]);
	for(register int i=t;i!=s;i=prex[i])ans+=f*was[pres[i]],cap[pres[i]]-=f,cap[pres[i]^1]+=f;
}
int main()
{
	read(n);read(m);read(k);
	for(register int i=1;i<=n;++i)
		for(register int j=1;j<=n;++j)read(G[i][j]),ans+=G[i][j];
	for(register int i=1;i<=k;++i)
	{
		int x,y;read(x);read(y);
		T[x][y]=1;
	}
	for(register int i=1;i<=n;++i)
		for(register int j=1;j<=n;++j)
			if((i+j)&1)
			{
				M[1][i][j]=++tot,M[2][i][j]=++tot;
				if(!T[i][j])insert(M[1][i][j],M[2][i][j],1,-G[i][j]);
			}
			else M[((i&1)?0:3)][i][j]=++tot;
	s=++tot,t=++tot;
	for(register int i=1;i<=n;++i)
		for(register int j=1;j<=n;++j)
			if(T[i][j])continue;
			else if((i+j)&1^1)
			{
				if(i&1)
				{
					if(j!=1&&!T[i][j-1])insert(M[0][i][j],M[1][i][j-1],1,0);
					if(j!=n&&!T[i][j+1])insert(M[0][i][j],M[1][i][j+1],1,0);
					if(i!=1&&!T[i-1][j])insert(M[0][i][j],M[1][i-1][j],1,0);
					if(i!=n&&!T[i+1][j])insert(M[0][i][j],M[1][i+1][j],1,0);
					insert(s,M[0][i][j],1,0);
				}
				else
				{
					if(j!=1&&!T[i][j-1])insert(M[2][i][j-1],M[3][i][j],1,0);
					if(j!=n&&!T[i][j+1])insert(M[2][i][j+1],M[3][i][j],1,0);
					if(i!=1&&!T[i-1][j])insert(M[2][i-1][j],M[3][i][j],1,0);
					if(i!=n&&!T[i+1][j])insert(M[2][i+1][j],M[3][i][j],1,0);
					insert(M[3][i][j],t,1,0);
				}
			}
	while(bfs()&&m--)dfs();
	write(ans,'\n');
	return 0;
}