【刷题】BZOJ 4827 [Hnoi2017]礼物

Description

我的室友最近喜欢上了一个可爱的小女生。马上就要到她的生日了，他决定买一对情侣手 环，一个留给自己，一个送给她。每个手环上各有 n 个装饰物，并且每个装饰物都有一定的亮度。但是在她生日的前一天，我的室友突然发现他好像拿错了一个手环，而且已经没时间去更换它了！他只能使用一种特殊的方法，将其中一个手环中所有装饰物的亮度增加一个相同的自然数 c（即非负整数）。并且由于这个手环是一个圆，可以以任意的角度旋转它，但是由于上面 装饰物的方向是固定的，所以手环不能翻转。需要在经过亮度改造和旋转之后，使得两个手环的差异值最小。在将两个手环旋转且装饰物对齐了之后，从对齐的某个位置开始逆时针方向对装饰物编号 1,2,…,n，其中 n 为每个手环的装饰物个数，第 1 个手环的 i 号位置装饰物亮度为 xi，第 2 个手 环的 i 号位置装饰物亮度为 yi，两个手环之间的差异值为(参见输入输出样例和样例解释)： \sum_{i=1}^{n}(x_i-y_i)2麻烦你帮他计算一下，进行调整（亮度改造和旋转），使得两个手环之间的差异值最小， 这个最小值是多少呢？

Input

输入数据的第一行有两个数n, m，代表每条手环的装饰物的数量为n，每个装饰物的初始 亮度小于等于m。

接下来两行，每行各有n个数，分别代表第一条手环和第二条手环上从某个位置开始逆时 针方向上各装饰物的亮度。

1≤n≤50000, 1≤m≤100, 1≤ai≤m

Output

输出一个数，表示两个手环能产生的最小差异值。

注意在将手环改造之后，装饰物的亮度 可以大于 m。

Sample Input

5 6
1 2 3 4 5
6 3 3 4 5

Sample Output

1
【样例解释】
需要将第一个手环的亮度增加1，第一个手环的亮度变为： 2 3 4 5 6 旋转一下第二个手环。对于该样例，是将第
二个手环的亮度6 3 3 4 5向左循环移动 2017-04-15 第 6 页，共 6 页 一个位置，使得第二手环的最终的亮度为
：3 3 4 5 6。 此时两个手环的亮度差异值为1。

Solution

可以变换位置，也可以同时加数
假设确定了两个序列的位置，那么答案就是 \(\sum_{i=0}^{n-1}(xi-yi+c)^2\)
拆开， \(\sum_{i=0}^{n-1}x_i^2+y_i^2+c^2-2x_iy_i+2x_ic-2y_ic\)

\(~~~~(\sum_{i=0}^{n-1}x_i^2+y_i^2)+(\sum_{i=0}^{n-1}c^2+2c(x_i-y_i))-2(\sum_{i=0}^{n-1}x_iy_i)\)
\(=[(\sum_{i=0}^{n-1}x_i^2)+(\sum_{i=0}^{n-1}y_i^2)]+[nc^2+2((\sum_{i=0}^{n-1}x_i)-(\sum_{i=0}^{n-1}y_i))c]-2[\sum_{i=0}^{n-1}x_iy_i]\)

然后，第一部分就是求和，第二部分可以发现是个系数确定的二次函数，要最小肯定是取最值
也就是说，对于每一种不同的序列的排列，有两项的值是一直不变的。那么我们只要算第三部分，找排列使第三部分的值最小，那么就会使最终答案最小
其实把 \(y\) 数组翻转一下，就会发现它其实就是个FFT
假设两个数组是这样对应的

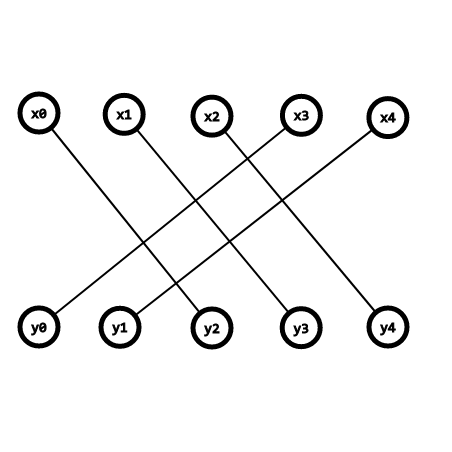
那么 \(y\) 数组翻转之后变成了这样

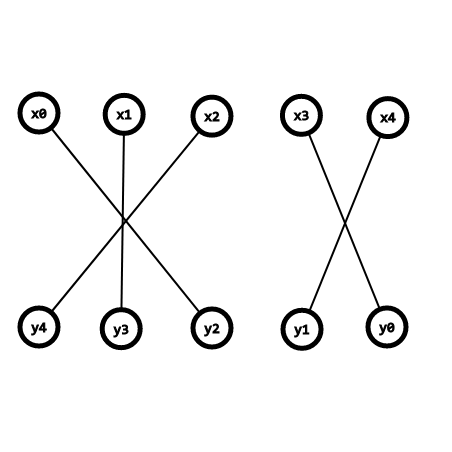
变成了两个交叉部分，而这两个部分对应的形式不就是FFT的形式吗
于是就枚举两个部分的分界点，将两个FFT加起来就是一种对应方案的第三部分的答案
对所有方案取min就好了
注意的一点是，在求二次函数的最值的时候，因为数列同时加数必须是自然数，小数不行，那么就不能直接用最值公式去得到最值，必须得到两个最接近对称轴的整数点，用它们求函数值取min

#include<bits/stdc++.h>
#define ui unsigned int
#define ll long long
#define db double
#define ld long double
#define ull unsigned long long
const int MAXN=1<<17,inf=0x3f3f3f3f;
const db Pi=acos(-1.0);
int qn,n,m,rev[MAXN],G[MAXN],ans=inf,xs,ys,xs2,ys2,cnt,x1,x2,ext;
struct Complex{
	db real,imag;
	inline Complex operator + (const Complex &A) const {
		return (Complex){real+A.real,imag+A.imag};
	};
	inline Complex operator - (const Complex &A) const {
		return (Complex){real-A.real,imag-A.imag};
	};
	inline Complex operator * (const Complex &A) const {
		return (Complex){real*A.real-imag*A.imag,imag*A.real+real*A.imag};
	};
};
Complex x[MAXN],y[MAXN];
template<typename T> inline void read(T &x)
{
	T data=0,w=1;
	char ch=0;
	while(ch!='-'&&(ch<'0'||ch>'9'))ch=getchar();
	if(ch=='-')w=-1,ch=getchar();
	while(ch>='0'&&ch<='9')data=((T)data<<3)+((T)data<<1)+(ch^'0'),ch=getchar();
	x=data*w;
}
template<typename T> inline void write(T x,char ch='\0')
{
	if(x<0)putchar('-'),x=-x;
	if(x>9)write(x/10);
	putchar(x%10+'0');
	if(ch!='\0')putchar(ch);
}
template<typename T> inline void chkmin(T &x,T y){x=(y<x?y:x);}
template<typename T> inline void chkmax(T &x,T y){x=(y>x?y:x);}
template<typename T> inline T min(T x,T y){return x<y?x:y;}
template<typename T> inline T max(T x,T y){return x>y?x:y;}
inline void FFT(Complex *A,int tp)
{
	for(register int i=0;i<n;++i)
		if(i<rev[i])std::swap(A[i],A[rev[i]]);
	for(register int l=2;l<=n;l<<=1)
	{
		Complex wn=(Complex){cos(2*Pi/l),sin(tp*2*Pi/l)};
		for(register int i=0;i<n;i+=l)
		{
			Complex w=(Complex){1,0};
			for(register int j=0;j<(l>>1);++j)
			{
				Complex A1=A[i+j],A2=A[i+j+(l>>1)]*w;
				A[i+j]=A1+A2,A[i+j+(l>>1)]=A1-A2;
				w=w*wn;
			}
		}
	}
}
int main()
{
	read(qn);read(m);
	for(register int i=0;i<qn;++i)
	{
		int k;read(k);
		x[i].real=(db)k,xs+=k,xs2+=k*k;
	}
	for(register int i=0;i<qn;++i)
	{
		int k;read(k);
		y[qn-i-1].real=(db)k,ys+=k,ys2+=k*k;
	}
	m=qn+qn-1;
	for(n=1;n<m;n<<=1)cnt++;
	for(register int i=0;i<n;++i)rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
	FFT(x,1);FFT(y,1);
	for(register int i=0;i<n;++i)x[i]=x[i]*y[i];
	FFT(x,-1);
	for(register int i=0;i<n;++i)G[i]=(int)(x[i].real/n+0.5);
	chkmin(ans,-2*G[qn-1]);
	for(register int i=0;i<qn;++i)chkmin(ans,-2*(G[i]+G[i+qn]));
	x1=ceil((db)-(xs-ys)/qn),x2=floor((db)-(xs-ys)/qn);
	ext=min(qn*x1*x1+2*(xs-ys)*x1,qn*x2*x2+2*(xs-ys)*x2);
	write(ans+xs2+ys2+ext,'\n');
	return 0;
}