1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
答:
1.
本节重点知识点是线性回归算法,它属于监督学习的一种,是评估自变量X与因变量Y之间的一种线性关系。当只有一个自变量的时候,称为一元线性回归,当具有多个自变量的时候, 称为多元线性回归。通俗的讲,就是将真实的数据,映射到坐标轴中,这些数据在坐标轴中,呈现偏向线状的形状,然后构建一个函数,需要最优解,并用来预测结果,如下图呈线性相关关系。
2.线性回归算法可以用来预测结果,例如根据电脑的价格可以线性回归出电脑的配置,预测买到电脑的配置,或者在自动驾驶碰到障碍物的时候,根据障碍物的大小预测轮子需要转动的角度是多少等等。
3.
截图如下:
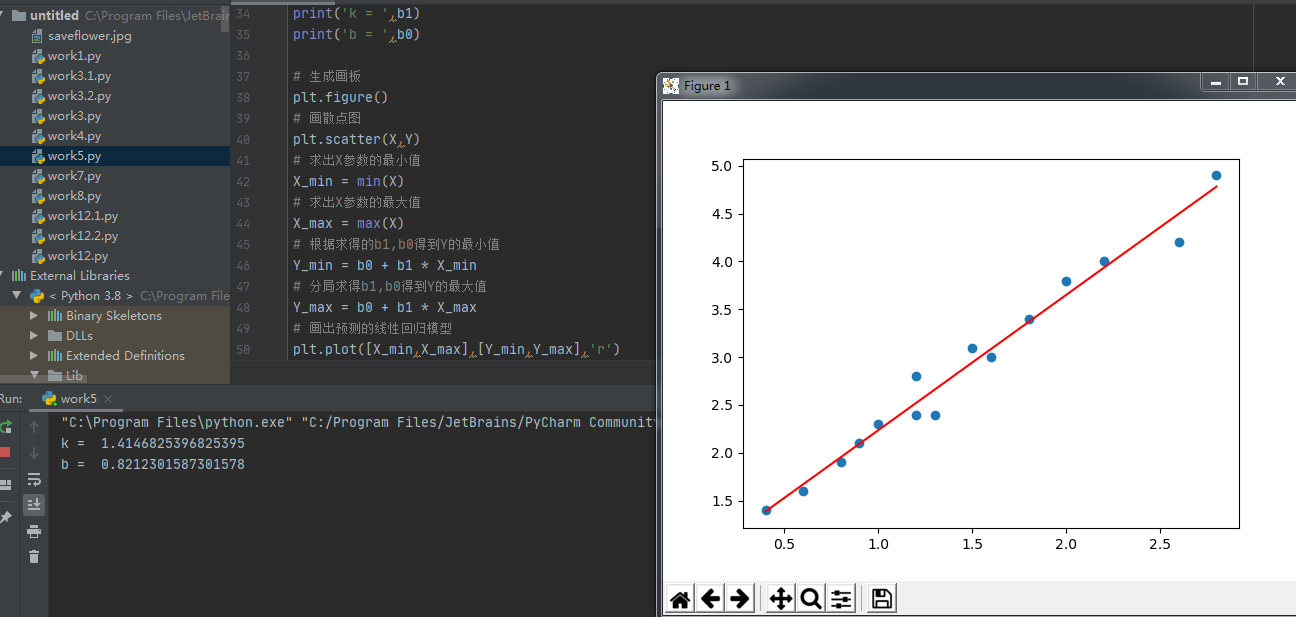
代码如下:
import numpy as np
from matplotlib import pyplot as plt
def F(X,Y):
X_avg = np.mean(X)
Y_avg = np.mean(Y)
n = len(X)
# 定义分子和分母
fen_zi = 0
fen_mu = 0
for i in range(0,n):
fen_zi += (X[i] - X_avg) * (Y[i] - Y_avg)
fen_mu += (X[i] - X_avg) ** 2
b1 = fen_zi / float(fen_mu)
b0 = Y_avg - X_avg * b1
return b0,b1
def predict(x,b0,b1):
return b0 + x * b1
X=[1.5,0.8,2.6,1.0,0.6,2.8,1.2,0.9,0.4,1.3,1.2,2.0,1.6,1.8,2.2]
Y=[3.1,1.9,4.2,2.3,1.6,4.9,2.8,2.1,1.4,2.4,2.4,3.8,3.0,3.4,4.0]
b0,b1 = F(X,Y)
print('k = ',b1)
print('b = ',b0)
# 生成画板
plt.figure()
# 画散点图
plt.scatter(X,Y)
# 求出X参数的最小值
X_min = min(X)
# 求出X参数的最大值
X_max = max(X)
# 根据求得的b1,b0得到Y的最小值
Y_min = b0 + b1 * X_min
# 分局求得b1,b0得到Y的最大值
Y_max = b0 + b1 * X_max
# 画出预测的线性回归模型
plt.plot([X_min,X_max],[Y_min,Y_max],'r')
# 展示最终的效果
plt.show()



