Plucker坐标的新理解

Plucker坐标表示的是6自由度的，在表示变换和重投影时具有良好的现行特性。假设直线上两个点的坐标分别为 \({A^T}\)、\({B^T}\)
那么Plucker矩阵可以表示为：\({L=AB^T-BA^T}\)
假设 \({A^T=(x_1,y_1,z_1,w_1)、B^T={(x_2,y_2,z_2,w_2)}}\) 那么有：

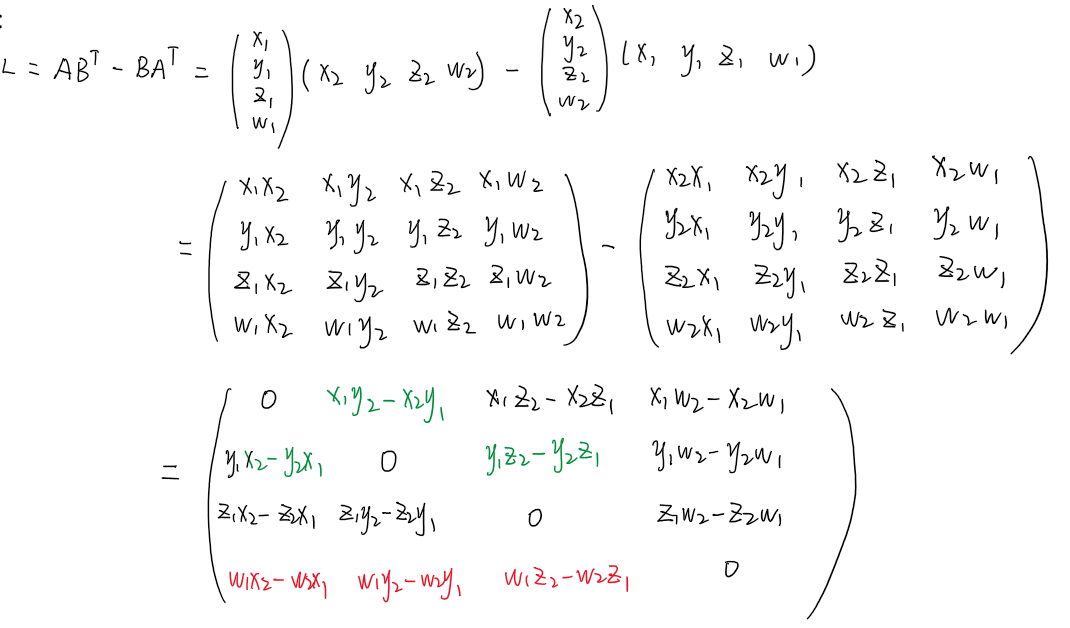
可以发现该矩阵是一个反对称矩阵--> \({l_{ii}=0,l_{ij}=-l_{ji}}\)
现在将红色部分定义为n，将绿色部分定义为v，有：\({n=[l_{41},l_{42},l_{43} ]^T,v=[l_{23},l_{31},l_{12} ]^T}\)
这意味着n表示方向向量，v表示法向量（穿过原点和直线），与方向向量垂直，满足 \({n^T v=0}\)
假设w=1，表示齐次坐标，有:
\({X_2 - X_1 =n}、{X_1 × X_2 =v}\)

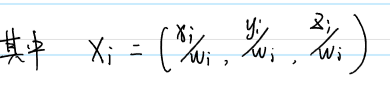
Plucker矩阵L与Plucker坐标\({L=(n,v)^T}\) 的转换关系如下:

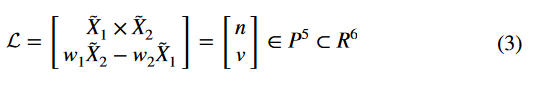
使用 Plucker坐标表示空间中的直线有很多优点。尤其是在表示坐标系转换和相机重投影时，具有线性形式。例如，当世界坐标系和相机坐标系进行转换时，可以表示为

---