左式堆

注：这里的堆还是以小根堆为例。

 

我们想要设计一种堆能像二叉堆那样高效地支持合并操作，也就是$O\left( n \right)$时间处理一次Merge，而且只使用一个数组看起来很困难对吧，毕竟合并操作需要把一个数组复制到另外一个数组中去，对于相同大小的堆这会花费$\theta \left( n \right)$。也正因如此，我们可以看到，在此前所有支持高效合并的高级数据结构都需要用到指针。但是！在实践中就有一些问题，它会使操作效率变低，因为处理指针一般而言比乘除法操作更耗费时间。

那该怎么做呢？二叉堆进化——左式堆，又叫左偏树。像二叉堆那样，左式堆也具有结构特性和有序性，有着和二叉堆相同的heap property。他和二叉堆的唯一区别是：左式堆不是理想平衡的，而是趋向于极其不平衡，在拓扑形态上更倾向于向左倾斜的。那么，为什么要引入这一新的变种呢？让我们从它的设计动机以及结构定义说起。前面说了，我们的目的是完成高效合并，现有的很多方法已经足够合并了，但是太慢。而数据结构的精髓就是不断优化性能，所以需要引入新的结构来完成这个目的。下面先来逐一分析各种拍脑袋的算法，然后逐渐逼近这次的主角。

最平凡的思路是以大的为基础，把小的堆里元素逐一取出插入到A中，B为空时就完成了。

可以一句话概括：Insert（DeleteMax（B），A）;

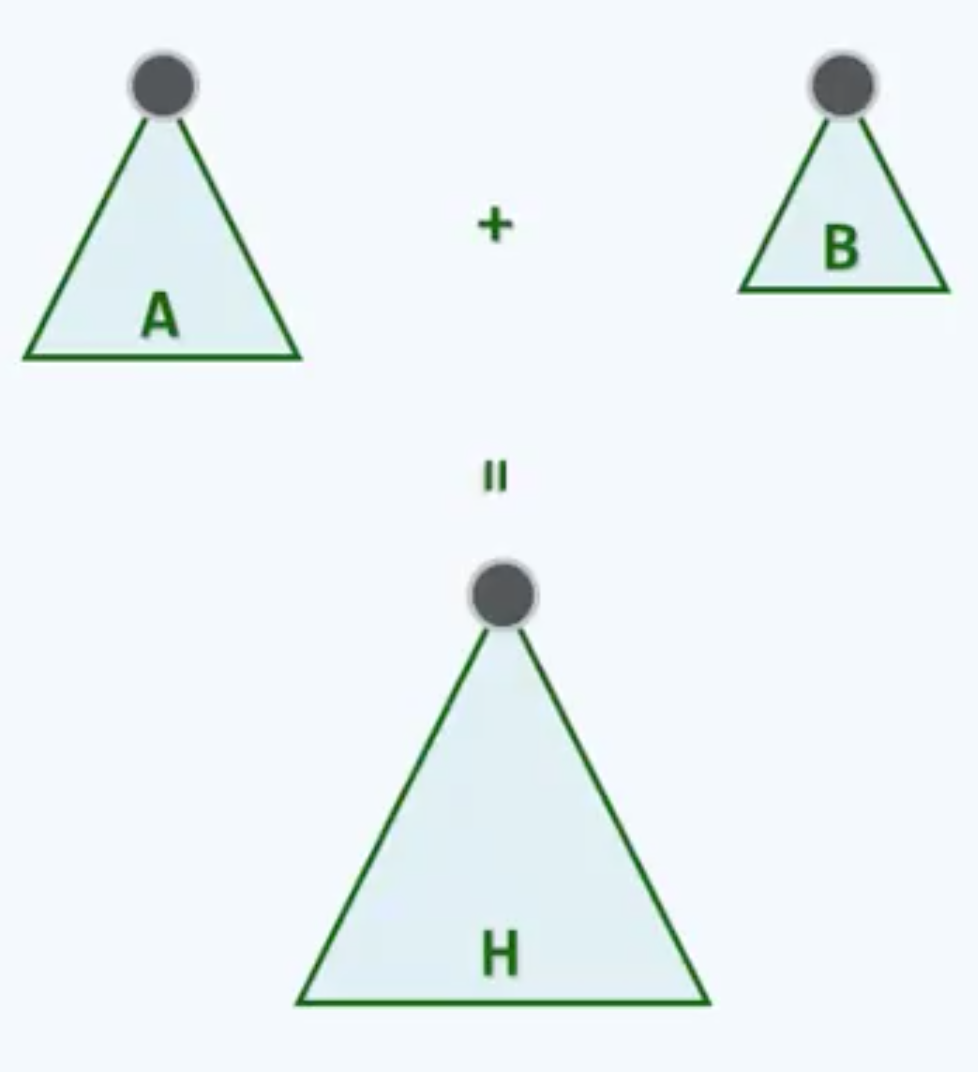
但这太慢了，简直龟速。分析一下，我们把两个堆的规模记作n和m，不失一般性地，假设A不小于B，也就是：$\left| A \right|\; =\; n\; \; \geq \; m\; =\; \left| B \right|$。所以整个算法迭代$m$次，在每一次里deleteMax(B)要花费$\log m$的时间，把这个元素汇入A中花费$\log \left( n\; +\; m \right)$的时间。所以一共是$O\left( \; m\; \cdot \; \left( \log m\; +\; \log \left( n\; +\; m \right) \right) \right)\; =\; O\left( m\; \cdot \; \log \left( n\; +\; m \right) \right)\; =\; O\left( m\cdot \; \log n \right)$的时间。恐怕你自己恐怕都不满足这个效率，因为的确有改进的空间。我们会再想起Floyd批量建堆算法，嗯没错，更高效的办法是先把两个堆混合起来，然后通过下滤，维护整个堆的结构特性，把它整理为一个完全二叉堆。概括一下就是BuildHeap(n+m, union(A,B));而Floyd算法只需要线性时间，也就是总共$O\left( n\; +\; m \right)$，这个效率就高一些了。

 

但这还不能令人满意，原因在于：Floyd算法的输入默认是无序的，而我们的两堆分别都是有序的，刚才这个算法没有利用到我们已知的信息，如果利用上了这部分有序的信息，就可以加速执行了。从这个角度出发，我们有理由相信：一定存在更高效的数据结构和相应算法。的确如此，Clark Allan Crane历经探索，发明了一个新的结构：左式堆，并于1972年以此发表了他的博士论文$Linear\; Lists\; and\; Priority\; Queues\; as\; Balanced\; \mbox{Bi}nary\; T\mbox{re}es$。这种结构在保持堆序的前提下附加少量条件，就能在合并过程中只需要调整很少的节点，插入和删除都仅需要$O\left( \log n \right)$的时间。比刚才的$O\left( n\cdot \log n \right)$和$O\left( n \right)$都有了长足的进步。他的这个新条件就是“单侧倾斜”，节点分布都偏向左侧，而算法高效的诀窍是合并操作只涉及右侧，而右侧节点很少。

 

比如这就是左式堆的典型图解，左长右短，它可以把右侧节点严格控制在$O\left( \log n \right)$以内，这也印证了上面说的合并操作的复杂度在O(logn)范围内。这也引发出一个定理：在右侧路径上有 $r$ 个节点的左式堆必然至少有 $2^{r\; }-\; 1$  个节点。

 

 

 

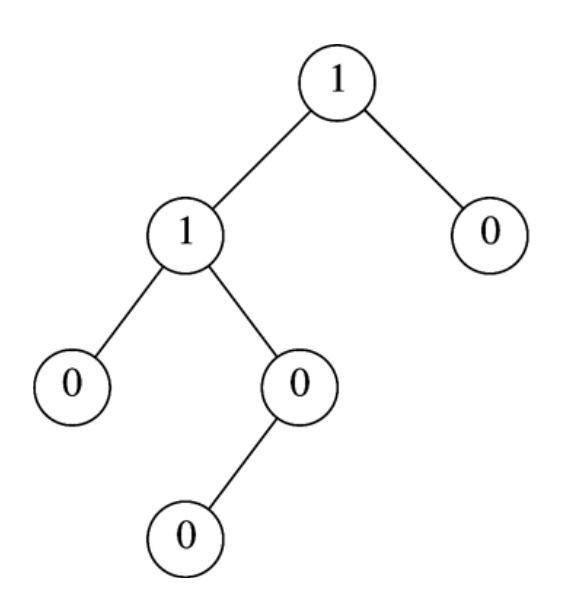
那它是怎么做到这么快的呢？现在讨论这个还为时过早，因为首先要回答另一个问题。前面第三自然段提到过：它不是理想平衡的，而是趋向于极其不平衡。不平衡的话结构性就荡然无存了，但我们需要明白的是：对于Heap，堆序才是本质特征，其他的都无所谓，在必要时刻都可以牺牲掉，毕竟，计算机科学就是一门关于权衡的学问。

现在我们来讨论一下左式堆的性质，引入一个概念：零路径长（null path length,npl）定义为从某个节点X到一个叶子的最短路径长。上图中节点内标示的就是。因此具有0 or 1个儿子的节点的npl是0，定义$npl\; \left( \; null\;  \right)\; =\; -1$。那很自然，对于每个节点的npl有如下计算公式：

$npl\left( \; x\; \right)\; =\; \; 1\; +\; \min \left( \; npl\left( \; lc\; \right)\; ,\; npl\; \left( \; rc\; \right)\; \right)$ 

看上去和某个公式有点眼熟啊，求树高度的算法，和这个很类似，就是把min换成了max,通过类比我们或许对这两个概念能有更深的认识。

有了这个指标，我们就可以以此来度量堆结构的倾斜性。如果左孩子的npl不小于右孩子，就称之为左倾（政治上追求进步2333），如果每个节点都符合这个性质，就称为左倾堆or左式堆。又因为npl定义是在两个孩子中取一个小值+1，那么我们只考虑右边就行了。总结如下：

左倾：对任何节点 $x$，都有$npl\left( \; x->\; lc\;  \right)\; \geq \; npl\left( \; x->rc\;  \right)$

推论：对任何节点 $x$，都有$npl\left( \; x\;  \right)\; =\; 1\; +\; npl\left( \; x->rc\;  \right)$

我们也可以推论：左式堆的任何一个子堆也必然是左式堆。第三自然段说过左式堆倾向于节点向左倾斜，但这只是大致的倾向，实际情况不一定都向左。

下面讨论实现，先说合并，然后是插入和删除。

先说一下类型声明

#ifndef LeftHeap_h
#define LeftHeap_h
struct TreeNode;
typedef struct TreeNode *LefHeap;
LefHeap Init();
int FindMin(LefHeap H);
LefHeap Merge(LefHeap H1,LefHeap H2);

//#define Insert(X,H) (H=Insert1((X),H))
void Insert(int x,LefHeap H);
int DeleteMin(LefHeap H);
LefHeap Insert1(int x,LefHeap H);
LefHeap DeleteMin1(LefHeap H);



#endif /* LeftHeap_h */
struct TreeNode{
    int value;
    LefHeap left;
    LefHeap right;
    int npl;
};

 

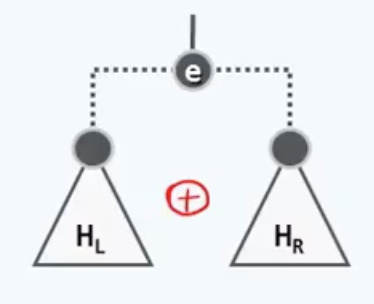
采用递归的模式可以非常简明的描述合并算法，对于一般情形：

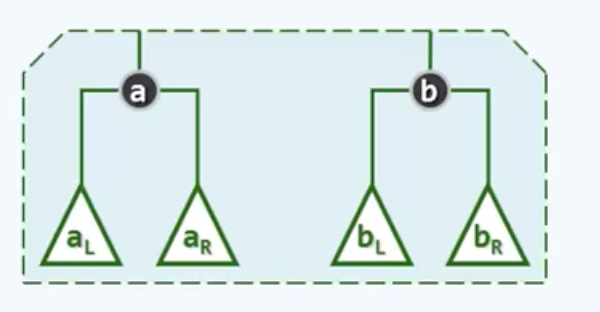
可以借助递归将a、b两个堆合并的问题转化为这样一个问题：

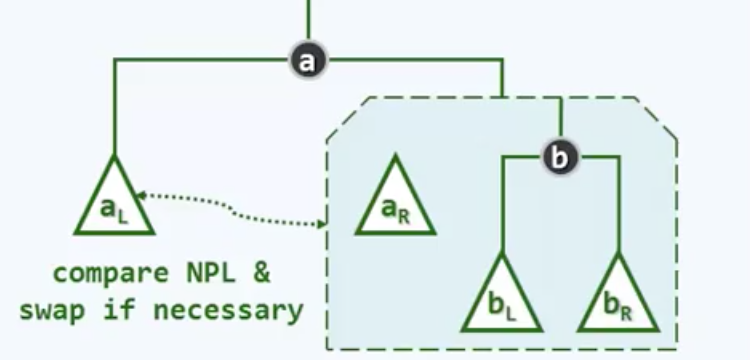
具体来说也就是我们要将a的右子堆取出，并且递归地与刚才的堆b完成合并，合并所得的结果继续作为a的右子堆。当然，为了保证a在此后继续满足左倾性，在这次合并返回之后，我们还须比较a_L与合并之后这个堆的npl值，如果有必要，我们还需令二者互换位置。递归写法如下

void swap(LefHeap h1,LefHeap h2){
    LefHeap temp=h1;
    h1=h2;
    h2=temp;
}
static LefHeap Merge1(LefHeap H1,LefHeap H2);
void SwapChildren(LefHeap H1){
    swap(H1->left, H1->right);
}

LefHeap Merge(LefHeap a,LefHeap b){
    //递归基
    if(!a)
        return b;
    if (!b)
        return a;
    /*执行到这一句之后就说明两个堆都不为空,此时我们要比较两个根节点在数值上的大小，如果有必要应将二者互换名称。从而保证在数值上a总是不小于b，以便在后续递归的过程中将b作为a的后代。
     */
    if (a->value < b->value)
        swap(a, b);  //一般情况下首先确保a更大,然后执行合并
    a->right=Merge(a->right, b);
    //之后我们要保证a的左倾性：
    if(!a->left || a->left->npl < a->right->npl)
        //如果有必要，我们就交换a的左右子堆，以确保右子堆的npl更小
        SwapChildren(a);
    
    //然后更新a的npl
    a->npl=a->right->npl+1;
    return a;//返回合并后的堆顶
}

具体例子如下：

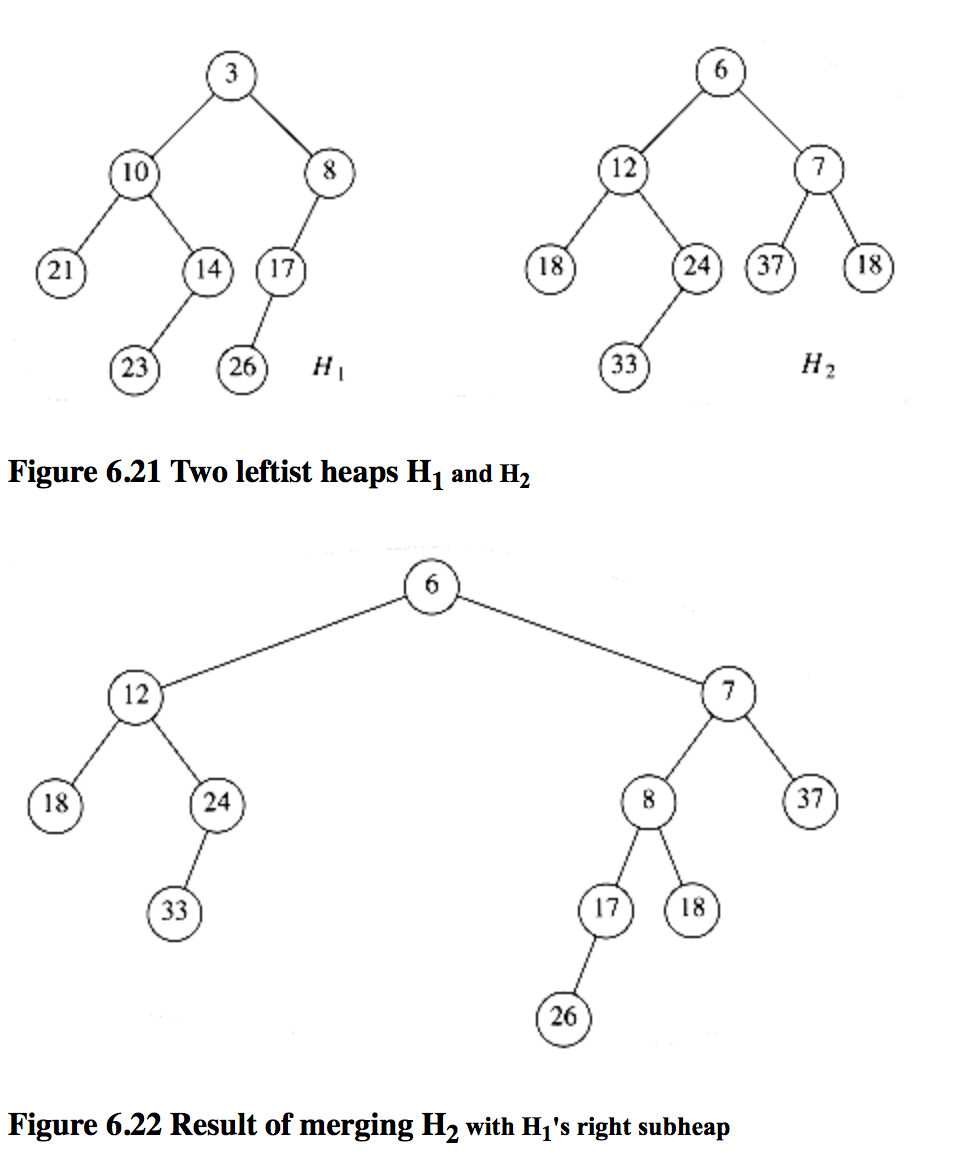
最终：

 

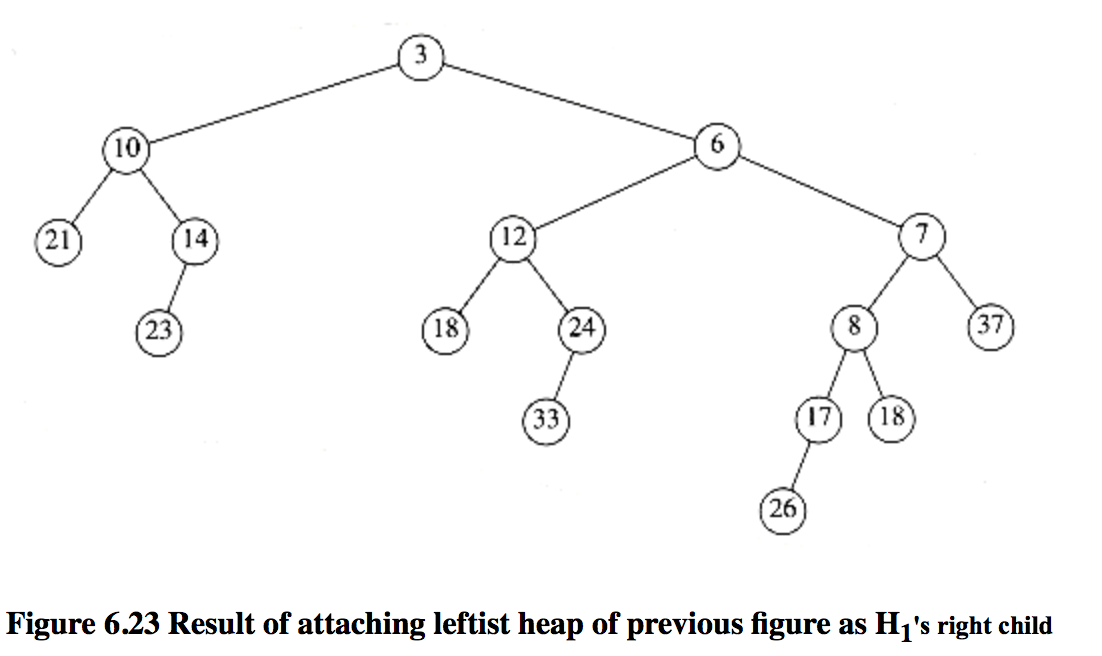
要注意的是，在合并之后，原始的两个堆就别再碰了，因为他们本身的变化会影响合并的结果。执行合并的时间与右侧路径的长度之和成正比，因为在递归期间每一个被访问节点执行的是常数工作量。因此合并的时间界限为$O\left( \log n \right)$，也可以分两趟用非递归的方式来做：第一趟，通过合并2个堆的右路径建立一颗新树。为此我们要以升序（or降序，反正要保持有序）安排a,b右路径上的节点，保持左孩子不变。在这个例子中，新的右路径是3，6，7，8，18。第二趟构成左式堆，在那些性质被破坏的节点上进行交换，交换这些节点的两个孩子。

 

对于插入，可以通过把插入项看作单节点堆并执行一次Merge。

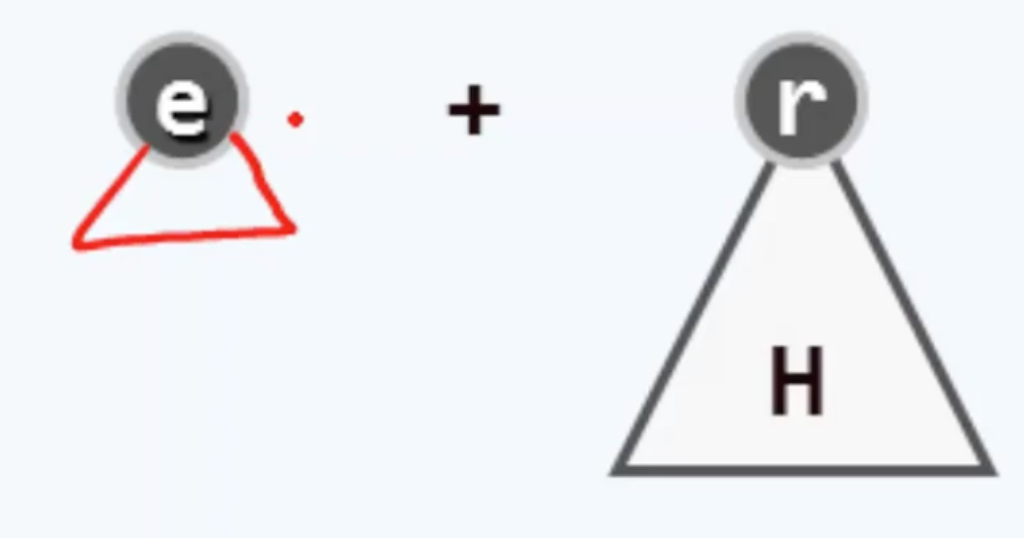
void Insert(int x,LefHeap H){
    LefHeap fresh;
    fresh=malloc(sizeof(struct TreeNode));
    fresh->value=x;
    fresh->npl=0;
    fresh->left=fresh->right=NULL;
    H=Merge(fresh, H);
}

 

删除的话，就是除掉根得到两个堆，然后再合并，因此时间还是$O\left( \log n \right)$ 

int DeleteMin(LefHeap H){
    LefHeap l=H->left;
    LefHeap r=H->right;
    int t=H->value;//前三句都是铺垫，对相关的数据作备份而已。
    free(H);//根节点的物理摘除由这一句来完成。
    //此后只需将此时被隔离开的左子堆与右子堆重新地合并起来。
    H=Merge(l, r);
    return t;
}

可以看到，按照这一方式，无论是左式堆的删除还是刚才的插入操作，实质的计算无非都集中在合并接口上。此前介绍过，合并可以高效率地在$O\left( \log n \right)$的时间内完成，那如此实现的删除以及刚才实现的插入操作也能达到这样的计算效率。同样的计算效率，更为简明的实现方法，我们还有什么理由不采用这种方式呢？

实际上关于分合之道，左式堆的发明者Crane堪称个中高手。除了左式堆，他还针对其它的许多数据结构给出了高效的合并算法。比如对于我们已经熟悉的AVL树，Crane也给出了一个高效的合并算法，有兴趣不妨找找相关文章。

 

下一篇文章讨论二项队列，与以往不同的是，它并非是一颗堆序的树，而是森林。

p.s. 这段时间要备考托福，所以下篇文章大概会在11月左右发。