开放定址法——平方探测(Quadratic Probing)
为了消除一次聚集,我们使用一种新的方法:平方探测法。顾名思义就是冲突函数F(i)是二次函数的探测方法。通常会选择f(i)=i2。和上次一样,把{89,18,49,58,69}插入到一个散列表中,这次用平方探测看看效果,再复习一下探测规则:hi(x)= ( Hash(x) + F(I) ) % TableSize(I=0,1,2…)
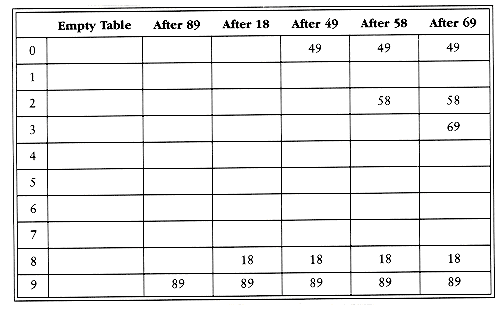
脑内调试一下:49和89冲突时,下一个空闲位置是0号单元。58和18冲突时,i=1也冲突,再试i=2,h2(58)=(8+4)%10=2是空的可以放。69同理。
对于线性探测法而言,我们得避免元素几乎填满的情况,因为这时候性能会急剧降低。对于平方探测法,这会更糟:如果表超过一半被填满,那当表的规模不是素数时,甚至在表被填满一般之前就已经不能一下找到空单元了,需要试探好几次才能找到一个空单元。原因是表最多有一半位置可以用来解决冲突。凭什么如此断言呢?Talk is cheap,show me your….proof.
定理
如果使用平方探测,且表的规模是素数,那么当表至少有一半是空的时候,总能插入新的元素。
我们假设表的Size是一个大于3的素数,直接拿着定理证明有点让人不知所措,那把这个定理的证明转化为:证明“前$\frac{\mbox{Si}ze}{2}$个备选位置是互异的”,然后用反证法。从所有前$\frac{\mbox{Si}ze}{2}$个的位置里选两个:( h(x) + i2 )%Size和( h(x) + j2 )%Size,其中 0 < i,j$ \leq \frac{\mbox{Si}ze}{2}$。假设这两个位置相同,且i ≠ j,然后让他们位置相等,推出矛盾就行了,因为都mod Size,根据等式性质我们只需要考察括号里的项就行了。
(h(x) + i2)=(h(x) + j2)
=> i2 = j2
=> (i-j)(i+j) = 0
前面说了i ≠ j,所以只可能i = - j。但是这和他们的定义域矛盾,所以也是不可能的。所以前一半位置互异,可供选择,任何元素都有$\frac{\mbox{Si}ze}{2}$个可能被放的位置。综上,如果最多有一半的位置可用,那么空闲单元总是能找到的。反过来讲,哪怕表里有一半+1个位置被填上,那么插入都有可能失败(虽然这比较偶然,但还是有可能的),这一点是十分重要的,要拿小本本记下来,说不定校招或考研就出题了哈哈哈。另外保证Size是素数也是非常重要的,如果不是的话,那遭遇冲突时可供选择的空单元个数会锐减到你难以置信的地步,远比一半少,这样一来,我们的战略纵深就太小了,难以迂回,这种情况没人希望见到。

Size=16的时候,找备选的单元只能取i=1,2,3,也就是距离冲突单元1,4,9个单位的位置了。
另外,在开放定址的散列表里,我们之前意义上的删除操作是不能进行的,因为某个数对应的单元可能已经引起过冲突了,然后他探测跑到别的位置了。比如我们要删除69,你find一下,定位到9,发现那躺着89,那我们只能跟着平方探测的思路再找找9+12,结果发现还不对,在那的是58。得,继续找吧,试试9+2^2,这才找到。想想吧,这才Size=10就这么费劲了,那企业级软件要处理千万级甚至亿级的数据怎么办,比如头条app的数据量,那程序还不跑到天荒地老。。。因此开放定址散列表需要懒惰删除。
谈谈怎么实现吧,先给出类型声明。在这里我们不用结构体数组,而使用散列表单元的数组,而且单元是动态分配地址这和分离链接一样。
#ifndef HashQuad_h #define HashQuad_h typedef unsigned int Index; typedef Index Position; struct HashTb1; typedef struct HashTb1 *HashTable; HashTable Init(int size); void DestroyTable(HashTable H); void Insert(int key, HashTable H); Position Find(int key,HashTable H); int Retrieve(Position P); HashTable ReTable(HashTable H); #endif /* HashQuad_h */ enum KindOfEntry{ Legitimate, Empty, Deleted }; struct HashEntry { int value; enum KindOfEntry Info; }; typedef struct HashEntry Cell; /*Cell *TheCells will be an array of HashEntry cells,allocated later */ struct HashTb1 { int TableSize; Cell *TheCells; };
顺便一说,Hash函数还是设置为简单的%Size
Index Hash(int key,int size) { return key%size; }
初始化由2步组成:分配空间,然后将每个单元的Info设置为Empty。
#define aPrime 307 #define MinTableSize 5 HashTable Initial(int size){ HashTable H; int i; if (size<MinTableSize) { printf("Table size too small\n"); return NULL; } //Allocate table H=(HashTable)malloc(sizeof(struct HashTb1)); H->TableSize=aPrime; //Allocate array of cells H->TheCells=(Cell*)malloc(sizeof(Cell)*H->TableSize); //Allocate list headers for (i=0; i<H->TableSize; i++) H->TheCells[i].Info=Empty;
return H; }
和分离链接一样,Find返回key在散列表里的单元号码。而且因为被标记了Empty,我们想表达查找失败也很容易。
1 Position Find(int key,HashTable H){ 2 Position cur; 3 int CollisionNum=0; 4 cur=Hash(key,H->TableSize); 5 while (H->TheCells[cur].Info != Empty && 6 H->TheCells[cur].value!= key) 7 { 8 cur+= (++CollisionNum<<1) - 1; 9 if (cur>=H->TableSize) 10 cur-=H->TableSize; 11 } 12 return cur; 13 }
第8行到第10行是进行平方探测的快速方法,因为在实现的时候不太好判断进行到第几次探测了,所以直接算i^2不容易,另设个变量监测倒也可以,不过那样挺麻烦的,还占用空间,还多了一次监测变量的++,还多了一次判断,还多了一次平方运算,尤其是算平方开销太大了。所有的这些都会让效率变低。所以我们要把平方计算转化为单纯的+-计算,用i2 - ( i - 1 )2算出他们之间的差距是2 * i - 1,所以F(i)=F( i - 1 ) + 2 * i - 1这个几乎全是加减,乘法用移位代替速度就快多了。如果新的定位越过数组,那么可以通过-Size把它拉回到数组的范围里。这比通常办法快多了,因为他避免了看似要做的乘法和平方。第行的判断顺序很重要,别翻过来,不然短路性质就用不上了。
然后说插入,如果Key存在,就什么也不做,否则就把插入元素放在Find的位置。
void Insert(int key, HashTable H){ Position P=Find(key, H); if (H->TheCells[P].Info != Legitimate) { H->TheCells[P].Info=Legitimate; H->TheCells[P].value=key; } }
虽然平方探测法排除了一次聚集,但是散列到同一位置上的元素将探测相同的备选单元,这么说有点抽象,就是探测的时候都会踩同样的坑,比如说89,49,69这三个数往散列表里放,h0(49)撞到89了,试试i=1,可以了。69撞到89了然后试试i=1,算完之后h1(69)=0和h1(49)又撞了,这就叫“探测到相同的备选单元”,再试一次69才被安置。想想规模更大的表,相撞次数会更多,用f(i)=i2探测的时候分批扎堆,这就叫二次聚集,和之前相比,不是0,1,2,3这样连着一整块扎堆,而是在i=1,4,9,16附近扎堆。这是这两种聚集的区别。
二次聚集是理论上的一个缺憾,下一篇里我们继续讨论如何排除这个缺憾,从而对散列表冲突问题的排解更为高效和优美。不过这需要花费另外一些时间去做乘除法,比平方探测单纯的加减法慢一些,有利有弊吧,实际场景里因地制宜地选择不同模型就好。



