球面模型分解及仿flash标签云
因为还是有一些同学比较感兴趣,所以这里稍作一点分解。既然我们不能参悟高深的数学,那就让我们以娱乐的心态去编码,去学习。
上一篇随笔的评论里我看有童鞋在问具体用了什么数学公式。其实基本上核心的就用了一个数学公式,即球坐标相关的东西。具体可以参考百度百科或者维基百科的球坐标相关释义。我自己恐怕是讲不清楚,所以这里暂就附上《维基百科》上关于球坐标系的解析吧:
球坐标系
在数学里,球坐标系(Spherical coordinate system)是一种三维正交坐标系,专门用球坐标 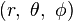 来表示一个点 p 在三维空间的位置(参考图右):原点与点 P 之间的径向距离
来表示一个点 p 在三维空间的位置(参考图右):原点与点 P 之间的径向距离  ,原点到点 P 的连线与正 z-轴之间的天顶角
,原点到点 P 的连线与正 z-轴之间的天顶角 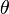 ,以及原点到点 P 的连线,在 xy-平面的投影线,与正 x-轴之间的方位角
,以及原点到点 P 的连线,在 xy-平面的投影线,与正 x-轴之间的方位角 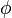 。
。
[编辑]标记
在学术界内,关于球坐标系的标记有好几个不同的约定。按照国际标准化组织建立的约定 (ISO 31-11) ,径向距离、天顶角、方位角,分别标记为 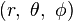 。这种标记在世界各地有许多使用者。通常,物理界的学者也采用这种标记。而在数学界,天顶角与方位角的标记正好相反:
。这种标记在世界各地有许多使用者。通常,物理界的学者也采用这种标记。而在数学界,天顶角与方位角的标记正好相反: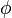 被用来代表天顶角;
被用来代表天顶角;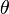 被用来代表方位角。数学界的球坐标标记是
被用来代表方位角。数学界的球坐标标记是  。这种标记的优点是较广的相容性;在二维极坐标系与三维圆柱坐标系里,
。这种标记的优点是较广的相容性;在二维极坐标系与三维圆柱坐标系里, 都同样地代表径向距离,
都同样地代表径向距离,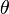 也都同样地代表方位角。本页面采用的是物理标记约定。
也都同样地代表方位角。本页面采用的是物理标记约定。
[编辑]定义
假设 P 点在三维空间的位置的三个坐标是 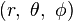 。那么, 0 ≤ r 是从原点到 P 点的距离, 0 ≤ θ ≤ π 是从原点到 P 点的连线与正 z-轴的夹角, 0 ≤ φ < 2π 是从原点到 P 点的连线在 xy-平面的投影线,与正 x-轴的夹角。
。那么, 0 ≤ r 是从原点到 P 点的距离, 0 ≤ θ ≤ π 是从原点到 P 点的连线与正 z-轴的夹角, 0 ≤ φ < 2π 是从原点到 P 点的连线在 xy-平面的投影线,与正 x-轴的夹角。
这里,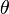 代表天顶角,
代表天顶角,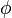 代表方位角。 当
代表方位角。 当 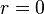 时,
时,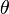 与
与 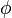 都一起失去意义。当
都一起失去意义。当 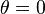 或
或  时,
时,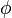 失去意义。
失去意义。
如想要用球坐标,找出点 P 在空间的地点,可按照以下步骤:
- 从原点往正 z-轴移动
 单位,
单位, - 用右手定则,大拇指往 y-轴指,x-轴与 z-轴朝其他手指的指向旋转
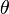 角值,
角值, - 用右手定则,大拇指往 z-轴指,x-轴与 y-轴朝其他手指的指向旋转
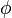 角值。
角值。
[编辑]坐标系变换
三维空间里,有各种各样的坐标系。球坐标系只是其中一种。球坐标系与其他坐标系的变换需要用到特别的方程式。
[编辑]直角坐标系
-
更多资料:直角坐标系
用以下方程式,可以从直角坐标得到球坐标:
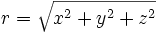 ,
,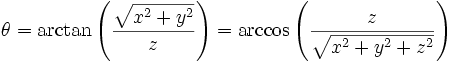 ,
,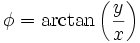 。
。
反过来,可以从球坐标得到直角坐标:
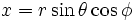 ,
,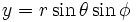 ,
, 。
。
如果大家觉得自己以前学的高数已经完全还给老师了,基本看不懂上面的东西,也不愿意看的话,没关系,我们要用的只是最下面那个球坐标系下的三个公式而已。(其实我自己也基本上都还给老师了...)。
有了公式相信接下来的工作对大多数同仁来说就是小菜一碟了。是的。 仅仅利用上面的三个公式来绘制2d的球面是非常简单的。x和y坐标分别对应我们构成球面的点源的left和top位置,z坐标担负着视井深度的重则,可惜偏偏在DOM的style里面找不到一个好的样式属性来表现它,唯一一个和层级相关的样式就只有z-index了,我们也只好将就点了。那么,公式有了,对应的样式也对应好了,一切就顺理成章了。
我们基于像素模拟的方式,思路大概是,可以自定义我们用来模拟球面的点源的个数,比如200个,随机分布。然后针对每一个元素,分别计算它的三个球坐标,最后和他的样式left,top,和z-index一一对应起来就好。
把上面的公式翻译成js代码:(照搬下来)
a = Math.random()*Math.PI*2,
b = Math.random()*Math.PI*2;
o.x = Math.sin(a)*Math.cos(b)*r;
o.y = Math.sin(a)*Math.sin(b)*r;
o.z = Math.cos(b)*r;
然后进行坐标与dom样式的对应:
_x = o.x*scale,
_y = o.y*scale,
c = Math.round(256+o.z*256);
var sty = o.o.style;
sty.left = Math.round(_x+screen.offsetWidth/2) + 'px';
sty.top = Math.round(_y+screen.offsetHeight/2) + 'px';
sty.width = Math.round(scale*4) + 'px';
sty.height = Math.round(scale*4) + 'px';
sty.background = 'rgb('.concat((c),',',(c),',',(512 - c),')');
sty.zIndex = 500 + Math.round(o.z);
好了,基本就这样,静态的球面大概就出来了:(注意,此时看起来仅仅是二维平面上随机分布的点)
<!--运行没效果的童鞋请刷新一下或者拷贝代码本地运行 -->
不过如果就这个样子的话,的确可以说是一无是处,不仅视觉上根本没有所谓的三维效果,平面上乱七八糟一堆点,没有任何出奇的地方。所以,重要的地方不在于建立静态的球面,而在于怎么让这个静态球面滚动起来,通过滚动的方式给我们视觉上带来误差,这样才会出现三维的效果...
在这种情况下,比较适合的触发方式应该就是鼠标移动,也就是mousemove,这样,我们还能根据鼠标在浏览器可见区的坐标位置去定量的去计算球面每个像素点的移动。最简单的方式:
x : 0,
y : 0
}
document.onmousemove = function(e) {
e = e || window.event;
mouse.x = e.clientX;
mouse.y = e.clientY;
return false;
}
然后可以根据每次得到的鼠标坐标与上一次的鼠标坐标相减得到差值,也就是我们基本的变化量,基于两个方向的(纵向和横向)。然后下一步就要考虑怎么把这两个方向的变化量和刚才建立的球坐标系的三个坐标联系起来。这就涉及到一点点矩阵变换的知识。 当然,要说起来,我自己肯定也是说不清楚,再次贴上维基百科的关于矩阵变换的东西。
二维空间
在二维空间中,旋转可以用一个单一的角 θ 定义。作为约定,正角表示逆时针旋转。把笛卡尔坐标的列向量关于原点逆时针旋转 θ 的矩阵是:
[编辑]三维空间
在三维空间中,旋转矩阵有一个等于单位一的实特征值。旋转矩阵指定关于对应的特征向量的旋转(欧拉旋转定理)。如果旋转角是 θ,则旋转矩阵的另外两个(复数)特征值是 exp(iθ) 和 exp(-iθ)。从而得出 3 维旋转的迹数等于 1 + 2 cos(θ),这可用来快速的计算任何 3 维旋转的旋转角。
3 维旋转矩阵的生成元是三维斜对称矩阵。因为只需要三个实数来指定 3 维斜对称矩阵,得出只用三个是实数就可以指定一个 3 维旋转矩阵。
[编辑]Roll, Pitch 和 Yaw
-
主条目:Tait-Bryan角
生成旋转矩阵的一种简单方式是把它作为三个基本旋转的序列复合。关于右手笛卡尔坐标系的 x-, y- 和 z-轴的旋转分别叫做 roll, pitch 和 yaw 旋转。因为这些旋转被表达为关于一个轴的旋转,它们的生成元很容易表达。
- 绕 x-轴的主动旋转定义为:
 这里的 θx 是 roll 角。
这里的 θx 是 roll 角。
- 绕 y-轴的主动旋转定义为:
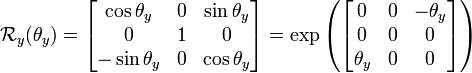 这里的 θy 是 pitch 角。
这里的 θy 是 pitch 角。
- 绕 z-轴的主动旋转定义为:
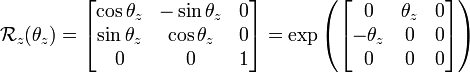 这里的 θz 是 yaw 角。
这里的 θz 是 yaw 角。
上面的东西我看起来也头晕,大部分童鞋可以略过!!
还是直接给出我们所需的绕原点的旋转矩阵吧(由于矩阵不好编辑出来,我就直接写运算后的坐标对应结果):代码表示:
Sphere.x = mouse.x;
var sx = Sphere.y - Sphere.ax;//sx表示每次鼠标位置x向的变化量
var sy = Sphere.x - Sphere.ay; // sy表示鼠标位置y向变化量
Sphere.ax += sx;
Sphere.ay += sy;
/* ==== 把变化量做圆周分解 ==== */
Sphere.cx = Math.cos( sx );
Sphere.sx = Math.sin( sx );
Sphere.cy = Math.cos(-sy );
Sphere.sy = Math.sin(-sy );
然后通过绕原点的矩阵变换公式(这个公式网上可以查到),可以得到我们所需的球坐标和这两个变化量之间的对应关系:这个结果由Gerard Ferrandez提供:
this.y = this.y * Sphere.cx + this.z * -Sphere.sx;
this.z = this.x * -Sphere.sy + z * Sphere.cy;
this.x = this.x * Sphere.cy + z * Sphere.sy;
结合之前的静态球面的三个球坐标,基本上就能得到下面的结果:(随机分布200个点,Gerard Ferrandez的改进版)
基本上,我理解到的原理大致如此,但是可能水平有限,难以讲的透彻,各位包涵。
最后,考虑到我们费那么大劲做这个东西的实用性,苦思冥想,好像只有用在云标签的展示上,于是,大概做了一个仿Flash的云标签展示,当然,无论效率还是平滑度都不能和flash相比,仅作参考,毕竟在运算量不是特别大的时候或许稍微有那么一点可用性:
【仿Flash 球形标签云图】(在20个左右标签时候分布较为均匀)


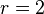 。蓝色圆锥面的
。蓝色圆锥面的 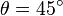 。黄色半平面的
。黄色半平面的 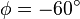 (黄色半平面与 xz-半平面之间的
(黄色半平面与 xz-半平面之间的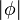 )。 z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个坐标曲面相交于点 P (以黑色的圆球表示)。
)。 z-轴是垂直的,以白色表示。 x-轴以绿色表示。三个坐标曲面相交于点 P (以黑色的圆球表示)。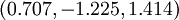 。
。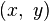 所处的
所处的




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 记一次.NET内存居高不下排查解决与启示
· 探究高空视频全景AR技术的实现原理
· 理解Rust引用及其生命周期标识(上)
· 阿里最新开源QwQ-32B,效果媲美deepseek-r1满血版,部署成本又又又降低了!
· 单线程的Redis速度为什么快?
· 展开说说关于C#中ORM框架的用法!
· SQL Server 2025 AI相关能力初探
· Pantheons:用 TypeScript 打造主流大模型对话的一站式集成库