数据链路层的检错与纠错

通讯链路都不是完全理想的。比特在传输过程中可能会产生比特差错，即1可能变成0，0也可能变成1

1帧包含m个数据位(即报文)和r个冗余位(即校验位)。假设帧的总长度为n，则有 n = m + r。
包含数据和校验位的n位单元，通常称为n位码字

奇偶校验

$\mathrm{奇}\mathrm{偶}\mathrm{校}\mathrm{验}\mathrm{只}\mathrm{能}\mathrm{检}\mathrm{测}\mathrm{出}\mathrm{错}\mathrm{误}，\mathrm{而}\mathrm{无}\mathrm{法}\mathrm{确}\mathrm{定}\mathrm{错}\mathrm{误}\mathrm{数}\mathrm{据}\mathrm{位}\mathrm{具}\mathrm{体}\mathrm{是}\mathrm{哪}\mathrm{一}\mathrm{位}，\mathrm{因}\mathrm{此}\mathrm{无}\mathrm{法}\mathrm{纠}\mathrm{错}$
校验依据：判断传输的一组二进制数据中"1"的个数是奇数还是偶数
奇校验：如果以二进制数据中的"1"的个数是奇数为依据，则是奇校验
偶校验：如果以二进制数据中的"1"的个数是偶数为依据，则是偶校验
$\mathrm{说}\mathrm{明}：\mathrm{采}\mathrm{用}\mathrm{何}\mathrm{种}\mathrm{校}\mathrm{验}\mathrm{必}\mathrm{须}\mathrm{事}\mathrm{先}\mathrm{规}\mathrm{定}\mathrm{好}，\mathrm{通}\mathrm{常}\mathrm{传}\mathrm{输}\mathrm{的}\mathrm{数}\mathrm{据}\mathrm{会}\mathrm{专}\mathrm{门}\mathrm{设}\mathrm{置}\mathrm{一}\mathrm{个}\mathrm{奇}\mathrm{偶}\mathrm{校}\mathrm{验}\mathrm{位}，\mathrm{用}\mathrm{它}\mathrm{来}\mathrm{确}\mathrm{保}\mathrm{发}\mathrm{送}\mathrm{出}\mathrm{去}\mathrm{的}\mathrm{二}\mathrm{进}\mathrm{制}\mathrm{数}\mathrm{据}\mathrm{中}\mathrm{的}"1"\mathrm{的}\mathrm{个}\mathrm{数}\mathrm{为}\mathrm{奇}\mathrm{数}\mathrm{或}\mathrm{偶}\mathrm{数}。$

例如：发送一组8位二进制数，假定第一位为奇偶校验位，后7位为数据位，采用奇校验
1、当发送数据是b'0000111时，发送数据中的"1"有3个，为奇数。此时校验码就为"0"，实际发出的数据为b'00000111;
2、当发送数据时b'0001100时，发送数据中的"1"有2个，为偶数。此时校验码就为"1"，实际发出的数据为b'10001100

海明码

海明码是一种多重奇偶检错系统，它具有检错和纠错功能。海明码中的全部传输码字是由原来的信息和附加奇偶校验位组成的。每一个这种奇偶校验位和信息为被编在传输码字的特定位置上。这种系统组合能找出错误出现的位置，无论是原有信息位还是附加校验位

海明距离：两个码字中不相同的二进制位的个数
两个码字的码距：一个编码系统中任意两个合法编码(码字)之间不同的二进制数位数
编码系统的码距：整个编码系统中任意两个码字的码距的最小值
误码率：传输错误的比特占所传输比特总数的比率

海明码的编码方式

比如：假设需要传输的数据码是"1100"
1、根据公式：计算k = 3,即需要3个校验位

$$2^k>=m+k+1$$

m为信息位，k为校验位
2、校验位按照2^i，即2的次幂，如，1，2，4，8，16，32...留出来，一会填检验码

H7	H6	H5	H4	H3	H2	H1
1	1	0		0

3、需要确认H1、H2、H4这三个校验位都来校验那些2位置
4、将1、2、4的二进制码写出来，最高位补到3位，前面算的k = 3

1	2	4
001	010	100

5、将0替换为*，作为通配符表，如下

1	2	4
**1	*1*	1**

5、将1-7的二进制列出来

1	2	3	4	5	6	7
001	010	011	100	101	110	111

6、将这几个数与上面的通配符表进行匹配(把有与通配表1相同位置的数放一列)

1	2	4
**1	*1*	1**
001(1)	010(2)	100(4)
011(3)	011(3)	101(5)
101(5)	110(6)	110(6)
111(7)	111(7)	111(7)

7、因此我们可以确定：
H1负责H1、H3、H5、H7的校验
H2负责H2、H3、H6、H7的校验
H3负责H4、H5、H6、H7的校验

H7	H6	H5	H4	H3	H2	H1
1	1	0		0

7、用偶校验法，求出校验位是"1"还是"0"
H3、H5、H7的"1"的个数为奇数，因此H1=1
H3、H6、H7的"1"的个数为偶数，因此H2=0
H5、H6、H7的"1"的个数为偶数，因此H3=0
8、至此我们得出了完整的海明码

H7	H6	H5	H4	H3	H2	H1
1	1	0	$0$	0	$0$	$1$

9、查错(|表示按位异或)
第一组p1 = H1 | H3 | H5 | H7
第二组p2 = H2 | H3 | H6 | H7
第三组P3 = H4 | H5 | H6 | H7
10、画图

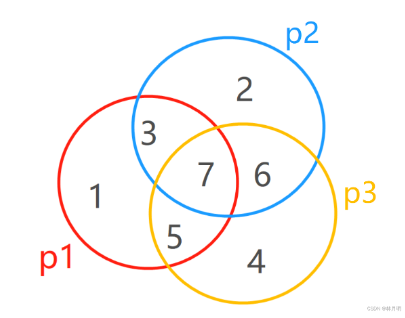
1）如果编码完全正确，那么p1、p2、p3的结果都是0
2）如果p1=1,p2=0,p3=0，则说明p2和p3组的成员2、3、4、5、6、7都没出错，则H1错误
3）以此类推

CRC编码

CRC编码，是指循环冗余码校验，它是利用除法及余数的原理来作错误侦测（Error Detecting）的。

它是利用除法及余数的原理来作错误侦测（Error Detecting）的。实际应用时，发送装置计算出CRC值并随数据一同发送给接收装置，接收装置对收到的数据重新计算CRC并与收到的CRC相比较，若两个CRC值不同，则说明数据通讯出现错误。

生成CRC校验码

例如：假设原始信息串为"10110"，CRC的生成多项式为

$$G(x)=x^4+x+1$$

求CRC校验码
1、因多项式最高次幂为4，所以CRC校验码为4位
2、在原始信息后"添0",即：10110$0000$
3、计算生成多项式

$$G(x)=x^4+x+1=1\ast x^4+0\ast X^3+0\ast x^2+1\ast x^1+1\ast x^0=10011$$

4、使用生成多项式除。利用模2除法。

得到余数"1111"。
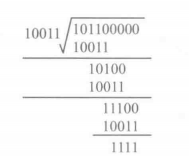
$\mathrm{注}\mathrm{意}：\mathrm{余}\mathrm{数}\mathrm{如}\mathrm{果}\mathrm{不}\mathrm{足}4\mathrm{位}，\mathrm{则}\mathrm{余}\mathrm{数}\mathrm{左}\mathrm{边}\mathrm{用}\mathrm{若}\mathrm{干}\mathrm{个}0\mathrm{补}\mathrm{齐}。\mathrm{如}\mathrm{求}\mathrm{得}\mathrm{余}\mathrm{数}\mathrm{位}"11"，\mathrm{检}\mathrm{验}\mathrm{位}\mathrm{为}"4"，\mathrm{则}\mathrm{补}2\mathrm{个}0\mathrm{得}\mathrm{到}"0011"$
5、将余数添加到原始信息后
上例中，原始信息为"10110",添加余数"1111"后，结果为"101101111"

CRC校验

CRC校验过程与生成过程类似，接收方收了带校验码和的帧后，用多项式G(x)来除。余数为0，则表示信息无错；否则要求发送方进行重传