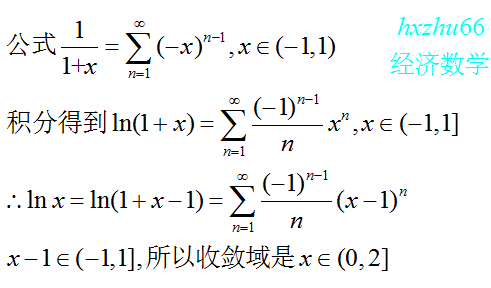lnx展开为幂级数

将函数f(x)=lnx展开成x-1的幂级数

可以简单推导一下：
1/(1-x) = 1+x+x^2+...+x^n+...

integral from 0 to x,

ln(1-x) = x+x^2/2+...+x^n/n+...
lnx = ln(1-(1-x)) = (1-x)+(1-x)^2/2 + ... + (1-x)^n/n + ...
Answer: lnx = -(x-1)+(x-1)^2/2 + ...+ (-1)^n(x-1)^n/n+..., n from 1 to infinity