分布式系统理论基础,以及选举,多数派,租约
ACID:
事务是由一系列对系统中数据进行访问与更新的操作所组成的一个程序执行单元,狭义上的事务特指数据库事务。
一方面,当多个应用程序并发访问数据库时,事务可以在这些应用程序之间提供一个隔离方法,以防止彼此的操作相互干扰,另一方面,事务为数据库操作序列提供了一个从失败中恢复到正常状态的方法,同时提供了数据库即使在宜昌状态下仍能保持数据一致性的方法。 事务具有原子性(Atomicity)、一致性(Consistency)、隔离性(Isolation)、持久性(Durability),简称ACID。
1.原子性,指事务必须是一个原子的操作序列单元,事务中包含的各项操作在一次执行过程中,只允许出现以下两种状态之一,全部成功执行,全部不执行。任何一项操作失败都将导致整个事务失败,同时其他已经被执行的操作都将被撤销并回滚,只有所有操作全部成功,整个事务才算是成功完成。
2.一致性,指事务的执行不能破坏数据库数据的完整性和一致性,一个事务在执行之前和执行之后,数据库都必须处于一致性状态,即事务执行的结果必须是使数据库从一个一致性状态转变到另一个一致性状态,因此当数据库只包含成功事务提交的结果时,就能说数据库处于一致性状态,而如果数据库系统在运行过程中发生故障,有些事务尚未完成就被迫中断,这些未完成的事务对数据库所做的修改有一部分已写入物理数据库,这时数据库就处于一种不正确的状态,或者说是不一致的状态。
3.隔离性,指在并发环境中,并发的事务是相互隔离的,一个事务的执行不能被其他事务干扰,即不同的事务并发操作相同的数据时,每个事务都有各自完整的数据空间,即一个事务内部的操作及使用的数据对其他并发事务是隔离的,并发执行的各个事务之间不能相互干扰。
4.持久性,指一个事务一旦提交,他对数据库中对应数据的状态变更就应该是永久的,即一旦某个事务成功结束,那么它对数据库所做的更新就必须被永久的保存下来,即使发生系统崩溃或者宕机故障,只要数据库能够重新启动,那么一定能够将其恢复到事务成功结束时的状态。
分布式事务
分布式事务是指事务的参与者、支持事务的服务器、资源服务器以及事务管理器分别位于分布式系统的不同节点上,通常一个分布式事务中会涉及对多个数据源或业务系统的操作。 一个分布式事务可以看做是由多个分布式的操作序列组成,通常可以把这一系列分布式的操作序列称为子事务。由于在分布式事务中,各个子事务的执行是分布式的,因此要实现一种能够保证ACID特性的分布式事务处理系统就显得格外复杂。
CAP理论:
CAP定理,指的是在一个分布式系统中,Consistency(一致性)、 Availability(可用性)、Partition tolerance(分区容错性),三者不可得兼!
- 数据一致性(consistency):如果系统对一个写操作返回成功,那么之后的读请求都必须读到这个新数据;如果返回失败,那么所有读操作都不能读到这个数据,对调用者而言数据具有强一致性(strong consistency) (又叫原子性 atomic、线性一致性 linearizable consistency)
- 服务可用性(availability):在集群中一个节点出现故障,集群整体是否还能响应客户端的读写请求。(对数据更新具备高可用)
- 分区容错性(partition-tolerance):在网络分区的情况下,被分隔的节点仍能正常对外服务
在某时刻如果满足AP,分隔的节点同时对外服务但不能相互通信,将导致状态不一致,即不能满足C;
如果满足CP,网络分区的情况下为达成C,请求只能一直等待,即不满足A;
如果要满足CA,在一定时间内要达到节点状态一致,要求不能出现网络分区,则不能满足P。
=======
CAP定理证明中的一致性指强一致性,强一致性要求多节点组成的被调要能像单节点一样运作、操作具备原子性,数据在时间、时序上都有要求。如果放宽这些要求,还有其他一致性类型:
- 序列一致性(sequential consistency):不要求时序一致,A操作先于B操作,在B操作后如果所有调用端读操作得到A操作的结果,满足序列一致性
- 最终一致性(eventual consistency):放宽对时间的要求,在被调完成操作响应后的某个时间点,被调多个节点的数据最终达成一致
可用性在CAP定理里指所有读写操作必须要能终止,实际应用中从主调、被调两个不同的视角,可用性具有不同的含义。当P(网络分区)出现时,主调可以只支持读操作,通过牺牲部分可用性达成数据一致。
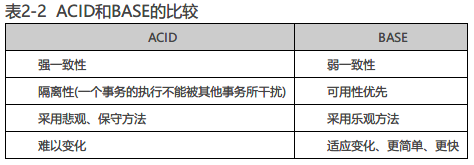
BASE理论:
接受最终一致性的理论支撑是BASE模型,BASE全称是BasicallyAvailable(基本可用), Soft-state(软状态/柔性事务), Eventually Consistent(最终一致性)。
BASE模型在理论逻辑上是相反于ACID模型的概念,它牺牲高一致性,获得可用性和分区容忍性。
最终一致性(Eventually Consistent)。最终一致性是指:经过一段时间以后,更新的数据会到达系统中的所有相关节点。这段时间就被称之为最终一致性的时间窗口
选举:
选举(election)是分布式系统实践中常见的问题,通过打破节点间的对等关系,选得的leader(或叫master、coordinator)有助于实现事务原子性、提升决议效率。
多数派(quorum)的思路帮助我们在网络分化的情况下达成决议一致性,在leader选举的场景下帮助我们选出唯一leader。租约(lease)在一定期限内给予节点特定权利,也可以用于实现leader选举。
一致性问题(consistency)是独立的节点间如何达成决议的问题,选出大家都认可的leader本质上也是一致性问题,因而如何应对宕机恢复、网络分化等在leader选举中也需要考量。
Bully算法[1]是最常见的选举算法,其要求每个节点对应一个序号,序号最高的节点为leader。leader宕机后次高序号的节点被重选为leader,过程如下:
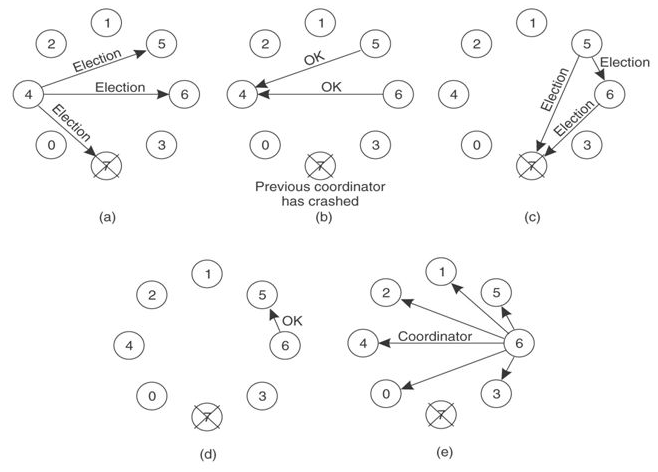
(a). 节点4发现leader不可达,向序号比自己高的节点发起重新选举,重新选举消息中带上自己的序号
(b)(c). 节点5、6接收到重选信息后进行序号比较,发现自身的序号更大,向节点4返回OK消息并各自向更高序号节点发起重新选举
(d). 节点5收到节点6的OK消息,而节点6经过超时时间后收不到更高序号节点的OK消息,则认为自己是leader
(e). 节点6把自己成为leader的信息广播到所有节点
多数派:
在网络分化的场景下以上Bully算法会遇到一个问题,被分隔的节点都认为自己具有最大的序号、将产生多个leader,这时候就需要引入多数派(quorum)。多数派的思路在分布式系统中很常见,其确保网络分化情况下决议唯一。
多数派的原理说起来很简单,假如节点总数为2f+1,则一项决议得到多于 f 节点赞成则获得通过。leader选举中,网络分化场景下只有具备多数派节点的部分才可能选出leader,这避免了多leader的产生。
多数派的思路还被应用于副本(replica)管理,根据业务实际读写比例调整写副本数Vw、读副本数Vr,用以在可靠性和性能方面取得平衡。
租约:
选举中很重要的一个问题,以上尚未提到:怎么判断leader不可用、什么时候应该发起重新选举?最先可能想到会通过心跳(heart beat)判别leader状态是否正常,但在网络拥塞或瞬断的情况下,这容易导致出现双主。
租约(lease)是解决该问题的常用方法,其最初提出时用于解决分布式缓存一致性问题,后面在分布式锁等很多方面都有应用。
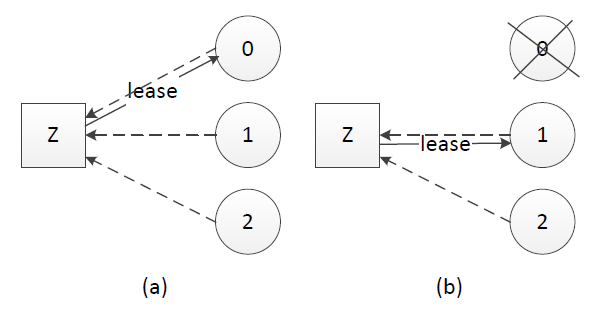
租约的原理同样不复杂,中心思想是每次租约时长内只有一个节点获得租约、到期后必须重新颁发租约。假设我们有租约颁发节点Z,节点0、1和2竞选leader,租约过程如下:
(a). 节点0、1、2在Z上注册自己,Z根据一定的规则(例如先到先得)颁发租约给节点,该租约同时对应一个有效时长;这里假设节点0获得租约、成为leader
(b). leader宕机时,只有租约到期(timeout)后才重新发起选举,这里节点1获得租约、成为leader
租约机制确保了一个时刻最多只有一个leader,避免只使用心跳机制产生双主的问题。在实践应用中,zookeeper、ectd可用于租约颁发。
http://blog.csdn.net/dellme99/article/details/15340955
https://draveness.me/consensus
http://www.cnblogs.com/bangerlee/p/5328888.html
http://blog.csdn.net/chen77716/article/details/30635543
http://www.cnblogs.com/duanxz/p/5229352.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)
2016-11-07 Java Synchronized的用法