算法的时间复杂度
预习:
先来复习一下中学的课程:
指数函数:
y=函数(a为常数且以a>0,a≠1)叫做指数函数,函数的定义域是 R
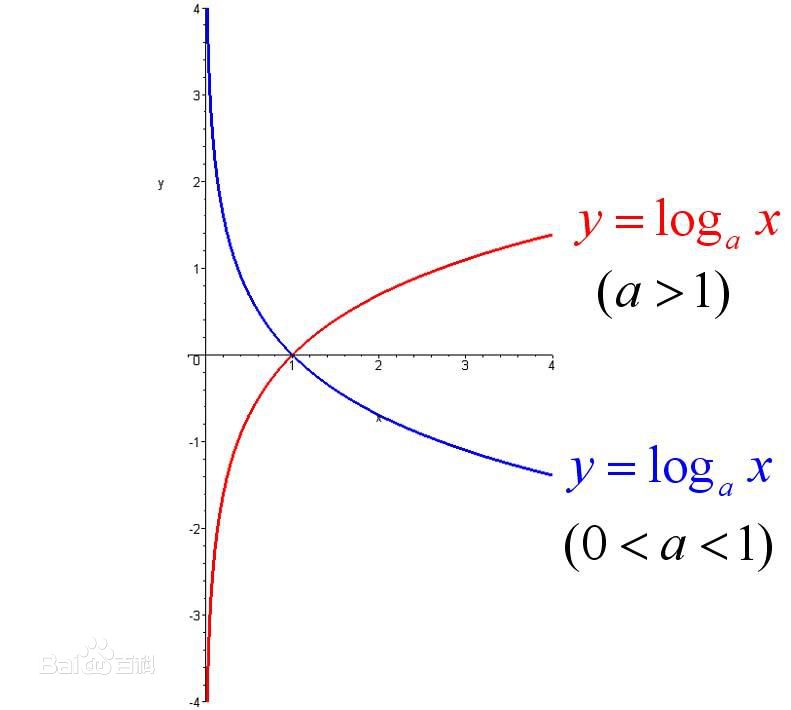
对数函数:
如果(a>0,且a≠1),那么数x叫做以a为底N的对数,记作,读作以a为底N的对数,其中a叫做对数的底数,N叫做真数。
一般地,函数(a>0,且a≠1)叫做对数函数,也就是说以幂(真数)为自变量,指数为因变量,底数为常量的函数,叫对数函数
对数的表示及性质:
-
以a为底N的对数记作:
-
以10为底的常用对数: =
-
以无理数为底的自然对数记作: =
-
零没有对数.
-
在实数范围内,负数无对数。 在虚数范围内,负数是有对数的。
自然数e
数学中的自然数e,讲解地址: http://www.ruanyifeng.com/blog/2011/07/mathematical_constant_e.html
常见时间复杂度
常见的时间复杂度量级有:
- 常数阶O()
- 对数阶O()
- 线性阶O()
- 线性对数阶O()
- 平方阶O()
- 立方阶O()
- K次方阶O()
- 指数阶()
上面从上至下依次的时间复杂度越来越大,执行的效率越来越低。
常数阶O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1),如:
int i = 1;
int j = 2;
++i;
j++;
int m = i + j;
上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
线性阶O(n)
这个在最开始的代码示例中就讲解过了,如:
for(i=1; i<=n; ++i)
{
j = i;
j++;
}
这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
对数阶O(logN)
还是先来看代码:
int i = 1;
while(i<n)
{
i = i * 2;
}
从上面代码可以看到,在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。我们试着求解一下,假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x =
也就是说当循环 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(logN)
线性对数阶O(nlogN)
线性对数阶O() 其实非常容易理解,将时间复杂度为O()的代码循环N遍的话,那么它的时间复杂度就是 n * O()
就拿上面的代码加一点修改来举例:
for(m=1; m<n; m++)
{
i = 1;
while(i<n)
{
i = i * 2;
}
}
平方阶O(n²)
平方阶O(n²) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²) 了。
举例:
for(x=1; i<=n; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(),即 O()
如果将其中一层循环的n改成m,即:
for(x=1; i<=m; x++)
{
for(i=1; i<=n; i++)
{
j = i;
j++;
}
}
那它的时间复杂度就变成了 O()
立方阶O(n³)、K次方阶O(n^k)
参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似。
取最大复杂度作为整个算法的复杂度
public static void print1(int n){
for (int i=0;i<1000;i++){
System.out.println(i);
}
for (int j=0;j<n;j++){
System.out.println(j);
}
for (int p=0;p<n;p++){
for (int q=0;q<n;q++){
System.out.println(p+q);
}
}
}
这个例子中有三个循环,首先第一个,是一个常量,那么根据前面的结论,不论这个常量是多大,都属于常量级,所以第一个循环中的复杂度为 O(1),第二个和第三个循环,复杂度分别为 O(n) 和 O(n²)。
也就是这一段代码中有三段代码产生了三种不同复杂度,而且这三个复杂度可以很明显得到的大小关系为:O(1)<O(n)<O(n²),像这种在同一个算法中有明确大小关系的,我们就可以直接取最大值作为这个算法的复杂度,所以这个例子中算法的复杂度就是 O(n²)。
时间复杂度类型
根据实际情况,又可以将时间复杂度从以下四个方面来进一步分析:
- 最好时间复杂度
- 最坏时间复杂度
- 平均时间复杂度
- 均摊时间复杂度
最好时间复杂度
demo:
public static int findEle(int[] arr,int val){
if (null == arr || arr.length == 0){
return -1;
}
for (int i=0;i<arr.length;i++){
if (arr[i] == val){
return i;
}
}
return -1;
}
这个方法就是在一个指定数组中找到指定元素的下标,找不到就返回 -1,这个方法比较简单,应该比较好理解。
注意这个方法中的循环体,如果找到元素,那么就直接返回,这就会有一个现象,那就是我这个循环体到底会循环多少次是不确定的,可能是 1 次,也可能是 n(假设数组的长度) 次,所以假如我们要找的元素就在数组中的第一个位置,那么我循环一次就找到了,这个算法的最好复杂度就是 O(1)。
最坏时间复杂度
理解了最好时间复杂度,那么最坏时间复杂度也很好理解了,那就是数组中不存在我要找到元素,或者说最后一个值才是我要找的元素,那么这样我就必须循环完整个数组,那么时间复杂度就是 O(n),这也就是最坏时间复杂度。
平均时间复杂度
最好时间复杂度和最坏时间复杂度毕竟只有特殊情况才会发生,概率还是相对较小,所以我们很容易就想到我们也需要有一个平均时间复杂度。
我们简单的来分析一下,为了便于分析,我们假设一个元素在数组和不在数组中的概率都为 1/2,然后假如在数组在,那么又假设元素出现在每个位置的概率也是一样的,也就是每个位置出现元素的概率为: 1/n。
所以最终得到的平均时间复杂度应该等于元素在数组中和元素不在数组中两种情况相加。
- 元素在数组中的复杂度
因为元素在数组中的概率为 ,然后在每个位置出现的概率也为 。假如元素出现在第一个位置,复杂度为 ;假如元素出现在第二个位置,复杂度为 ,最终得到当前场景下时间复杂度为:。
- 元素不在数组中的复杂度
前面已经假定了元素不在数组中的概率为 ,所以当前场景下的时间复杂度为:,因为元素不在数组中,那么这个算法必然会将整个循环执行完毕,也就循环是 n 次。
最后我们把两种情况的复杂度之和相加就得到了平均时间复杂度:,最终我们将常数类的系数忽略掉,就得到了平均时间复杂度为 。
均摊时间复杂度
均摊时间复杂度的算法需要使用摊还分析法,计算方式相对有点复杂,而且使用场景很有限,本文就不做过多介绍了。
空间复杂度
空间复杂度全称就是渐进空间复杂度,用来表示算法的存储空间与数据规模之间的增长关系。和时间复杂度一样,空间复杂度也是用大 O 进行表示。
空间复杂度主要看在一个算法当中到底有没有使用到了额外的空间来进行存储数据,然后判断这个额外空间的大小会不会随着 n 的变化而变化,从而得到空间复杂度。
Demo:
public static void init(int n){
int a = 0;
int arr[] = new int[n];
for (int i=0;i<n;i++){
arr[i]=n;
}
}
一开始定义了一个变量,这里需要空间,但是这是一个常量级的(不随 n 的变化而变化),然后再定义了一个数组,数组的长度为 n,这里数组也需要占用空间,而且数组的空间是随着 n 的变化而变化的,其余代码没有占用额外空间,所以我们就可以认为上面示例中的空间复杂度为 O(n)。
对于算法的空间复杂度也可以简单的进行总结一下:
- 如果申请的是有限个数(常量)的变量,空间复杂度为
O(1)。 - 如果申请的是一维数组,队列或者链表等,那么空间复杂度为
O(n)。 - 如果申请的是二维数组,那么空间复杂度为
O(n²)。 - 如果是在循环体中申请的数组等,可能就需要取嵌套的乘积来作为空间复杂度,这种就需要具体的进一步分析。
总结
常用算法
时间复杂度大小
算法复杂度总常见的表示形式为常数级、对数级、线性级度、平方级、指数级,其运算时间的典型函数增长情况如图所示。
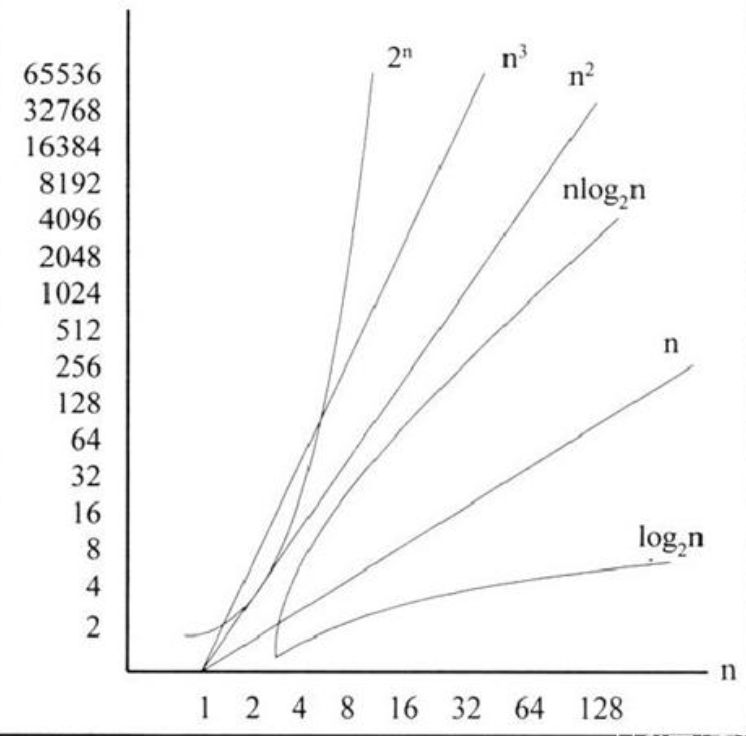
简单来说,当n足够大时,复杂度与时间效率有如下关系(c是一个常量):


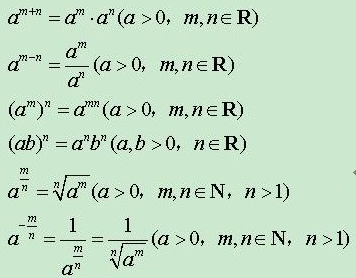



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· AI与.NET技术实操系列(二):开始使用ML.NET
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 【杭电多校比赛记录】2025“钉耙编程”中国大学生算法设计春季联赛(1)
2013-12-12 JavaScript:Array属性方法