python岭迹图绘制函数

一.岭迹图是什么？

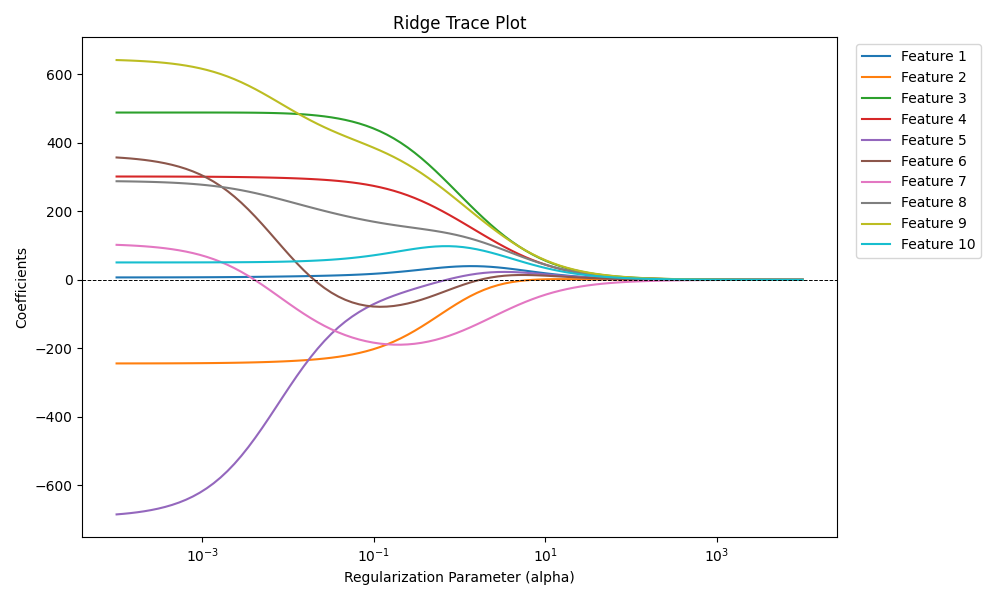
        岭迹图（Ridge Trace Plot）是一种可视化工具，用于展示岭回归中正则化参数（$\alpha$）对回归系数的影响。它能帮助我们理解特征的稳定性和正则化在控制模型复杂度中的作用。

二.什么时候需要看岭迹图？

1. 存在共线性特征时

   • 当特征间高度相关，普通最小二乘法（OLS）回归的系数会变得不稳定。
   • 岭迹图帮助选择合适的正则化强度，缓解共线性问题。

2. 模型复杂度调整时

   • 如果模型过拟合，可以通过岭迹图观察较大的 $\alpha$ 是否能有效控制模型复杂度。
   • 如果模型欠拟合，则观察适中的 $\alpha$ 是否能有效提高拟合能力。

3. 特征选择或降维时

   • 岭迹图可帮助识别对模型贡献较小的特征，便于特征选择或进一步降维。

4. 解释非线性模型时

• 尽管岭迹图主要用于线性模型，但也可以用于理解岭回归对特定问题的建模方式。

三.岭迹图能说明什么问题？

1. 正则化的作用

   • $\alpha$ 控制模型的复杂度：小$\alpha$，模型复杂，可能过拟合；大$\alpha$，模型简单，可能欠拟合。
   • 通过观察岭迹图，可以选择一个合适的 $\alpha$，在模型复杂度和拟合能力之间取得平衡。

2. 特征的稳定性

   • 稳定的特征对预测更有意义，不易受共线性或噪声影响。
   • 变化剧烈的特征可能需要进一步处理，比如移除、归一化或降维。

3. 共线性问题

   • 如果某些系数在 $\alpha$ 较小时变得极大或波动剧烈，可能存在特征共线性问题。

4. 特征重要性

   • 岭迹图可以直观展示哪些特征对预测目标最重要，以及它们的重要性如何随正则化变化。

四.分析岭迹图

1. $\alpha$ 较小时（接近左侧）

   • 正则化强度较低，岭回归趋近于普通最小二乘法（OLS）。
   • 系数可能波动较大，尤其在共线性特征存在时，系数值可能很高甚至不稳定。

2. $\alpha$ 增大时

   • 正则化逐渐加强，各特征的系数被逐渐压缩。
   • 特征间的共线性被削弱，系数值趋于稳定。

3. $\alpha$ 很大时（接近右侧）

   • 强正则化将所有系数压缩接近 0。
   • 模型变得过于简单，可能导致欠拟合。

　特征行为观察

• 稳定性：如果某条曲线随着 $\alpha$ 增大仍保持较大绝对值，说明该特征对目标变量的影响更显著、更稳定。
• 敏感性：某些曲线在 $\alpha$ 较小时变化剧烈，表明这些特征可能高度共线或受噪声影响。

五.输出示例

　　现象1：一条曲线始终接近 0

　　　　该特征对预测目标贡献较小，可能是无关特征。

　　现象2：某些曲线在 $\alpha$ 较小时波动剧烈，但逐渐趋于稳定

　　　　这些特征可能存在共线性，但岭回归缓解了问题。

　　现象3：大部分曲线在 $\alpha$ 增大时趋近 0

　　　　说明正则化削弱了所有特征的重要性，$\alpha$ 太大可能导致欠拟合。

　　通过观察这些现象，可以有效调整模型参数和特征选择，从而构建更稳健的模型。

 

 

留到最后：python岭迹图函数代码

# 绘制岭迹图
def Ridge_Plot(x_train, y_train):
    import numpy as np
    import matplotlib.pyplot as plt
    from sklearn.linear_model import Ridge

    # 确保 y_train 是一维数组
    y_train = np.ravel(y_train)  # 自动将 (n, 1) 转换为 (n,)

    # 定义正则化参数范围
    alphas = np.logspace(-4, 4, 100)

    # 存储系数
    coefs = []

    # 遍历每个正则化参数，训练岭回归模型
    for alpha in alphas:
        ridge = Ridge(alpha=alpha)
        ridge.fit(x_train, y_train)
        coefs.append(ridge.coef_)

    # 转换系数为数组
    coefs = np.array(coefs)

    # 绘制岭迹图
    plt.figure(figsize=(10, 6))
    for i in range(x_train.shape[1]):
        plt.plot(alphas, coefs[:, i], label=f'Feature {i + 1}')
    plt.xscale('log')
    plt.xlabel('Regularization Parameter (alpha)')
    plt.ylabel('Coefficients')
    plt.title('Ridge Trace Plot')
    plt.axhline(0, color='black', linestyle='--', linewidth=0.7)
    plt.legend(loc='upper right', bbox_to_anchor=(1.2, 1), ncol=1)
    plt.tight_layout()
    plt.show()

Ridge_Plot(x_train=X_train,y_train=y_train)

值得注意的是，这里顺便学一个方法：

1.abs() #取绝对值

2.（22，1）类型数据与（22，）类型数据，

 

特性	(22, 1)	(22,)
维度	二维（矩阵）	一维（向量）
适用场景	矩阵运算、机器学习特征输入	数组运算、数据表示
广播行为	明确列方向	没有方向，需要额外处理
相互转换方法	.squeeze() .rabel() .reshape(-1)	.reshape(-1, 1)

选择形状时，要根据上下文需求（是否需要明确区分行列结构）和函数的要求（如线性模型对输入特征形状的要求）来判断使用哪种形式。