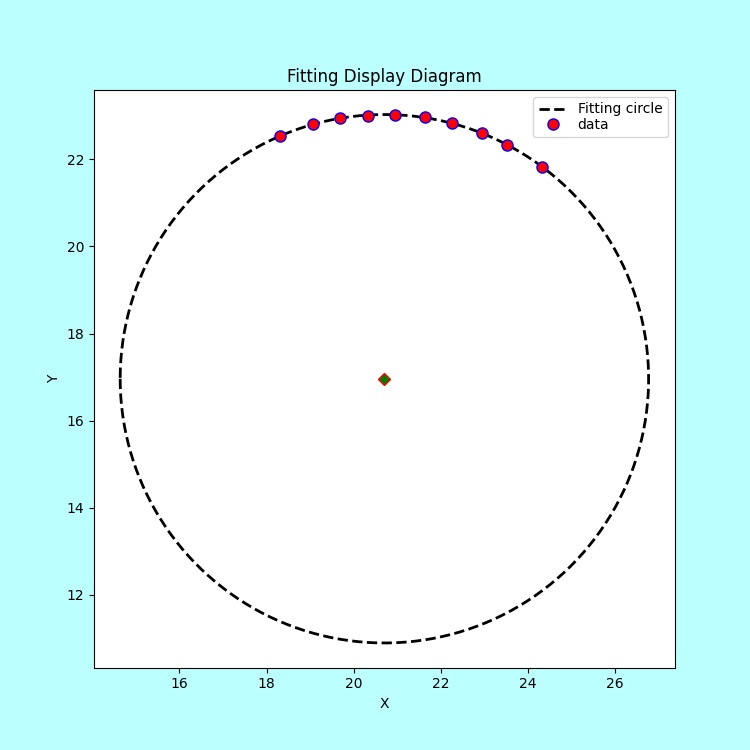
自定义点拟合最合适的圆
写入拟合点:x与y对应
#输入所需拟合的点 x = r_[20.96, 22.25, 23.51, 24.32, 21.64, 22.94,20.32,19.68,19.07,18.31] y = r_[23.02, 22.83, 22.34, 21.83, 22.96, 22.61,23.00,22.94,22.82,22.53]
代码如下:
1 #导入第三方库 2 import functools 3 from numpy import * 4 from scipy import optimize 5 from matplotlib import pyplot as plt, cm, colors 6 7 legendone = "Fitting circle" 8 #输入所需拟合的点 9 x = r_[20.96, 22.25, 23.51, 24.32, 21.64, 22.94,20.32,19.68,19.07,18.31] 10 y = r_[23.02, 22.83, 22.34, 21.83, 22.96, 22.61,23.00,22.94,22.82,22.53] 11 12 # 质心坐标 13 x0 = mean(x) 14 y0 = mean(y) 15 16 #修饰器加以修饰反馈结果 17 def Decorator(s): 18 @functools.wraps(s) 19 def wrapped(*args): 20 wrapped.ncalls +=1 21 return s(*args) 22 wrapped.ncalls = 0 23 return wrapped 24 25 def R_one(xc, yc): 26 return sqrt((x - xc) ** 2 + (y - yc) ** 2) 27 28 @Decorator 29 def f_2(c): 30 Ri = R_one(*c) 31 return Ri - Ri.mean() 32 33 #圆心估计 34 center_estimate = x0, y0 35 center_2, _ = optimize.leastsq(f_2, center_estimate) 36 37 xc_2, yc_2 = center_2 38 Ri_2 = R_one(xc_2, yc_2) 39 #拟合圆的半径 40 R_2 = Ri_2.mean() 41 residu_2 = sum((Ri_2 - R_2)**2) 42 residu2_2 = sum((Ri_2**2-R_2**2)**2) 43 ncalls_2 = f_2.ncalls 44 #输出列表 45 plist = '%-22s %10.5f %10.5f %10.5f %10d %10.6f %10.6f %10.2f' 46 47 #输出图 48 plt.close('all') 49 def Drawing_display(residu2=False): 50 plt.figure(figsize=(7.5, 7.5),facecolor='#BBFFFF',dpi=100) 51 plt.axis('equal') 52 theta_fit = linspace(-pi, pi, 180) 53 54 x_fit2 = xc_2 + R_2 * cos(theta_fit) 55 y_fit2 = yc_2 + R_2 * sin(theta_fit) 56 plt.plot(x_fit2, y_fit2, 'k--', label=legendone, lw=2) 57 58 plt.plot([xc_2], [yc_2], 'gD', mec='r', mew=1) 59 60 # 坐标画图 61 plt.xlabel('X') 62 plt.ylabel('Y') 63 64 # 数据横表 65 plt.plot(x, y, 'ro', label='data', ms=8, mec='b', mew=1) 66 plt.legend(loc='best', labelspacing=0.1) 67 plt.title('Fitting Display Diagram') 68 plt.savefig('拟合展示图%d.jpg' % (2 if residu2 else 1)) 69 Drawing_display(residu2=True) 70 plt.show() 71 72 def main(): 73 print("------------圆的拟合结果------------") 74 print("质心坐标:({:.2f},{:.2f})".format(x0,y0)) #保留两位小数 75 print("圆心:({:.2f},{:.2f})".format(xc_2,yc_2)) #保留两位小数 76 print("半径:{:.2f}".format(R_2)) #保留两位小数 77 print(('\n%-22s' + ' %10s' * 7) % tuple('datas Xc Yc Rc nb_calls std(Ri) residu residu2'.split())) 78 print('-' * (22 + 7 * (10 + 1))) 79 print(plist % (legendone, xc_2, yc_2, R_2, ncalls_2, Ri_2.std(), residu_2, residu2_2)) 80 if __name__ == '__main__': 81 main()
拟合效果图如图: