HDU 5120 Intersection

Intersection

Problem Description

Matt is a big fan of logo design. Recently he falls in love with logo made up by rings. The following figures are some famous examples you may know.


A ring is a 2-D figure bounded by two circles sharing the common center. The radius for these circles are denoted by r and R (r < R). For more details, refer to the gray part in the illustration below.


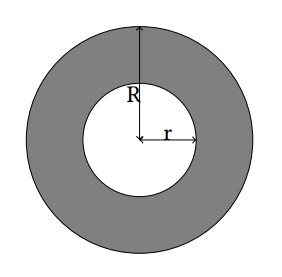
Matt just designed a new logo consisting of two rings with the same size in the 2-D plane. For his interests, Matt would like to know the area of the intersection of these two rings.

 

 

Input

The first line contains only one integer T (T ≤ 10⁵), which indicates the number of test cases. For each test case, the first line contains two integers r, R (0 ≤ r < R ≤ 10).

Each of the following two lines contains two integers x_i, y_i (0 ≤ x_i, y_i ≤ 20) indicating the coordinates of the center of each ring.

 

 

Output

For each test case, output a single line “Case #x: y”, where x is the case number (starting from 1) and y is the area of intersection rounded to 6 decimal places.

 

 

Sample Input

2

2 3

0 0

0 0

2 3

0 0

5 0

 

 

 

Sample Output

Case #1: 15.707963

Case #2: 2.250778

#include<iostream>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef double db;
const db PI=acos(-1.0);
struct point
{
    db x,y;
}p[2];
struct circle
{
    point O;
    db r;
}C[4];
db distcal(point a,point b)
{
    return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
db areacal(circle a,circle b)
{
    if(a.r>b.r)swap(a,b);
    db d=distcal(a.O,b.O);
    if(d==0.0||d+a.r<=b.r){db t=a.r;return PI*t*t;}
    if(a.r+b.r<=d)return 0.0;
    db th1=acos((a.r*a.r+d*d-b.r*b.r)/(2*a.r*d));
    db th2=acos((b.r*b.r+d*d-a.r*a.r)/(2*b.r*d));
    db are1=a.r*a.r*th1;
    db are2=b.r*b.r*th2;
    db are3=a.r*d*sin(th1);
    return are1+are2-are3;
}
int main()
{
    int T;
    scanf("%d",&T);
    for(int kase=1;kase<=T;kase++)
    {
        db r,R;
        scanf("%lf%lf",&r,&R);
        scanf("%lf%lf%lf%lf",&p[0].x,&p[0].y,&p[1].x,&p[1].y);
        C[0].O=p[0],C[0].r=R;
        C[1].O=p[0],C[1].r=r;
        C[2].O=p[1],C[2].r=R;
        C[3].O=p[1],C[3].r=r;
        db ans=areacal(C[0],C[2])+areacal(C[1],C[3])-2.0*areacal(C[0],C[3]);
        printf("Case #%d: %.6f\n",kase,ans);
    }
    return 0;
}
/*
1
1 10
0 0
1 0
*/