数据结构与算法-算法基础二

 

再来看一下二分查找，以及快速排序、堆排序

二分查找

    /**
     * 二分查找，每次只取中位数元素进行比较，这样比较的前提是序列有序
     */
    @org.junit.Test
    public void testBSearch() {

        int left = 0;
        int right = arr.length-1;
        for(;left<=right;) {
            int middle = (left + right)/2;
            if (arr[middle] > toSearch) {
                right = middle-1;
            } else if (arr[middle] < toSearch) {
                left = middle+1;
            }else {
                index = middle;
                break;
            }
        }
    }

 

快速排序

快速排序的基本思想如下：

1. 对数组进行随机化。
2. 从数列中取出一个数作为中轴数(pivot)。
3. 将比这个数大的数放到它的右边，小于或等于它的数放到它的左边。
4. 再对左右区间重复第三步，直到各区间只有一个数。

特点：适合大量、无序的数据，不需要占用额外空间。

改进：

　　在区间较小时，可以转换为插入排序。

示例：

 

    /**
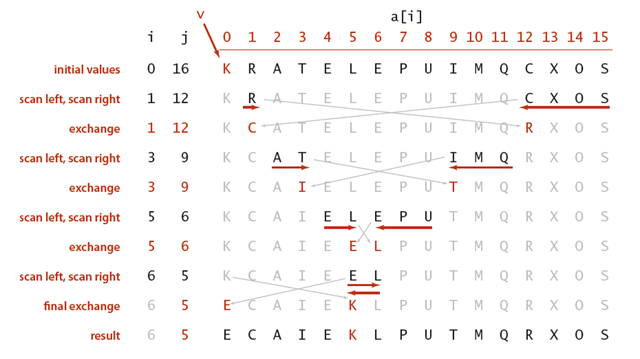
     * 快速排序，每轮排序都会确定一个元素的最终位置，并将其余元素放置在该元素两侧。
     */
    @org.junit.Test
    public void testQuick() {
        quick(arr, 0, arr.length-1);
    }
    private void quick(Integer[] arr, int left, int right) {
        if (left >= right) {
            return;
        }
        int mid = split(arr, left, right);
        quick(arr, left, mid-1);
        quick(arr, mid+1, right);
    }
    private int split(Integer[] arr, int left, int right) {
        int temp = arr[left];
        for(;left<right;) {
            for(;left<right&&arr[right]>=temp;right--) {
            }
            if (left < right) {
                arr[left++] = arr[right];
            }
            for(;left<right&&arr[left]<temp;left++) {
            }
            if (left < right) {
                arr[right--] = arr[left];
            }
        }
        arr[left] = temp;
        return left;
    }

 

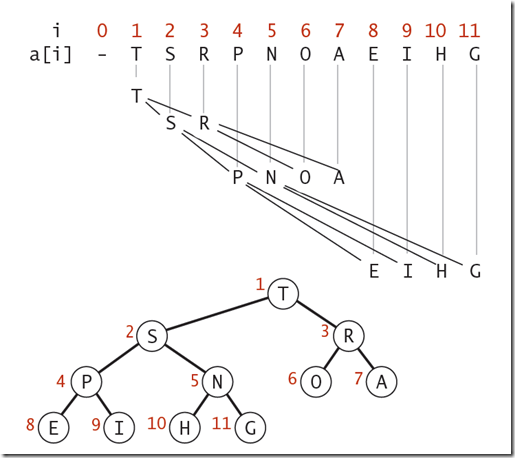
堆排序

大顶堆的定义：有n个元素的序列｛k1, k2, k3, ..., kn｝，满足k_i>=k_2i，k_i>=k_2i+1。

使用场景：优先队列（priority queue）。

大顶堆的构建：

　　插入元素时，需要自下而上筛选出最大元素至树根；

　　删除（树根）元素时，需要自上而下重新构建堆结构（首先要将右下角元素，即第n个元素，移至树根）。

使用数字表示一个大顶堆（形状上是一个完全二叉树）：

 

        for(int i=n/2; i>=1; i--) {//构建大顶堆
            adjust(toSort, i, n);
        }
        for(int i=1; i<n; i++) {//排序
            int t = toSort[n-i+1];
            toSort[n-i+1] = toSort[1];
            toSort[1] = t;
            adjust(toSort, 1, n-i);
        }

    private void adjust(Integer[] arr, int parentIndex, int n) {
        int max = parentIndex;
        int sonIndex;
        for(;parentIndex*2<=n;) {
            if ((sonIndex=parentIndex * 2)<=n&&arr[sonIndex] != null && arr[max] < arr[sonIndex]) {
                max = sonIndex;
            }
            if ((sonIndex=parentIndex * 2+1)<=n&&arr[sonIndex] != null && arr[max] < arr[sonIndex]) {
                max = sonIndex;
            }
            if (max != parentIndex) {
                int t = arr[max];
                arr[max] = arr[parentIndex];
                arr[parentIndex] = t;
                parentIndex = max;
            }else {
                break;
            }
        }
    }