Logistic回归(LogisticRegression,LR)
它名字叫回归,但其实是用来二分类的
1.logistic函数
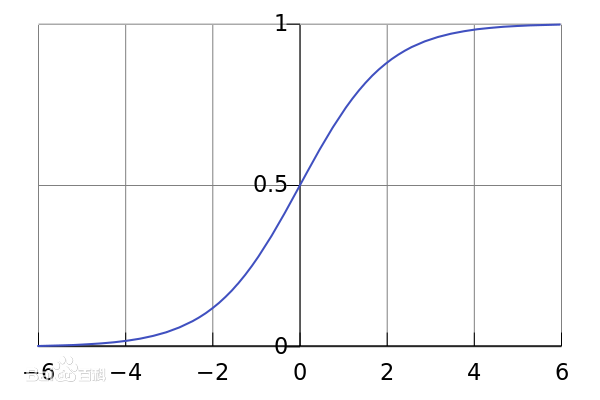
logistic函数 = sigmoid曲线(S型曲线)
标准logistic函数:\(𝜎(x) = \frac{1}{1 + e^{-x}}\)
𝜎′(𝑥)=𝜎(𝑥)(1−𝜎(𝑥)).
2.交叉熵损失函数(Cross-Entropy Loss Function)
3.梯度下降法
\[𝜃_{𝑡+1} = 𝜃_𝑡 − 𝛼\frac{𝜕J(𝜃)}{𝜕𝜃}
\]
其中𝜃𝑡为第𝑡次迭代时的参数值, 𝛼为搜索步长. 在机器学习中, 𝛼一般称为学习率 (LearningRate) .
\(增广特征向量𝒙=[𝑥_1,⋯,𝑥_𝐷,1]^T, 增广权重向量𝒘=[𝑤_1,⋯,𝑤_𝐷,𝑏]^T\)
\[①\quad 𝑝(𝑦=1|𝒙) = 𝜎(𝒘^T𝒙) = \frac{1}{1 + e^{-w^Tx}} = p_𝒘(x) = x是1类的概率 = 𝜎(z)
\]
\[②\quad 某样本x的损失Cost(p(x),y) = \left\{
\begin{aligned}
\begin{cases}
-\log(p) & \text{y=1} \\
-\log(1-p) & \text{y=0}
\end{cases} \qquad(1)
\\
\\y·f(1) + (1-y)·f(0) \qquad(2)
\\
\\y·[-\log(p)] + (1-y)·[-\log(1-p)] \qquad(3)
\end{aligned}\right.\]
\[③\quad 总损失J(𝒘) \left\{
\begin{align*}
& = \frac 1N \sum\limits_{n=1}^N Cost(p(x_i),y_i)\\
& = \frac 1N \sum\limits_{n=1}^N \quad y_i·[-\log(p(x_i))] + (1-y_i)·[-\log(1-p(x_i))]\\
& = -\frac 1N \sum\limits_{n=1}^N \quad y_i·\log(p(x_i)) + (1-y_i)·\log(1-p(x_i))\\
& = -\frac 1N \sum\limits_{n=1}^N \quad y_i·\log(𝜎(z_i)) + (1-y_i)·\log(1-𝜎(z_i))
\end{align*}
\right.
\]
②(1)注: \(Cost(p(x),y) = -\log(p) \qquad ,\text{y=1}\) : p(x)越接近1,即x是1类的概率越大,损失越小
\(\qquad\quad\) \(Cost(p(x),y) = -\log(1-p) \quad ,\text{y=0}\) : p(x)越接近0,即x是1类的概率越小,损失越小
\[\frac{𝜕J(𝒘)}{𝜕𝒘}\left\{
\begin{align*}
& = -\frac 1N \sum\limits_{n=1}^N \quad y_i\frac{𝜎'(z_i)}{𝜎(z_i)} + (y_i-1)\frac{𝜎'(z_i)}{1-𝜎(z_i)}\\
& = -\frac 1N \sum\limits_{n=1}^N \quad y_i\frac{𝜎(z_i)(1−𝜎(z_i))z_i'}{𝜎(z_i)} + (y_i-1)\frac{𝜎(z_i)(1−𝜎(z_i))z_i'}{1-𝜎(z_i)}\\
& = -\frac 1N \sum\limits_{n=1}^N \quad z_i'(y_i-𝜎(z_i))\\
& = -\frac 1N \sum\limits_{n=1}^N \quad (𝒘^T𝒙_i)'(y_i-𝜎(z_i))\\
& = -\frac 1N \sum\limits_{n=1}^N \quad 𝒙_i(y_i-𝜎(z_i))\\
& = -\frac 1N \sum\limits_{n=1}^N \quad 𝒙_i(y_i-p_𝒘(x_i))
\end{align*}
\right.
\]
\[𝒘_{𝑡+1}\left\{
\begin{align*}
& = 𝒘_𝑡 − 𝛼\frac{𝜕J(𝒘)}{𝜕𝒘}\\
& = 𝒘_𝑡 + 𝛼\frac 1N \sum\limits_{n=1}^N 𝒙_i(y_i-p_𝒘(x_i))\ \ ,\ p_𝒘(x_i)是当参数为𝒘𝑡时,Logistic回归模型的输出
\end{align*}
\right.
\]

