模拟退火算法（Simulate Anneal，SA）

求全局最小点。
每次随机出一个新解。如果这个解更优，则采纳它；否则以一定概率采纳它。
设这个新的解与上一个解的差为ΔE，温度为T，k 为一个随机数，离子趋于平衡的概率（即可采纳的概率）为:

\[P_k=e^{-\frac{\Delta E}{kT}} \]

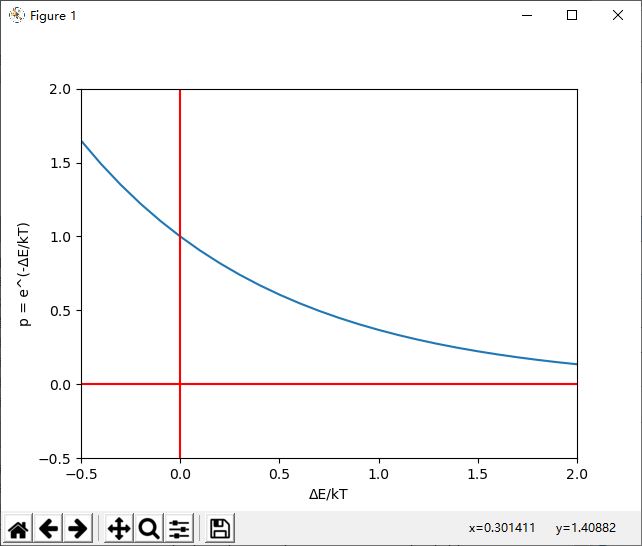
可见，ΔE/kT越小，温度T越高(此时的迭代次数越少)，k越大(人工设置,影响较差解的采纳概率)，ΔE越小(这个较差解与上一个解的差越小)，被采纳的概率也就越大。
ΔE<0，新解更小，采纳它；否则，从(0,1)中随机一个数R，若R<P\(_k\)，则采纳它。

(这个图是求最大)

---

求函数在[0,9]之间的最大值：

import math
import random


def y(x):   # 函数y即能量E
    return x + 10 * math.sin(5 * x) + 7 * math.cos(4 * x)

def is_acceptable(delta_E,tmp,k=1):     # 是否可采纳
    if delta_E<0:   # ΔE<0，直接采纳
        return True

    p=math.exp(-delta_E/(k*tmp))    # 求概率
    if random.random()<p:
        return True
    else:
        return False


left = 0    # 左边界
right = 9   # 右边界

tmp = math.e**5   # 初始温度
tmp_min = math.e**-3    # 停止温度
alpha = 0.98    # 降温系数

x_old = left + random.random() * (right-left)    # 生成初始随机解
E_old = y(x_old)

counter = 0     # 生成更差解的次数


while tmp > tmp_min:
    
    t = (random.random() - 0.5) * 3     # 生成随机解
    x_new= x_old + t
    if x_new<left or x_new>right:
        x_new = x_new - 2*t

    E_new = y(x_new)
    delta_E = -(E_new - E_old)

    if is_acceptable(delta_E,tmp):  # 可采纳
        x_old = x_new
        E_old = E_new

    if delta_E<0:   # ΔE<0，生成更优解，降温
        tmp = tmp * alpha
    else:
        counter += 1

    if counter > 10000:
        break


print('y(' + str(x_old) + ') = ' + str(E_old))

TSP问题：

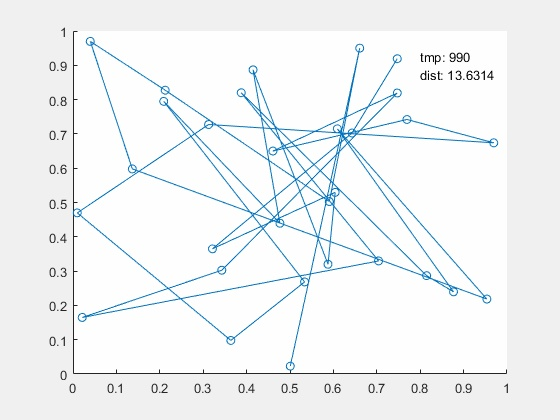
import math
import random

#############################################

def get_all_dist():   # 每两个城市间的距离
    for i in range(len(cities)):
        for j in range(i,len(cities)):
            d[(i,j)] = d[(j,i)] = math.sqrt((cities[i][0]-cities[j][0])**2 + (cities[i][1]-cities[j][1])**2)


def create_new_route(a):     # 产生新路径
    i = random.randint(0,len(a)-1)
    j = random.randint(0,len(a)-1)
    a[i],a[j] = a[j],a[i]


def get_route_dist(a):    # 路径长度即能量E
    dist = 0
    for i in range(len(a)-1):
        dist += d[(a[i],a[i+1])]
    return dist


def is_acceptable(delta_E,tmp,k=1):     # 是否可采纳
    if delta_E<0:   # ΔE<0，直接采纳
        return True

    p=math.exp(-delta_E/(k*tmp))    # 求概率
    if random.random()<p:
        return True
    else:
        return False

#############################################

# 城市坐标
cities = [[1304,2312],[3639,1315],[4177,2244],[3712,1399],[3488,1535],[3326,1556],[3238,1229],[4196,1004],[4312,790],[4386,570],
[3007,1970],[2562,1756],[2788,1491],[2381,1676],[1332,695],[3715,1678],[3918,2179],[4061,2370],[3780,2212],[3676,2578],[4029,2838],
[4263,2931],[3429,1908],[3507,2367],[3394,2643],[3439,3201],[2935,3240],[3140,3550],[2545,2357],[2778,2826],[2370,2975]]
d = dict()   # 每两个城市间的距离
get_all_dist()

route_old = list(range(len(cities)))    # 初始路径
E_old = get_route_dist(route_old)   # 初始路径长度

tmp = math.exp(3)   # 初始温度
tmp_min = math.exp(-8)    # 停止温度
alpha = 0.98    # 降温系数

counter = 0     # 生成更差解的次数

#############################################


while tmp > tmp_min:

    route_new = route_old    
    create_new_route(route_new)     # 生成随机解
    
    E_new = get_route_dist(route_new)
    delta_E = E_new - E_old

    if is_acceptable(delta_E,tmp):  # 可采纳
        route_old = route_new
        E_old = E_new

    if delta_E<0:   # ΔE<0，生成更优解，降温
        tmp = tmp * alpha
    else:
        counter += 1

    if counter > 10000:
        break


print(route_old)
print(E_old)

参考：

• https://zhuanlan.zhihu.com/p/33184423
• https://www.luogu.com.cn/blog/m-sea/qian-tan-SA
• https://www.cnblogs.com/sench/p/9427193.html