对称密钥算法 - AES算法

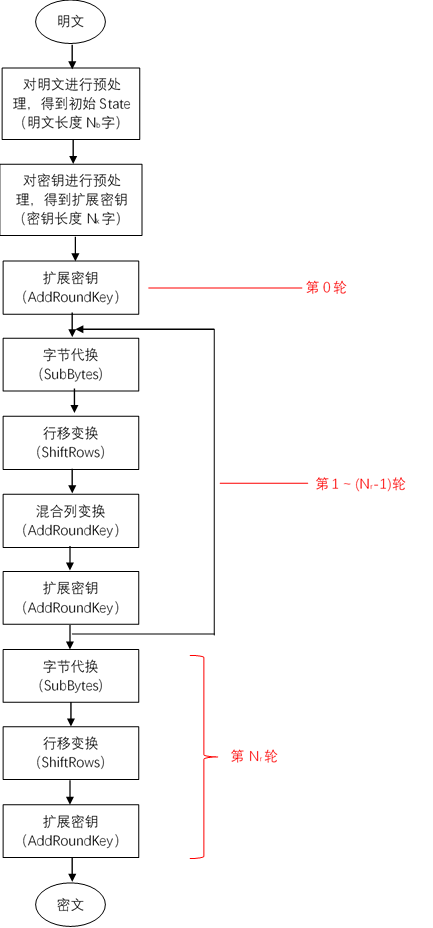
　　　　　　　　　　　　　　　　　　　　　　　　　　　　算法流程图

一、输入明文、密钥

输入明文  ：“00 11 22 33 44 55 66 77 88 99 aa bb cc dd ee ff”

输入密钥k：“00 01 02 03 04 05 06 07 08 09 0a 0b 0c 0d 0e 0f”

可知明文长度N_b=128 bit=32 Byte=4 Word

　　密钥长度N_k=128 bit=32 Byte=4 Word

　　循环轮数N_r的取值=10轮（见下表）

Nr	Nb=4	Nb=6	Nb=8
Nk=4	10	12	14
Nk=6	12	12	14
Nk=8	14	14	14

 

二、对明文数据块做预处理

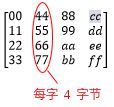
把明文块写成字的形式，每个字包含4个字节，把字节记为列的形式。每个字节是GF(2⁸）域的元素。

三、密钥扩展

将N_k个字长的输入密钥k扩展成长度为N_k(N_r+1)个字的扩展后密钥w。

当N_k<=6时：

　　　　for i := 0~N_k-1

　　　　w[i] = k[i];

　　　　for i := N_k~N_kN_r-1

　　　　w[i] = w[i-1]  XOR  w[i-N_k]　　( i % N_k != 0 )

　　　　w[i] = SubWord( RotWord( w[i-1] ) )  XOR  w[i-N_k]  XOR  Rcon[i/N_k]　　( i % N_k = 0 )

当Nk>6时：

　　　　for i := 0~N_k-1

　　　　w[i] = k[i];

　　　　for i := N_k~N_kN_r-1

　　　　w[i] = w[i-1]  XOR  w[i-N_k]　　( i % N_k != 0 )

　　　　w[i] = SubWord( w[i-1] )  XOR  w[i-N_k]　　( i % N_k = 0 )

 

①RotWord()

将一个4字节的序列[a0,a1,a2,a3]左移一个字节变为[a1,a2,a3,a0].

如：[0c,0d,0e,0f]→[0d,0e,0f,0c]

②SubWord()

将一个4字节的序列[a0,a1,a2,a3]的每一个字节进行S盒变换.

如：0d→d7

　　[0d,0e,0f,0c]→[d7,ab,76,fe]

AES加密的S盒

行/列	0	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
0	0x63	0x7c	0x77	0x7b	0xf2	0x6b	0x6f	0xc5	0x30	0x01	0x67	0x2b	0xfe	0xd7	0xab	0x76
1	0xca	0x82	0xc9	0x7d	0xfa	0x59	0x47	0xf0	0xad	0xd4	0xa2	0xaf	0x9c	0xa4	0x72	0xc0
2	0xb7	0xfd	0x93	0x26	0x36	0x3f	0xf7	0xcc	0x34	0xa5	0xe5	0xf1	0x71	0xd8	0x31	0x15
3	0x04	0xc7	0x23	0xc3	0x18	0x96	0x05	0x9a	0x07	0x12	0x80	0xe2	0xeb	0x27	0xb2	0x75
4	0x09	0x83	0x2c	0x1a	0x1b	0x6e	0x5a	0xa0	0x52	0x3b	0xd6	0xb3	0x29	0xe3	0x2f	0x84
5	0x53	0xd1	0x00	0xed	0x20	0xfc	0xb1	0x5b	0x6a	0xcb	0xbe	0x39	0x4a	0x4c	0x58	0xcf
6	0xd0	0xef	0xaa	0xfb	0x43	0x4d	0x33	0x85	0x45	0xf9	0x02	0x7f	0x50	0x3c	0x9f	0xa8
7	0x51	0xa3	0x40	0x8f	0x92	0x9d	0x38	0xf5	0xbc	0xb6	0xda	0x21	0x10	0xff	0xf3	0xd2
8	0xcd	0x0c	0x13	0xec	0x5f	0x97	0x44	0x17	0xc4	0xa7	0x7e	0x3d	0x64	0x5d	0x19	0x73
9	0x60	0x81	0x4f	0xdc	0x22	0x2a	0x90	0x88	0x46	0xee	0xb8	0x14	0xde	0x5e	0x0b	0xdb
A	0xe0	0x32	0x3a	0x0a	0x49	0x06	0x24	0x5c	0xc2	0xd3	0xac	0x62	0x91	0x95	0xe4	0x79
B	0xe7	0xc8	0x37	0x6d	0x8d	0xd5	0x4e	0xa9	0x6c	0x56	0xf4	0xea	0x65	0x7a	0xae	0x08
C	0xba	0x78	0x25	0x2e	0x1c	0xa6	0xb4	0xc6	0xe8	0xdd	0x74	0x1f	0x4b	0xbd	0x8b	0x8a
D	0x70	0x3e	0xb5	0x66	0x48	0x03	0xf6	0x0e	0x61	0x35	0x57	0xb9	0x86	0xc1	0x1d	0x9e
E	0xe1	0xf8	0x98	0x11	0x69	0xd9	0x8e	0x94	0x9b	0x1e	0x87	0xe9	0xce	0x55	0x28	0xdf
F	0x8c	0xa1	0x89	0x0d	0xbf	0xe6	0x42	0x68	0x41	0x99	0x2d	0x0f	0xb0	0x54	0xbb	0x16

 

③Rcon[]

　　Rcon[i]=[x^i-1,0x00,0x00,0x00]，这里x=(02)

　　于是得到：　　Rcon[1] = [01,00,00,00]

　　　　　　　　　Rcon[2] = [02,00,00,00]

　　　　　　　　　Rcon[3] = [04,00,00,00]

　　　　　　　　　Rcon[4] = [08,00,00,00]

　　　　　　　　　Rcon[5] = [10,00,00,00]

　　　　　　　　　Rcon[6] = [20,00,00,00]

　　　　　　　　　Rcon[7] = [40,00,00,00]

　　　　　　　　　Rcon[8] = [80,00,00,00]

　　　　　　　　　Rcon[9] = [1b,00,00,00]

　　　　　　　　　Rcon[10] = [36,00,00,00]

　　　　　　　　　　　　……

 

这里要将Nk=4（<=6）的输入密钥k=扩展成长度为N_k(N_r+1)=4*（10+1）=44个字的扩展后密钥w[4][44] ：

w[4]=[d7,ab,76,fe]  XOR  [00,01,02,03]  XOR  [01,00,00,00]=[d6,aa,74,fd]

w[6]=[d2,af,72,fa]  XOR  [08,09,0a,0b]=[da,a6,78,f1]

四、加密流程 - 扩展密钥（AddRoundKey）

将第i轮变换后的明文State与轮密钥W[i]异或.

AddRoundKey[i] = State  XOR  W[i]

五、加密流程 - 字节代换（SubBytes)

方法1：S盒置换

　　　　S盒见上面↑

方法2：对State求模逆再进行仿射变换

 

例如：0x19 = 0001 1001 = 1 1001 = x4+x3+1，关于不可约多项式 m(x) = x8+x4+x3+x+1 = 1 0001 1011 的模逆为

　　　1 0001 1011 = 1 1111·1 1001+1100　　（x8+x4+x3+x+1 / x4+x3+1=x4+x3+x2+x+1……x3+x2）

　　　1 1001 = 10·1100+1

　　　1100 = 1100·1

　　　1 = 1 1001-10·1100

　　　　=1 1001-10·（1 0001 1011-1 1111·1 1001）

　　　　=1 1001·（1+10·1 1111）-10·1 0001 1011

　　　∴结果为1+10·1 1111 = 11 1111 = 3f

六、加密流程 - 行移变换（ShiftRows）

Nb (明文长度)	移位值
	C0	C1	C2	C3
4	0	1	2	3
6	0	1	2	3
8	0	1	3	4

例如，当N_b=4时，有：

七、加密流程 - 混合列变换（MixColumns）

例如：

计算[01,02,03,01]·[d4,bf,5d,30]=01·d4+02·bf+03·5d+01·30=66

01=0000 0001　　　　d4=1101 0100

02=0000 0010　　　　bf=1011 1111

03=0000 0011　　　　5d=0101 1101

01=0000 0001　　　　30=0011 0000

这里的加法(+)和乘法(·)都是有限域GF(2⁸)上的，跟普通加法和乘法不一样.

加法(+)  =  异或(⊕)，乘法有两种方法来算

方法1：

01·d4 = d4左移0位(2⁰=1) = 1101 0100

02·bf  = bf 左移1位(2¹=2) = 0111 1110 ，移出去的最高位是1，还要再异或1b(0001 1011) ，0111 1111⊕0001 1011=0110 0101

03·5d = (02+01)·5d = 02·5d+01·5d ， 02·5d = 5d左移1位(2¹=2) = 1011 1010 ，移出去的最高位是0

　　　　　　　　　　　　　　　　　01·5d = 5d左移0位(2⁰=1) = 0101 1101

　　　　　　　　　　　　　　　　　02·5d+01·5d = 1011 1010 ⊕ 0101 1101 = 1110 0111

01·30= 30左移0位(2⁰=1) = 0011 0000

01·d4+02·bf+03·5d+01·30 = 1101 0100⊕0110 0101⊕1110 0111⊕0011 0000 = 0110 0110 = 66

方法2：

01·d4 = 1·（x⁷+x⁶+x⁴+x²）= x⁷+x⁶+x⁴+x²，(x7+x6+x4+x2) mod （x8+x4+x3+x+1）= x7+x6+x4+x2 = 1101 0100

02·bf  = x·（x7+x5+x4+x3+x2+x+1）= x8+x6+x5+x4+x3+x2+x，(x8+x6+x5+x4+x3+x2+x) mod （x8+x4+x3+x+1）= x6+x5+x2+1 = 0110 0101

03·5d =（x+1）·（x6+x4+x3+x2+1）= x7+x6+x5+x2+x+1，(x7+x6+x5+x2+x+1) mod （x8+x4+x3+x+1）= x7+x6+x5+x2+x+1 = 1110 0111

01·30 = 1·（x5+x4）= x5+x4，（x5+x4） mod （x8+x4+x3+x+1）= x5+x4 = 0011 0000

01·d4+02·bf+03·5d+01·30 = 1101 0100⊕0110 0101⊕1110 0111⊕0011 0000 = 0110 0110 = 66