计算复杂性（第一章）

前言：学习笔记对应的书籍为 Sanjeev Arora and Boaz Barak 的 Computational Complexity: A Modern
Approach，可以在这里下载电子书的 pdf 文件。也可以加我的 qq 2589436581 讨论书籍和笔记的内容。

第一章 计算模型

1.1 一些约定

设 $f$ 是从 01 字符串到 01 输出的函数，称其为 01 函数。这个函数可以用一个集合 $L(f)=\{x:f(x)=1\}$ 来描述，并把这个集合叫做语言或者决策问题（decision problems）。

记号：$\langle x,y\rangle$ 表示一个二元组。

举个例子：对于无向图的最大独立集问题，它对应的语言就是 $\text{INDSET}=\{\langle G=(V,E),k\rangle: \exists S \subset V\ \text{s.t.} |S|\geq k \ \text{and} \ \forall x,y\in S (x,y)\notin E\}$。

记号：$\llcorner \cdot \lrcorner$ 表示 $\cdot$ 的二进制表示。

对于一个算法，一般用 $T(n)$ 表示再输入长度为 $n$ 的前提下，算法运行完毕所需要的最大基本操作次数。

复杂度记号：$f=O(g)$ 表示 $f$ 不超过 $g$ 的阶，$f=\Omega(g)$ 反之，$f=\Theta(g)$ 表示 $f$ 与 $g$ 同阶，$f=o(g)$ 表示 $f$ 的阶低于 $g$，$f=w(g)$ 反之。

1.2 对计算和效率建立模型

先来一个不太严谨的说法：对于一个 $f$ 的算法就是一系列规则。每条规则必须是固定的，但是对规则的使用次数没有限制。每条规则涉及以下一种或多种基本操作：

1. 从输入（input）读一个 bit。

2. 从写字板（scratch pad）或者一个工作空间（working space）读一个 bit。

3. 根据读入的结果，在写字板上写一个 bit。

4. 根据读入的结果，或是停止并输出答案 0/1，或是选择下一条需要使用的规则并继续。

注意：任何给定的字符集都可以和固定长度的 0/1 字符串构造双射，所以上文中的一个 bit 也可以是某个给定的字符集中的一个字符。

1.2.1 图灵机（Turing Machine，简称 TM）

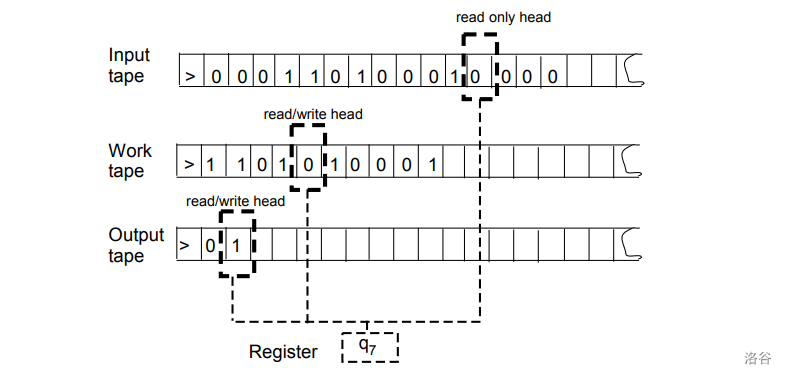
$k-$纸带图灵机是上文不严谨的说法的一个具体实现。它有一个字符集 $\Gamma$。纸带全部都是单向的（这里没搞懂单向的意义，也可能是我理解错了，原文 A tape is an infinite one-directional line of
cells...），有无穷个单元，每个单元可以存放一个 $\Gamma$ 中的字符。每个纸带还有一个带头，可以每次对单元写入或读入一个字符，也可以左右移动。

第一个纸带是输入纸带，不允许写入字符。其他 $k-1$ 个纸带叫做工作纸带，可读可写。最后一个纸带还是输出纸带，输出最终答案。

图灵机有一个有限的状态集合 $Q$，以及一个可以用于存放一个状态的寄存器（register），表示当前所处状态。当前状态决定了下一步要进行的操作，操作分为以下几种：

1. 读入 $k$ 个带头下面的字符。

2. 对于可写的 $k-1$ 个纸带，同时在每个带头下面写入新的字符（如果你想保持不变的话，就写入与之前相同的字符）。

3. 改变寄存器里的状态。

4. 将每个带头向左或向右移动或者不动。

图灵机的严格定义：

一个 TM 可以用三元组 $\langle \Gamma, Q, \delta\rangle$ 描述。

$\Gamma$ 是一个字符集。一般假设其中至少有一个表示空的字符 $\square$，和一个表示开始的字符 $\triangle$ 和数字 $0,1$。

$Q$ 是一个状态集。一般假设其中至少包括一个 $q_{start}$ 和一个 $q_{halt}$。

$\delta$ 是一个函数，描述 $Q\times \Gamma^k \to Q\times \Gamma^{k-1}\times \{L,S,R\}^k$ 的映射。这个链接 里说一般的图灵机是不允许 $S$（stay）的，只有 $\{L,R\}$，只有一些变体允许 $S$。这本书之前说必须左移或右移，这里又写了 $S$，只能说作者太不仔细了，当然这并不影响图灵机的本质。

TM 的初始配置（configuration）是这样的：所有带头在最左端，每个纸带最左端是 $\triangle$，读入纸带的后面是输入内容，再后面为空；其他纸带的后面为空。初始状态在 $q_{start}$。当状态到达 $q_{halt}$ 时即停机。在复杂性理论中，我们只关心对于所有输入都在有限步内停机的算法。

接下来我们正式地定义算法的运行时间。如果对于任意输入 $x$，一个 $f$ 的算法 $M$ 能在 $T(|x|)$ 步以内停机并正确输出 $f(x)$，则称 $M$ 能以 $T-$ 时间计算 $f$。

时间可构函数：对于 $T:\mathbb{N}\to \mathbb{N}$，若 $T(n)\geq n$，且存在图灵机 $M$ 能以 $T-$ 时间计算 $x\to \llcorner T(|x|)\lrcorner$ 的函数，则称 $T(n)$ 是时间可构的。

白话理解是：如果计算出 $T(n)$ 的复杂度都不止 $O(T(n))$，那么这个复杂度就没有意义了。

1.2.2 图灵机定义的鲁棒性

注意到关于图灵机的许多定义是非常随意的。对工作纸带的数量 $k$ 没有特别规定；对字符集 $\Gamma$ 的大小没有规定，只要求必须含有 $\{\square,\triangle,0,1\}$，对纸带是否是双向无限长的都没有限制。这是因为可以证明能在 $k-$ 纸带图灵机上以 $T(n)$ 运行的算法一定可以以不超过 $CkT^2(n)$ 的操作次数在 $1-$ 纸带图灵机上运行；双向无限长的纸带上的 $T(n)$ 可以转化为在单向无限长的纸带上的 $T^2(n)$，$|\Gamma|$ 大小的字符集上的 $T(n)$ 可以转化为 $\{\square,\triangle,0,1\}$ 上的 $C|\Gamma|T(n)$ 等等。这些证明都不难，所以就略去了。

Rmk. 纸带头的移动方式只和读入的长度有关，而与读入的内容无关的图灵机叫做健忘的图灵机（oblivious TM）。事实上，所有图灵机都可以被健忘的图灵机模拟。

1.2.3 图灵机的强大表达能力

图灵机可以模拟任意一个编程语言的任意一个程序；同时，大多数编程语言也可以模拟一台图灵机。

1.3 图灵机的字符串表示和通用图灵机

因为图灵机的字符集和状态集都是有限的，并且可以用转移函数来完整地描述这个图灵机，所以一定可以用一个 0/1 字符串来表示图灵机。同时，一个图灵机也可以被无限个 0/1 字符串表示（在末尾添加任意个无用的 1 即可，类似于程序的注释）。

下文中用 $\llcorner M \lrcorner$ 表示图灵机 $M$ 的字符串表示，$M_\alpha$ 表示 $\alpha$ 这个字符串所代表的图灵机。

1.3.1 通用图灵机

通用图灵机 $N$ 可以以任意一个图灵机 $M$ 作为输入来模拟这个图灵机。严谨来说，

Thm.（高效通用图灵机）存在图灵机 $N$，对于任意 $x,\alpha\in\{0,1\}^{*}$，有 $N(x,\alpha)=M_{\alpha}(x)$。或者说，如果 $M_{\alpha}$ 对于一个 $x$ 能在 $T$ 步内停机，那么 $N$ 将在至多 $CT\log T$ 步内停机，其中 $C$ 是一个只和 $M_{\alpha}$ 的各个参数相关的常数。

这个证明是比较 trivial 的。不妨设 $M_{\alpha}$ 只有一个工作纸带，那么只需要令 $N$ 有一个功能和 $M_{\alpha}$ 完全相同的工作纸带，以及一个写有所有转移函数的信息的工作纸带和一个表示 $M_{\alpha}$ 当前所处的状态就可以了。

Rmk.（没看懂）考虑给 $N$ 额外加入一个输入 $t$，并让 $N$ 维护一个计数器，当且仅当 $M_{\alpha}$ 在 $t$ 步内停机时输出 $M_{\alpha}(x)$，否则输出一个表示失败的符号。然后上面的证明可以小改一下给出具有同样复杂度的通用图灵机。（原文 It is sometimes useful to consider a variant of the universal TM $U$ that gets a number $t$ as an
extra input (in addition to $x$ and $\alpha$), and outputs $M_{\alpha}(x)$ if and only if $M_{\alpha}$ halts on $x$ within $t$
steps (otherwise outputting some special failure symbol). By adding a counter to $U$, the proof of
Theorem 1.13 can be easily modified to give such a universal TM with the same efficiency.）

1.4 不可计算的函数

Thm. 存在函数 $UC:\{0,1\}^{*}\to \{0,1\}$ 不可被任何 TM 计算，即任何 TM 都无法对任意合法输入都在有限步内停机并得出正确结果。

Proof. 令 $UC(\alpha)$ 表示以 $M_{\alpha}(\alpha)$ 是否会在有限步内停机并输出 $1$，如果是，则 $UC(\alpha)=0$，否则 $UC(\alpha)=1$。假设有一个图灵机 $N$ 可以计算这个函数 $UC$，注意到 $\exists \beta:N=M_{\beta}$，然而根据定义 $N(\beta)=UC(\beta)\neq M_{\beta}(\beta)$ ，产生了矛盾，所以这个 $UC$ 是一个确实存在但不可能被计算出来的函数。

Rmk 1. 这个证明方法叫做“对角线法”（diagnoalization）

Rmk 2. 这里逻辑是没有问题的，我最初的理解不够深刻。当我们确定图灵机的编码规则之后，生成了一系列图灵机 $M_{\alpha},\alpha\in\{0,1\}^*$，自然 $UC$ 函数的所有点值都已经确定了。这些图灵机都有某种计算功能，我们称图灵机 $M$ 能计算 $f$ 当且仅当 $\forall \alpha\in\{0,1\}^*:f(\alpha)=M(\alpha)$，这个证明是在说：不存在能在所有输入上都和 $UC$ 相等的图灵机。

当然这个函数太奇怪了，我们应该也不会想要去计算它。所以接下来我们将看到另一个有实际意义的不可计算函数：停机函数 $\text{H}$，它实际上是前面的 $UC$ 函数的一个更一般化的函数。

1.4.1 停机问题

停机问题以 $\alpha,x$ 两个参数作为输入，输出 $M_{\alpha}(x)$ 是否会在有限步内结束，分别用 1/0 表示，下文不再重述。

Thm. $\text{H}$ 不可被任何 $TM$ 计算。

Proof. 假设存在图灵机 $M$ 可以计算 $\text{H}$，记其为 $M_{\text{H}}$。那么对于之前提到的 $UC$ 函数，我们可以如此构造一个可以计算 $UC$ 函数的图灵机 $N$：对于一个输入 $\alpha$，如果 $M_{H}(\alpha,\alpha)=0$，那么输出 $0$，否则运行通用图灵机 $K$，计算 $M_{\alpha}(\alpha)$，输出 $1-M_{\alpha}(\alpha)$。这与之前得到的“$UC$ 函数不可被计算”的结论矛盾。

Rmk. 这个证明方法叫“规约”（reduction），意思是如果一个能解决问题 $A$ 的方法能被简单改造后解决问题 $B$，那么问题 $A$ 至少是不弱于问题 $B$ 的。

1.5 确定性时间和 $\text{P}$ 类问题

使用某个给定资源可以计算的函数构成的集合叫做一个复杂度类。

Def.（DTIME 类）设 $T:\mathbb{N}\to \mathbb{N}$ 是一个函数。可以用 $c\times T(n)$ 的时间计算的 01 函数（$c$ 是一个大于 $0$ 的常数）构成的集合记作 $\text{DTIME}(T(n))$。

Def.（$\text{P}$ 类）$\text{P}=\displaystyle\bigcup_{c\geq 1}\text{DTIME}(n^c)$

关于 $\text{P}$ 类问题的定义有一些经典的质疑：

1. 要求最坏复杂度不超过多项式级别是否过于严苛？此外，有时求出近似解的复杂度会远远低于求出精确解的高复杂度，此时能否对 $\text{P}$ 给出另外一种合理的定义？

2. 在不同计算模型上的 $\text{P}$ 类问题集合是否相同？

Hypothesis.（Church-Turing 命题）所有物理上可以实现的计算模型都可以用图灵机来模拟。

Hypothesis.（加强版 Church-Turing 命题）所有物理上可以实现的计算模型都可以用图灵机来模拟，并且其每一步操作都可以转化为图灵机上的关于 $n$ 的多项式步操作。

如果这个命题成立的话，所有计算模型上的 $\text{P}$ 类问题集合全部相同。

但是：

（1）精度问题。图灵机涉及的东西都是离散的，而现实世界是连续的，所以图灵机真的什么都能模拟吗？

（2）随机数能否加快图灵机的速度？

（3）量子计算。现在确切地存在一些问题是量子计算意义下的 $\text{P}$ 但不是图灵机意义下的 $\text{P}$，但是量子计算机到底能不能在物理上造出来并不清楚。

（4）其他算法 $\dots$

3. 有些计算问题并不能简单转化为判定问题（或者可能代价过高）。

章节总结：我们学了什么？

1. 计算模型很多，我们用图灵机作为代表，因为我们假定所有计算模型的能力是等价的；

2. 图灵机可以用 0/1 字符串表示，所以存在一个可以模拟任意图灵机的通用图灵机；

3. 存在一些不可能被图灵机计算出来的函数，如 $\text{H}$ 函数；

4. 我们认为 $\text{P}$ 类问题是可以高效解决的，因为图灵机的各类参数，如纸带数量，字符集大小等等不会改变 $\text{P}$ 所包含的问题，所以这些参数都是无所谓的，我们证明一些命题的时候一般选取最符合我们要求的参数。

习题：

Exercise 8.

Question：证明 oblivious TM 的可行性，oblivious TM 的纸带头的位置只和输入的长度和经过的步数相关。具体来说，证明任意一个能在任意一个图灵机上以 $T(n)$ 运行的算法必然能在 oblivious TM 上以 $CT^2(n)$ 运行。

Answer：这个看起来挺怪的，其实不难。不妨假设工作纸带只有 $1$ 条，并且是单向的，设原来的图灵机是 $M$，新造的 oblivious TM 是 $M'$，我们考虑在状态里额外维护一个 $t$，表示当前状态下，如果是在 $M$ 中，下一个要读取的位置在哪里。在 $M$ 中的每次移动一格纸带头的操作，在 $M'$ 中都改成扫描纸带向右 $T(n)$ 格的所有格子，通过 $t$ 来判断哪一位的信息是真正要读取进来的。因为原本的复杂度是 $T(n)$，所以新的复杂度不超过 $CT^2(n)$。

Exercise 9.

Question：证明 Exercise 8 的加强版：把 $CT^2(n)$ 改进到 $CT(n)\log(n)$。

书中给出了一个建造复杂度不超过 $O(T(n)\log T(n))$ 的通用图灵机的方法：

先假设原来的图灵机 $M$ 只有 $1$ 条纸带（否则可以通过扩充字符集来代替多条纸带），然后我们建造的通用图灵机 $N$ 也只有 $1$ 条纸带，字符集中有一个特殊符号 $t$ 表示空白。这条纸带不妨设它是双向的，在正半轴上维护若干区间 $R_i=[2^i,2^{i+1}-1]$，在负半轴上 $L_i=[-2^{i+1}+{1},-2^i]$，和一个原点 $0$。这里 $i$ 不超过 $\log T+O(1)$。我们还是把原来纸带上要写的东西按顺序写在这些区间里，只是未必连着写：时刻保证 $0$ 这个位置有我们正在读入的字符，其他每个区间要么全满，要么全空白，要么恰好一半是有意义的字符，一半是空白。并且，$L_i,R_i$ 这两个区间的字符加起来正好是 $2^i$ 个有意义的字符。初始状态下可以使所有区间都半满，多出来的用任意非空白的字符填上就行。

如此一来我们要进行纸带头向右移动 $1$ 个单位的操作的时候，本质上就是让纸带上的有效字符都向左移动 $1$ 个单位。现在跑得慢的原因是原本纸带头的移动一次的时候，现在都要把所有字符移动一位，复杂度直接乘上 $T(n)$。可以这样做：先找到最小的 $i$ 满足 $R_i$ 不是全空。然后将 $R_i$ 最靠左的 $1$ 个字符移动到 $0$，接下来靠左的 $2^{i-1}-1(i\geq 1)$ 个字符放到 $R_0,R_1,\cdots R_{i-1}$ 里面使得每个半满。把 $L_i$（如果非空的话）的 $2^{i-1}$ 个有意义字符都移到最靠左的 $[-2^{i+1}+1,-2^i-2^{i-1}]$，再把 $0,L_0,L_1,\cdots L_{i-1}$（这些之前全满）里的靠左的 $2^{i-1}$ 个字符左移到 $L_i$ 中靠右的部分 $[-2^i-2^{i-1}+1,-2^i]$，最后把 $0,L_0,L_1,\cdots L_{i-1}$ 中剩余的字符往 $L_0,L_1,\cdots L_{i-1}$ 按照原来的顺序各填一半就可以了。注意我们的操作维持了我们需要维护的性质。并且，搞完一次 $R_i$ 后，虽然我们大概用了 $2^i$ 步操作，但是此时 $L_i,L_{i-1}\cdots L_0,R_0,R_1,\cdots R_{i}$ 都已经是半满状态了，再想要操作到 $R_i$，至少要再经过大约 $2^i$ 步才可以。也就是说总共的步数大概是 $O(\displaystyle\sum_{i=0}^{\log T}2^i\times \frac{T}{2^i}=T\log T)$。

但是书里给的这个方法细节上有问题：$L_0,R_0$ 长度都是 $1$，没法拿出一半。这个细节需要修正，也肯定可以修正，但是真的太烦了，我觉得只要知道核心思路是倍增就好了。这种图灵机的证明细节和实现细节都是重量级，真要写个 C++ 程序模拟这种转化 + 抽象了很多次的通用图灵机能把这世界上最能写的代码手整自闭。所以啊，图灵机这东西还是停留在理论上就够了，用已经封装好的现代计算机写高级语言它不香吗？？？

不过其实还没结束呢。这我们只是造出了一个 $T\log T$ 的通用图灵机，怎么转化成一个能执行某个算法的 oblivious TM 呢？

破防了，大家看看这个 lecture notes 吧，反正我摆烂了

Exercise 15.

设 partial function $f$ 是定义在 $\{0,1\}^*$ 的一个子集 $S$ 上的值域为 $\{0,1\}^*$ 的函数，称图灵机 $M$ 能计算 $f$，当且仅当 $f(x)$ 有定义时 $f(x)=M(x)$，$f(x)$ 无定义时 $M(x)$ 永不停机对所有 $x\in\{0,1\}^*$ 成立。定义 $S$ 是一些这样的 $f$ 构成的集合，定义 $f_S(\alpha)=1$ 当且仅当 $M_{\alpha}$ 能计算 $S$ 中的某一个函数，否则 $f_S(\alpha)=0$。

Thm.（Rice's Theorem）当 $S$ 不平凡，即 $S$ 不为空集或全集时，$f_S$ 不可计算。

Question：

（1）用 Rice's Theorem 证明停机函数 $\text{H}$ 不可计算。

如果 $\text{H}$ 可以计算，那么对于给定的一个 $S$ 中的每个元素（函数）$g$（注意到 $S$ 是可数集），设计这样一个图灵机 $N_g$：给定一个输入 $\alpha$，依次跑遍所有 $\{0,1\}^*$ 中的字符串 $t$，比较 $M_{\alpha}(t)$ 是否和 $g(t)$ 相符。即，如果 $g(t)$ 没有定义，用停机函数 $\text{H}$ 计算 $M_{\alpha}(t)$ 是否会停机；如果 $g(t)$ 有定义，先检查 $M_{\alpha}(t)$ 是否会停机，如果不会停机的话，再计算 $M(t)$。中间任何一步如果发现 $M_{\alpha}(t)$ 的行为与 $g(t)$ 不相符，立刻停机。这一过程保证了如果 $M_{\alpha}(t)$ 和 $g(t)$ 永远相符，则 $N_g$ 在输入 $\alpha$ 上不会停机；否则一定停机。再基于此设计一个图灵机 $K$，$K$ 得到一个输入 $\alpha$，依次跑遍所有 $S$ 中的元素 $g$，用停机函数 $\text{H}$ 计算 $N_g(\alpha)$ 是否会停机。如果在某个 $N_g$ 上不停机，则停机并输出 $1$。根据定义这个 $K$ 可以计算 $f_S$，与 Rice's Theorem 产生矛盾，故 $\text{H}$ 不可计算。

（2）证明 Rice's Theorem。

反证法。假设 Rices's Theorem 是错误的，即存在一族函数 $S$，满足 $f_S$ 可以被计算。不妨设 $S$ 中不存在 $\emptyset$ 函数，$\emptyset$ 函数的定义域是空集。若不然，可以将 $S$ 变成 $S$ 对全体函数的补集，在这两个集合上做判定显然是等价的。并且因为 $S$ 非空非满，所以还存在一个函数 $f\notin S$。接下来我们这样构造一个计算 $\text{H}$ 函数的图灵机 $K$：输入参数 $\alpha,x$，再构造一个图灵机 $N$，$N$ 输入一个参数 $y$，执行的操作是先模拟一遍 $M_{\alpha}(x)$，再根据 $f(y)$ 是否存在选择输出 $f(y)$ 或死循环。$K$ 执行的操作是求出 $f_S(N)$。由于 $M_{\alpha}(x)$ 是一个确定的图灵机 + 输入，我们来考虑 $N$ 的实际功能只可能有两种：要么 $M_{\alpha}(x)$ 停机，那么 $N$ 能计算 $f$，此时 $f_S(N)=0$；要么 $M_{\alpha}(x)$ 不停机，那么 $N$ 就是一个对任何输入都不停机的图灵机，能计算 $\emptyset$，此时 $f_S(N)=1$。所以根据 $f_{S}(N)$ 我们能够判定 $M_{\alpha}(x)$ 是否会停机，这与之前得出的停机函数不可计算的结论产生了矛盾，假设不成立。