聚类--K均值算法

 

1.用python实现K均值算法

K-means是一个反复迭代的过程，算法分为四个步骤：

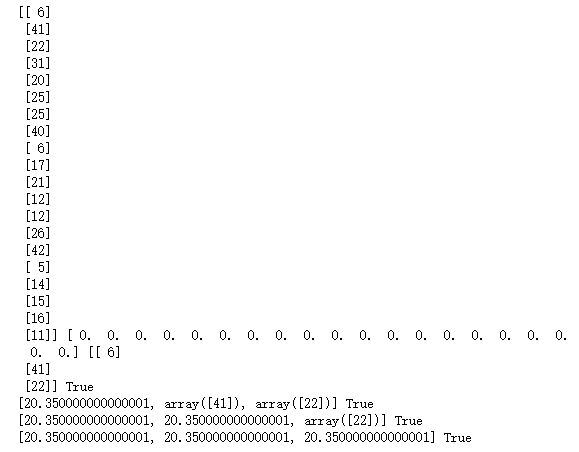
import numpy as np
x = np.random.randint(1,50,[20,1])
y = np.zeros(20)
k = 3
#1） 选取数据空间中的K个对象作为初始中心，每个对象代表一个聚类中心；
def initcen(x,k):
    return x[:k]
#2） 对于样本中的数据对象，根据它们与这些聚类中心的欧氏距离，按距离最近的准则将它们分到距离它们最近的聚类中心（最相似）所对应的类；
def nearest(kc,i):
    d = abs(kc-i)
    w = np.where(d == np.min(d))
    return w[0][0]

def xclassify(x,y,kc):
    for i in range(x.shape[0]):
        y[i] = nearest(kc,x[i])
        return y

#3） 更新聚类中心：将每个类别中所有对象所对应的均值作为该类别的聚类中心，计算目标函数的值；

def kcmean(x,y,kc,k):
    l = list(kc)
    flag = False
    for c in range(k):
        m = np.where(y ==0)
        n = np.mean(x[m])
        if l[c] != n:
            l[c] = n
            flag = True
            print(l,flag)
    return (np.array(l),flag)
#4） 判断聚类中心和目标函数的值是否发生改变，若不变，则输出结果，若改变，则返回2）
kc = initcen(x,k)

flag = True
print(x,y,kc,flag)
while flag:
    y = xclassify(x,y,kc)
    kc,flag = kcmean(x,y,kc,k)
print(y,kc)

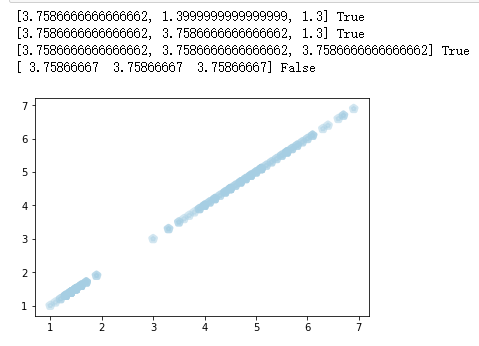
2. 鸢尾花花瓣长度数据做聚类并用散点图显示。

from sklearn.datasets import load_iris
iris = load_iris()
datas = iris.data
iris_length=datas[:,2]

# 用鸢尾花花瓣作分析
x = np.array(iris_length)
y = np.zeros(x.shape[0])
kc = initcen(x,3)
flag = True
while flag:
    y = xclassify(x,y,kc)
    kc,flag = kcmean(x,y,kc,3)
print(kc,flag)

# 分析鸢尾花花瓣长度的数据，并用散点图表示出来
import matplotlib.pyplot as plt
plt.scatter(iris_length, iris_length, marker='p', c=y, alpha=0.5, linewidths=4, cmap='Paired')
plt.show()

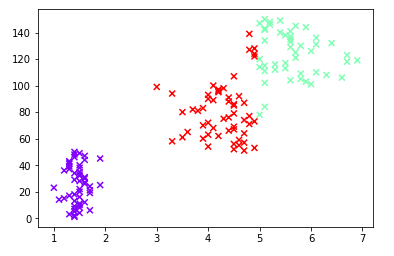
3. 用sklearn.cluster.KMeans，鸢尾花花瓣长度数据做聚类并用散点图显示.

from sklearn.cluster import KMeans

iris_length = datas[:, 2:3]
k_means = KMeans(n_clusters=3)
result = k_means.fit(iris_length)
kc1 = result.cluster_centers_
y_kmeans = k_means.predict(iris_length)

# 画图
plt.scatter(iris_length,np.linspace(1,150,150),c=y_kmeans,marker='x',cmap='rainbow',linewidths=4)
plt.show()

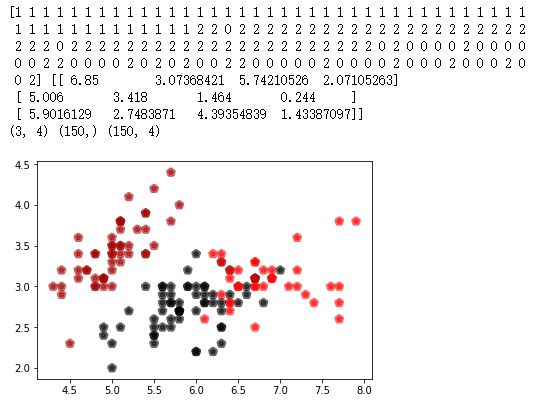
4. 鸢尾花完整数据做聚类并用散点图显示.

k_means1 = KMeans(n_clusters=3)
result1 = k_means1.fit(datas)
kc2 = result1.cluster_centers_
y_kmeans1 = k_means1.predict(datas)

print(y_kmeans1, kc2)
print(kc2.shape, y_kmeans1.shape, datas.shape)

plt.scatter(datas[:, 0], datas[:, 1], c=y_kmeans1, marker='p', cmap='flag', linewidths=4, alpha=0.6)
plt.show()