python C3算法
Python MRO
C3算法是python当中计算类继承顺序的一个算法,从python2.3以后就一直使用此算法了。
c3 linearization算法称为c3线性化算法
C3算法原理
首先定义几个符号的意义:
| 符号 | 意义 |
|---|---|
| L | 针对一个类进行解析用L进行表示,例如L(A)表示对类A进行解析 |
| merge | 合并操作的一个函数(后面具体介绍) |
| C | 表示一个类名 |
| B | 表示是C的一个子类,如果多个子类用B1,B2....表示 |
| + | 元素列表顺序添加 |
| tail | 去除列表第一个元素,例如 tail([1,2,3,4]) = [2,3,4] |
L(C) = C + merge(L(B1) + L(B2) + ...+ )
merge函数合并规则:
- 首先选中merge 函数的第一个参数(也是一个列表),按照公式里的描述就是L(B1)。
- 取列表中第一个元素记为h,如果h没有出现其他 列表的
tail中, 那么将其移到 merge函数前,提取出来,并且将这个元素在所有列表中移除,并重复 2。 - 如果出现在其他列表中的
tail中,寻找下一个列表。 - merge 函数所有元素都被移除类创建成功,如果寻找不到下一个列表则创建失败。
下面举例说明:
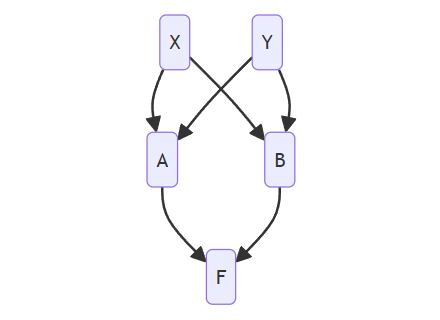
class X():
pass
class Y():
pass
class A(X, Y):
pass
class B(X, Y):
pass
class F(A, B):
pass
print(F.__mro__)
我们来解析 F的mro顺序,则首先记为 L(F),根据
L(C) = C + merge(L(B1) + L(B2) + ...+ )
公式得到:
L(F) = F + merge(L(A)+L(B))
接下来计算L(A),与L(B):
L(A) = A + merge(L(X),L(Y)) = A + merge([X],[Y]) = [A,X,Y]
L(B) = B + merge(L(X),L(Y)) = B + merge([X],[Y]) = [B,X,Y]
带入 L(F) = L(F) + merge(L(A)+L(B)) 得到:
L(F) = F + merge([A,X,Y],[B,X,Y])
下面是关键merge逻辑理解了,首先根据 merge 的说明 1,选中得到 [A,X,Y], 根据merge的说明2,选中第一个元素 A, 判断A 是否在 tail(B,X,Y) 中,即 A 是否在 [X,Y] 中,不在,将其提出来,得到:
L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y])
接着重复 merge的2,判断 X 是否在 tail(B,X,Y)=[X,Y] 中,结果是存在,那么寻找[X,Y]的下一个列表,即[B,X,Y],判断B 是否存在 tail([X,Y])=[Y] 中,不存在,提出B,得到:
L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y]) = [F,A,B] + merge([X,Y],[X,Y])
剩下逻辑一样,依次提出 X和Y:
L(F) = F + merge([A,X,Y],[B,X,Y]) = [F,A] + merge([X,Y],[B,X,Y]) = [F,A,B] + merge([X,Y],[X,Y]) = [F,A,B,X,Y]
可以将我上述python代码运行一下结果和我们手算的是一样的:
(<class '__main__.F'>, <class '__main__.A'>, <class '__main__.B'>, <class '__main__.X'>, <class '__main__.Y'>, <class 'object'>)
复杂的解析(练手逻辑)
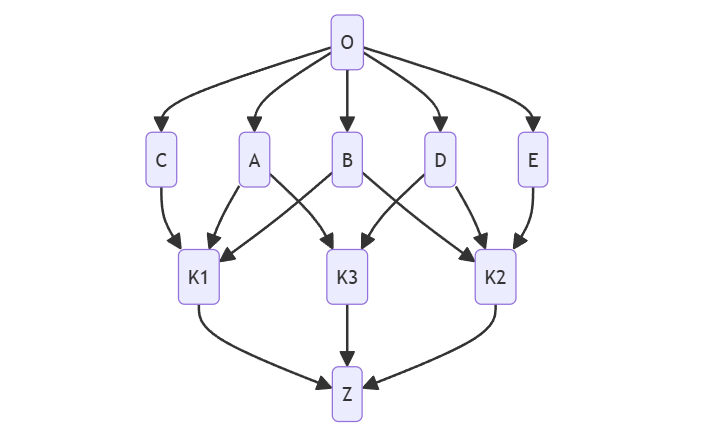
L(K1) = K1 + merge(L(C), L(A), L(B))
= K1 + merge([C, O], [A, O], [B, O])
= [K1, C] + merge([O], [A, O], [B, O])
= [K1, C, A] + merge([O], [O], [B, O])
= [K1, C, A, B] + merge([O], [O], [O])
= [K1, C, A, B, O]
L(K2) = [K2, B,D,E, O]
L(K3) = [K3,A, D, O]
L(Z) = Z + merge(L(K1), L(K3), L(K2))
= Z + merge([K1, C, A, B, O],[K3, A, D, O],[K2, B, D, E, O])
= [Z, K1] + merge([C, A, B, O], [K3, A, D, O], [K2, B, D, E, O])
= [Z, K1, C] + merge([A, B, O], [K3, A, D, O], [K2, B, D, E, O])
= [Z K1, C] + merge([A, B, O], [K3, A, D, O], [K2, B, D,E, O])
= [Z, K1, C, K3] + merge([A, B, O], [A, D, O], [K2, B, D, E, O])
= [Z, K1, C, K3, A] + merge([B, O], [D, O], [K2, B, D, E, O])
= [Z,K1, C, K3, A, K2] + merge([B, O], [D, O], [B, D, E, O])
= [Z,K1, C, K3, A, K2, B] + merge([O], [D, O], [D, E, O])
= [Z, K1,C, K3, A, K2, B, D] + merge([O], [O], [E,O])
= [Z, K1,C, K3, A, K2, B, D, E, O]
class O:
pass
class C(O):
pass
class A(O):
pass
class B(O):
pass
class D(O):
pass
class E(O):
pass
class K1(C,A,B):
pass
class K3(A,D):
pass
class K2(B,D,E):
pass
class Z(K1,K3,K2):
pass
print(Z.__mro__)
手写C3算法
def c3MRO(cls):
if cls is object:
# 讨论假设顶层基类为object,递归终止
return [object]
# 构造C3-MRO算法的总式,递归开始
mergeList = [c3MRO(baseCls) for baseCls in cls.__bases__]
mergeList.append(list(cls.__bases__))
mro = [cls] + merge(mergeList)
return mro
def merge(inLists):
if not inLists:
# 若合并的内容为空,返回空list
# 配合下文的排除空list操作,递归终止
return []
# 遍历要合并的mro
for mroList in inLists:
# 取head
head = mroList[0]
# 遍历要合并的mro(与外一层相同),检查尾中是否有head
### 此处也遍历了被取head的mro,严格地来说不符合标准算法实现
### 但按照多继承中地基础规则(一个类只能被继承一次),
### head不可能在自己地尾中,无影响,若标准实现,反而增加开销
for cmpList in inLists[inLists.index(mroList) + 1:]:
if head in cmpList[1:]:
break
else:
# 筛选出好head
nextList = []
for mergeItem in inLists:
if head in mergeItem:
mergeItem.remove(head)
if mergeItem:
# 排除空list
nextList.append(mergeItem)
# 递归开始
return [head] + merge(nextList)
else:
# 无好head,引发类型错误
raise TypeError
参考文章:


