108.奇数码问题
原题链接:108. 奇数码问题

解题思路
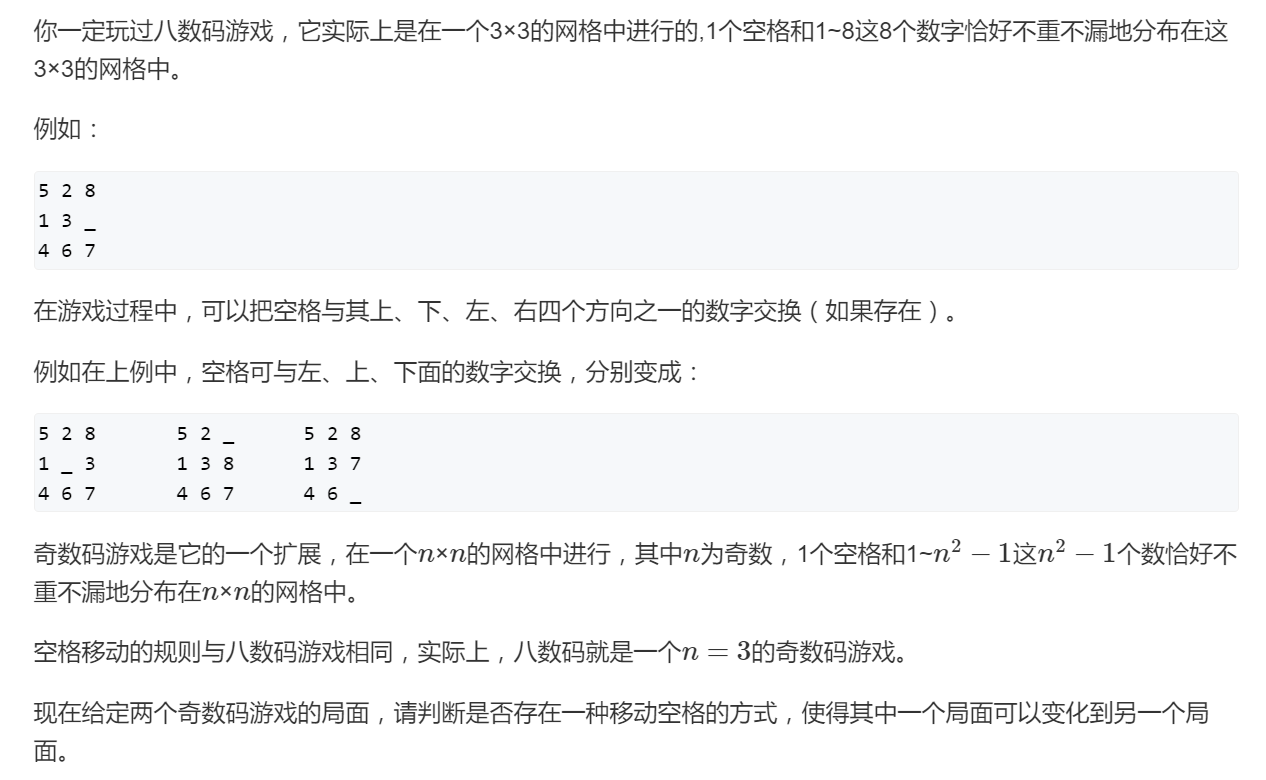
奇数码问题两个局面可以达成,当且仅当两个局面下网格中的数以此写成1行 n*n-1 个元素的序列后(不考虑空格),逆序对个数的奇偶性相同。例如题目描述中的第一个局面可以写成[5 2 8 1 3 4 6 7]。该结论的必要性很容易证明:空格左右移动时,写数交换了位置,因为n-1是偶数,所以逆序对数的变化也只能是偶数。
上面的结论还可以扩展到n为偶数的情况,此时两个局面可达,当且仅当两个局面对应网格写成序列后,“逆序对数之差”和“两个局面下空格所在行数之差”奇偶性相同。事实上,在n*m网格中(n,m>=2)也服从上述的两个结论之一(根据列数奇偶性分情况讨论)。
总而言之,n*m数码问题的有解性判定,可以转化为归并问题排序就逆序对来解决
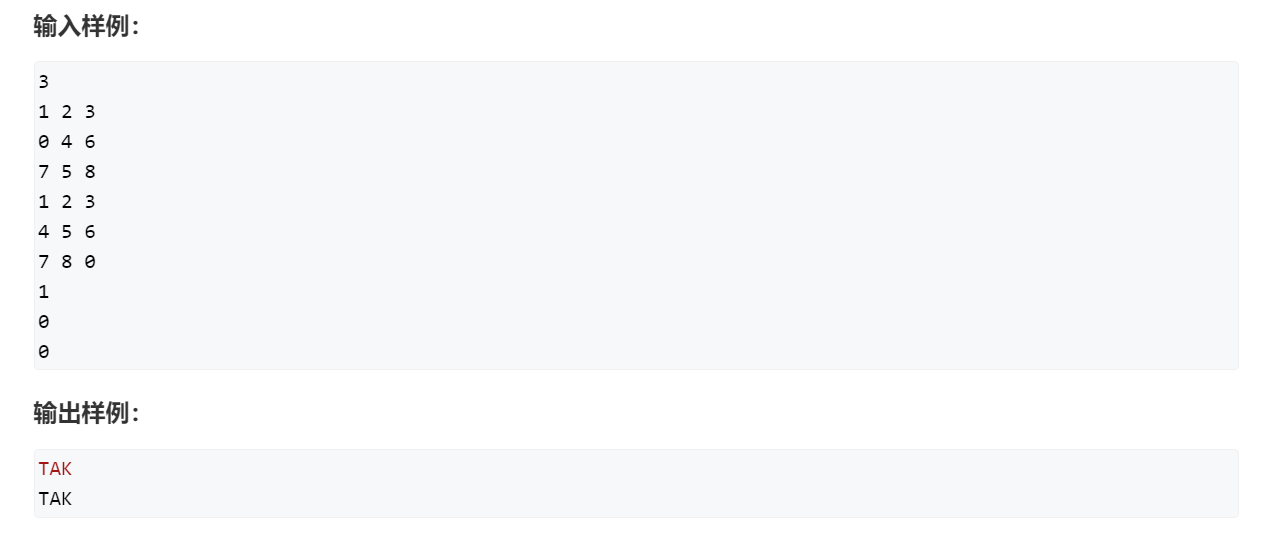
样例代码
#include <bits/stdc++.h>
using namespace std;
const int N=510;
int n,m,a[N*N],b[N*N],c[N*N],i,j,k;
long long cnt;
void merge(int a[],int l,int r)
{
if (r-l<1)
return ;
int mid=(l+r)>>1;
merge(a,l,mid);
merge(a,mid+1,r);
int i=l,j=mid+1;
for (int k=l; k<=r; k++)
{
if (j>r || i<=mid && a[i]<=a[j])
b[k]=a[i++];
else
{
cnt+=mid-i+1;
b[k]=a[j++];
}
}
for (int k=l; k<=r; k++)
a[k]=b[k];
}
signed main()
{
ios::sync_with_stdio(false);
// freopen("stdin.in","r",stdin);
// freopen("stdout.out","w",stdout);
while(cin>>n)
{
int ok=0,x;
for (i=1; i<=n*n; i++)
{
cin>>x;
if (x==0)
ok=1;
else
a[i-ok]=x;
}
ok=0;
for (i=1; i<=n*n; i++)
{
cin>>x;
if (x==0)
ok=1;
else
c[i-ok]=x;
}
cnt=0;
memset(b,0,sizeof(b));
merge(a,1,n*n);
long long ans=cnt;
memset(b,0,sizeof(b));
cnt=0;
merge(c,1,n*n);
if ((ans&1)==(cnt&1))
puts("TAK");
else
puts("NIE");
}
return 0;
}


