N皇后问题、分治法、01背包问题

1.N皇后问题（非递归）

#include<stdio.h>
#include <math.h>
#define N 4
int q[N + 1]; //存储皇后的列号

//检查第j个皇后的位置是否合法
int check(int j) {
    int i;
    for (int i = 1; i < j; i++) {
        if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) {
            //判断是否在同一列和同一斜线上
            return 0;
        }
    }
    return 1;
}

void queen() {
    int i;
    for (i = 1; i <= N; i++) {
        //初始化为0
        q[i] = 0;
    }
    int answer = 0;//方案数
    int j = 1;
    while (j >= 1) {
        //摆放皇后的位置
        q[j] = q[j] + 1;
        //检查位置是否合法
        while (!check(j) && q[j] <= N) {
            //不合法
            q[j] = q[j] + 1;
        }
        if (q[j] <= N) {
            //表示第j个皇后找到了合法的摆放位置
            if (j == N) {
                //找到了一组解
                answer = answer + 1;
                printf("方案%d: ", answer);
                for (i = 1; i <= N; i++) {
                    printf("%d ", q[i]);
                }
                printf("\n");

            }
            else {
                //继续摆放下一个皇后
                j = j + 1;
            }

        }
        else {
            //第j个皇后找不到合法的位置
            q[j] = 0;//还原当前皇后的位置
            j = j - 1;//回到上一个皇后处修改位置
        }
    }
}

int main() {
    queen();
　　return 0;
}

 2，4，1，3

3，1，4，2

2.N皇后问题（递归法）

#include<math.h>
#include<stdio.h>
#define N 4
int answer = 0;
int q[N + 1];

int check(int j) {
    for (int i = 1; i < j; i++) {
        if (q[i] == q[j] || abs(i - j) == abs(q[i] - q[j])) {
            return 0;
        }
    }
    return 1;
}

void queen(int j) {
    int i;
    for (i = 1; i <= N; i++) {
        q[j] = i;
        if (check(j)) {
            if (j == N) {
                //找到一组解
                answer = answer + 1;
                printf("方案%d: ", answer);
                for (int i = 1; i <= N; i++) {
                    printf("%d ", q[i]);
                }
                printf("\n");
            }
            else {
                //摆放下一个皇后
                queen(j + 1);
            }
        }
    }

}
int main() {
    queen(1);
    return 0;
}

3.分治法

#include<stdio.h>
#define MAX 65536

void Merge(int A[], int p, int q, int r) {
    int i, j, k;
    int L[50], R[50];
    int n1 = q - p + 1, n2 = r - q;
    for (i = 0; i < n1; i++) {
        L[i] = A[p + i];
    }
    for (j = 0; j < n2; j++) {
        R[j] = A[q + j + 1];
    }
    L[n1] = MAX;
    R[n2] = MAX;
    i = 0;
    j = 0;
    for (k = p; k < r + 1; k++) {
        if (L[i] < R[j]) {
            A[k] = L[i];
            i++;
        }
        else {
            A[k] = R[j];
            j++;
        }
    }

}
void MergeSort(int A[], int p, int r) {
    int q;
    if (p < r) {
        q = (p + r) / 2;
        MergeSort(A, p, q);
        MergeSort(A, q + 1, r);
        Merge(A, p, q, r);
    }
}
int main() {
    int A[] = { 4,1,3,6,7,5,2,9 };
    MergeSort(A, 0, 7);
    int i;
    for (int i = 0; i < 8; i++) {
        printf("%d ", A[i]);
    }
    return 0;
}

4.动态规划法：0-1背包问题

 

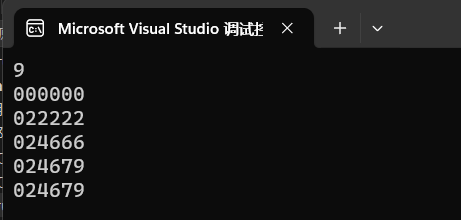
#include<stdio.h>
#include<math.h>
#define N 4        //物品数量
#define W 5        //背包容量

int max(int a, int b) {
    return a > b ? a : b;
}

int main() {
    //下标从1开始
    int v[] = {0,2,4,5,6};        //物品价值数组
    int w[] = {0,1,2,3,4};        //物品重量数组
    int f[N + 1][W + 1] = {};        //子问题解数组
    int i, j;
    for (i = 1; i <= N; i++) {
        for (j = 1; j <= W; j++) {
            //优化
            f[i][j] = f[i - 1][j];//默认不选第i个物品
            if (j >= w[i]) {
                f[i][j] = max(f[i - 1][j], f[i - 1][j - w[i]] + v[i]);
            }

            /*
            if (j >= w[i]) {
                //选第i个物品的条件
                f[i][j] =max(f[i-1][j], f[i - 1][j - w[i]] + v[i]);
            }
            else {
                //
                f[i][j] = f[i - 1][j];
            }*/
        }
    }
    printf("%d\n", f[N][W]);
    for (i = 0; i <= N; i++) {
        for (j = 0; j <= W; j++) {
            printf("%d", f[i][j]);
        }
        printf("\n");
    }
    return 0;
}