一维概率密度与二维概率密度图像表示

首先明白一下概率密度函数与概率质量函数的区别：

 

 总结：概率密度函数是针对连续随机变量而言的；概率质量函数是针对离散型随机变量而言的。

 

（1）一维概率密度：

P(X)是概率密度函数，对P(X)积分就变为概率的值。

 

 

注：在一维概率密度函数中，可以用该函数在二维平面中的面积来表示某个区域的概率大小。

（2）二维概率密度： 

 

 如上，以一个二维均匀分布（在该区域内，取到每个点的概率相等）的概率密度函数为例子：

 

下面画出这个函数在空间的区域图像。

 

 

 

根据概率密度函数的规范性：可知概率密度累积函数的大小为1，也就是说对概率密度函数进行积分，结果为1.

下面图像就是针对二维随机变量的概率密度函数积分的几何意义。

 

 

注：在二维概率密度函数中，可以用该函数在三维空间中的体积来表示某个区域的概率大小。

 再次说明：其实二维概率密度函数进行积分，就是就是进行二重积分，二重积分说白了就是求曲顶柱体的体积（曲顶柱体是空间中的立体图形）

 

 

 ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------

补充说明：

（1）二重积分

 

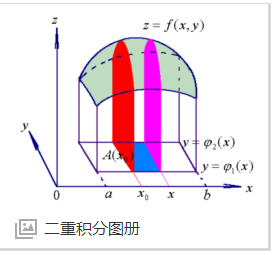
 百度百科的定义：

 

 大白话解释：其实说白了就是，在xoy平面坐标系中，有一个平面区域，这个区域的所有值（x,y）都与一个函数 f(x,y)(设f(x,y)=z)上面的值互相对应。

确定了这个平面区域内的某个值（x,y）,那么就能确定z值的大小。由于在xyz空间直角坐标系中，某一个确定的（x,y）其实有无穷多个，例如（9，9）在空间

中有无数个，这无数个形成了一条直线，然后这条直线在x上积分，就变成面，形成的面在y上积分就变成了曲顶柱体。所以曲顶柱体的体积就是二重积分的值。

形象一点解释：你可以把二重积分看成一盒薯条，薯条盒底面有无数个点，每个点都放着一根薯条，把所有薯条加起来就近似薯条盒这个曲顶柱体的体积。

（2）三重积分

 

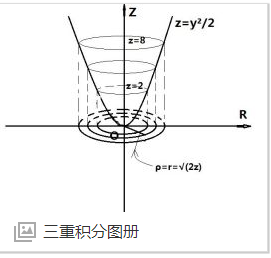
 三重积分的定义：

 

 

解释说明：三重积分说白了就是在空间中有一个区域，这个区域是立体几何图形，然后把这个区域分解成无数个小颗粒，每个小颗粒都有质量，

然后把所有小颗粒在x,y,z三个方向上面积分，就从小颗粒-->变成小细棍-->变成有质量的曲顶柱体。

 

最后总结：初学者很容易搞混二重积分和三重积分，会误以为它们都是求立体几何的体积。

一、两者的实质不同：

1、二重积分的实质：表示曲顶柱体体积。

2、三重积分的实质：表示立体的质量。

 

二、两者的概述不同：

1、二重积分的概述：二重积分是二元函数在空间上的积分，同定积分类似，是某种特定形式的和的极限。本质是求曲顶柱体体积。重积分有着广泛的应用，可以用来计算曲面的面积，平面薄片重心等。平面区域的二重积分可以推广为在高维空间中的（有向）曲面上进行积分，称为曲面积分。

 

2、三重积分的概述：设三元函数f（x,y,z）在区域Ω上具有一阶连续偏导数，将Ω任意分割为n个小区域，每个小区域的直径记为rᵢ（i=1,2,...,n），体积记为Δδᵢ，||T||=max{rᵢ}；

在每个小区域内取点f（ξᵢ，ηᵢ，ζᵢ），作和式Σf（ξᵢ，ηᵢ，ζ）Δδᵢ，若该和式当||T||→0时的极限存在且唯一，则称该极限为函数f（x,y,z）在区域Ω上的三重积分，记为∫∫∫f（x,y,z）dV，其中dV=dxdydz。

 

三、两者的数学意义不同：

1、二重积分的数学意义：在空间直角坐标系中，二重积分是各部分区域上柱体体积的代数和，在xoy平面上方的取正，在xoy平面下方的取负。某些特殊的被积函数f（x，y）的所表示的曲面和D底面所为围的曲顶柱体的体积公式已知，可以用二重积分的几何意义的来计算。

 

2、三重积分的数学意义：如果空间闭区域G被有限个曲面分为有限个子闭区域，则在G上的三重积分等于各部分闭区域上三重积分的和。

二重积分和三重积分并不都是可以用来计算体积的。二重积分可以用来计算体积，而三重积分不可以用来计算体积。