网络流问题

前言

这篇文章的大多数图片来自这个视频。膜拜 & 支持原创。
前置芝士: 链式前向星存图。

网络流问题是图论的一个分支，算法难度并不难，但主要难度在于建图。网络流问题的建图思想在图论问题中还是有很大用处的。

本文讨论网络最大流，网络最小割，网络费用流三大问题，并有例题后附。

网络流问题

什么是流呢？想象一个有防倒流阀门的水管网络，流就是每一个水管中单位时间内通过的水的体积。通常每个水管都有自己的最大流量限制。我们把最大流量换算为边权，把实际通过的流叫做边上的流。为方便表示，用 \(c(u,v),f(u,v)\) 分别表示边 \((u,v)\) 的最大流量以及当前通过的流。

网络流问题在一个有向有权图上（我们下面称作网络流图），图中有一个源点，一般记作 \(s\)，还有一个汇点，一般记作 \(t\)。从源点可以产生一些流量，经过途中的一些边到达汇点，但是每条边经过的流量有限制。\(s\) 节点上有无限的流，\(t\) 节点可以接受无限的流，网络流问题围绕着流的一些性质展开。

在网络流问题中，不论何时，流有如下几个条件应满足：

• 容量限制：\(f(u,v) \le c(u,v)\) 应恒成立。
• 流守恒：\(\sum f(u_i,u)=\sum c(u,v_i)\)，也就是：进入一个节点的流必须等于节点发送出去的流。节点不能将流凭空消失（除了 \(t\)），也不能凭空产生流（除了 \(s\)）。

最大流问题

最大流问题中，我们的目标是：合力安排每条边通过的流量，在流的状态合法的情况下，使进入 \(t\) 的流量最大。
你可能一个想到的是搜索，我们希望找到一条从 \(s\) 到 \(t\) 的路径，使得路径上的 \(f \le c\)，这意味着我们可以安排一条流经过这个路径从 \(s\) 到 \(t\)，答案可以更优。

看起来这种路径很重要，我们给这种路径起名叫增广路。

一种贪心的做法是：每找到一条增广路就安排流量，一直到找不到。 此时的答案？

是不对的，原因在于搜索到边的顺序问题，可能有更好的边能提供更多的流量，但是在搜索时却先把一个较小的流量加载上导致本来可以加载的较大的流量无法被加载，于是程序会得出错误的答案。

这里就不举例了，网上的例子也有很多。

但我们的想法不是完全没用的，这样求解出来的流叫做阻塞流，我们可以使用 DFS 很简单地写出求解阻塞流的代码，注意：这里的 DFS 对其中的变量有详细注释，下文各种算法的 DFS 都和这个差不多，可以仔细看看。

int dfs(int u,int maxf){
	//u 表示点编号，maxf 表示到这个点时还有多少的可用流量给到下一些点 
	vis[u]=1;//避免重读访问标记 
	if(u==t){//找到汇点了 
		return maxf;//直接返回可能的最大流量 
	}
	int ccnt=0;//从这个点引出了多少流量 
	for(int i=_head[u];i!=-1&&ccnt<maxf/*送出去的流量必须小于给到这个点的流量*/;i=edge[i].nxt){
		int v=edge[i].v;//下一个点 
		int w=edge[i].w;//到下一个点的这条管道的边权最大限制 
		if(w&&!vis[v]){//有空间且下一个点还没更新 
			int vreq=dfs(v,min(maxf-ccnt,w));
			/*向下一个点去，这里min(maxf-ccnt,w) 意思是：如果当前还能继续用的流量小于边的流量限制那么就只能用剩下的了
			  问题就出在这：可能前面会有多个较小的w挤占了大量的空余流量导致一个较大的w无法充分的利用导致错误的答案*/ 
			if(!vreq)dis[v]=0;//找不到就把这个点关掉， 
			edge[i].w-=vreq;//把边减去消耗的空间 
			ccnt+=vreq;//已经用的流量要加上 
		}
	}
	return ccnt;//返回用的流量 
}

发现找增广路不会让答案变劣，于是反悔贪心？

关键在这里，我们通过建立反向边达到撤销并重新分配流使得答案不减。这是如何做到的？

给反向边如下的定义：反向边增加一单位的最大流量代表正向边减少一个单位的流量，搜索增广路时可以经过反向边。举例来看：

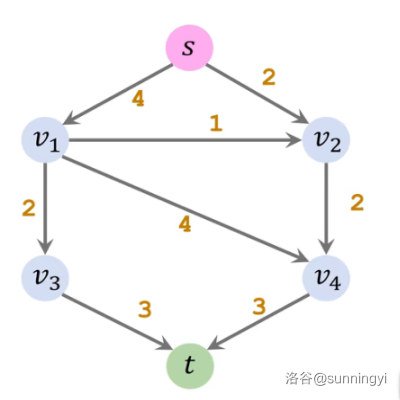
首先我们找到一条阻塞流：

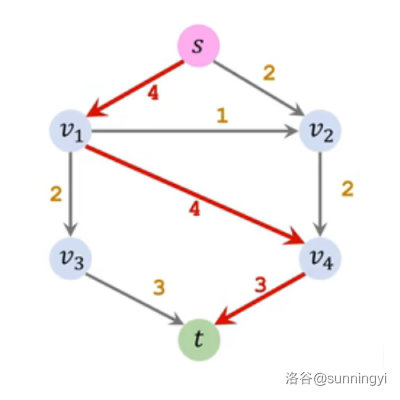
把流量加载上，然后把用到的流量建成反向边：

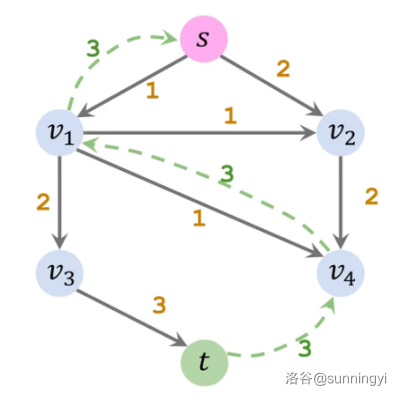
重复这个过程：


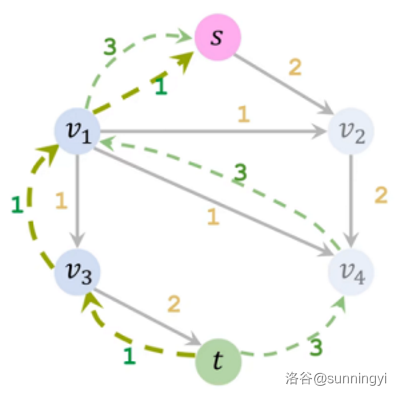
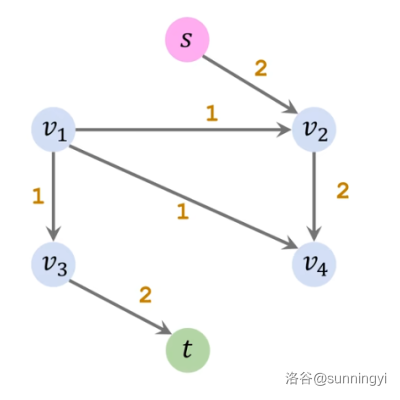
这时已经不可以只通过正向边来到达汇点了，但好在反向边也是可以走的，我们可以找到这样的一条路径：

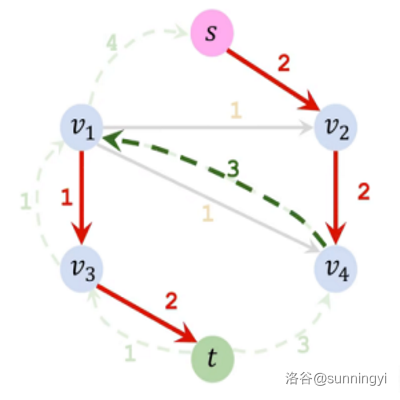
此时我们依然可以向这条路径上加载流量 \(1\)，这样的流量也算在答案中。

解析一下，\(s,v_2,v_4,v_1,v_3\) 这条路径中，经过那条边权为 \(3\) 的反向边，相当于我们已知从 \(v_4\) 点出发，至少有 \(3\) 的流量可以通往 \(t\)。而且我们现在还有能力部分接管这个流。于是，我们尝试把从 \(v_1\) 到 \(v_4\) 的流推回，让这个流借着这一次搜索重新规划路线，至于要退回去多少就要看重新规划的路线能规划出多少了。如果可以成功推回，就相当于帮助一部分流从 \(v_1\) 又找到了一条路径到 \(t\)，此时让这一部分流从这条路径走，我们就可以去接管这部分从 \(v_4\) 开始的流了。

因此，虽然我们是因为帮助 \(v_1\) 到 \(v_4\) 的流重新规划操加载上的 \(1\) 流量，可以直接等价于两次搜索到两条增广路。

为此，我们引入残量网络：可以理解为把用完流量的边移去，把没用完的边的剩余部分流量作为新边权（不算反向边）构建出的新图。这种图的用途后面介绍。

接下来讲解基于建反向边原理的 Ford-Fulkerson 算法。

Ford-Fulkerson 算法

简称 FF 算法。

基于上文的寻找增广路原理，由于需要记录反边所以要用链式前向星存图。使用 DFS 寻找增广路径，维护路径上最小剩余流量，回溯时进行“减少正向边剩余，增加反向边剩余”的操作，若无法找到增广路则算法结束，此时答案即为最大流。

code，不怎么常用，但可以为下面更优化的算法提供模板：
建反边需要使用链式前向星。

const int M=1e6+5;
const int N=1e4+5;
struct{
	int v;
	int w;
	int nxt;
}edge[M*2];
int _head[N];
int e_cnt=-1;
int n,m,cm;
void add(int u,int v,int w){
	e_cnt++;
	edge[e_cnt].v=v;
	edge[e_cnt].w=w;
	edge[e_cnt].nxt=_head[u];
	_head[u]=e_cnt;
} 
int dis[N];
bool vis[N];
int dfs(int u,int maxf){
	vis[u]=1;
	if(u==m+n+1){
		return maxf;
	}
	int ccnt=0;
	for(int i=_head[u];i!=-1&&ccnt<maxf;i=edge[i].nxt){
		int v=edge[i].v;
		int w=edge[i].w;
		if(w&&!vis[v]){
			int vreq=dfs(v,min(maxf-ccnt,w));
			if(!vreq)dis[v]=0;
			edge[i].w-=vreq;
			edge[i^1].w+=vreq;
			ccnt+=vreq;
		}
	}
	return ccnt;
}
int FF(){
	int res=0;
	int flow=0;
	while(flow=dfs(0,1e9)){//不停找阻塞流 
		res+=flow;//加上新流量 
		memset(vis,0,sizeof vis);	
	}
	return res;
}

它快吗

设一个网络流图的最大流值为 \(F\)，边数为 \(M\)，则 FF 算法的最坏时间复杂度为 \(O(MF)\)。

为什么呢，有这样一个卡 FF 算法的经典图：

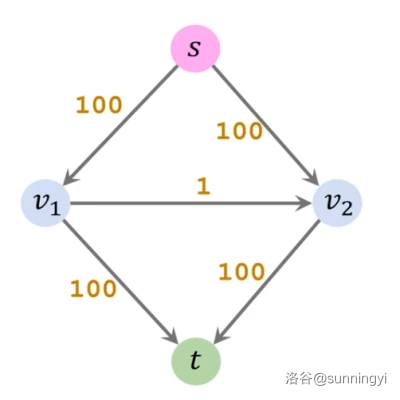
相信你看一眼就知道为什么了。

当然了，我们有办法让他更快。

Edmonds-Karp 算法和时间复杂度

简称 EK 算法。

定义网络流图中每条边对路径长度的贡献为 \(1\)，则我们需要做的就是每次都找那条最短的增广路增广。

在一个边权都为 \(1\) 的有向图中找到最短路的时间复杂度是 \(O(E)\) ，也就是一次 BFS 的时间复杂度。

于是，EK 算法的时间复杂度为 \(O(VE^2)\) 。

简要证明如下，来自这里

首先每次我们找到一条增广路的时候肯定会把它压榨干净, 也就是说至少有一条边在这个过程中被跑满了. 我们把这样的边叫做 关键边. 增广之后, 这些边在残量网络中都会被无视掉. 也就是说这条路径就这么断掉了. 而我们每次都增广最短路, 也就是说我们每次都在破坏最短路. 所以 \(s,t\) 之间的最短路单调递增.

因为增广路必然伴随至少一条关键边出现, 所以我们可以把增广过程的迭代次数上界转化为每条边成为关键边的次数.

因为关键边会从残量网络中消失, 直到反向边上有了流量才会恢复成为关键边的可能性, 而当反向边上有流量时最短路长度一定会增加. 而最短路长度不会超过 \(V\)，所以总迭代次数是 \(O(VE)\) 的。

因为EK算法中残量网络上的最短路是 \(0/1\) 最短路, 直接BFS实现的话时间复杂度是 \(O(E)\) 的, 于是 EK 算法总时间复杂度 \(O(VE^2)\), 证毕.

实现上来说，在每次 DFS 前用一边 BFS 求解出最短路，然后沿着最短路走就可以了。

它够快了吗

还不够，如果是稠密图，时间复杂度可以到 \(O(V^3)\) 甚至 \(O(V^5)\)。

问题在于：EK 算法每次只会增广一条最短路。

BFS 真的每次只会找到一条增广路吗？

考虑如下网络流图：

（png）

BFS 后：

（png）

去掉相同层级间的边连接？

（png）

给这么多增广路增广只需要用一次 DFS 就好了。（吗？

于是，我们得到了一个更优秀的算法：

Dinic 算法

我们将 EK 的 DFS 改为相邻 dep 的节点都增广，就是 DInic 算法。

通过这种改进，DInic 算法的时间复杂度为 \(O(V^2E)\)。

code：

const int N=1e4;
const int M=1e5;
struct e{
	int u;int v;int w;int nxt;
}edge[M*2];
int idx=-1; int n,m,cm; int _head[N];
void add(int u,int v,int w){
	idx++;
	edge[idx].u=u; edge[idx].v=v; edge[idx].w=w;
	edge[idx].nxt=_head[u];
	_head[u]=idx;
	return ;
}
int dis[N]; int cur[N];
int s,t;
bool bfs(){
	memset(dis,0,sizeof dis);
	queue<int> q;q.push(s);
	dis[s]=1;
	cur[s]=_head[s];
	while(q.size()){
		int u=q.front();q.pop();
		for(int i=_head[u];i!=-1;i=edge[i].nxt){
			int v=edge[i].v,w=edge[i].w;
			if(!dis[v]&&w){
				dis[v]=dis[u]+1;
				cur[v]=_head[v];
				if(v==t)return 1;
				q.push(v);
			}
		}
	}
	return 0;	
}
int dfs(int u,int maxf){
	if(u==t)return maxf;
	int ccnt=0;
	for(int i=cur[u];i!=-1&&ccnt<maxf;i=edge[i].nxt){
		int v=edge[i].v,w=edge[i].w;
		cur[u]=i;
		if(dis[u]+1==dis[v]&&w){
			int gos=dfs(v,min(maxf-ccnt,w));
			if(gos==0)dis[v]=0;
			edge[i].w-=gos;edge[i^1].w+=gos;
			ccnt+=gos;
		}
	}
	return ccnt;
}
int dinic(){
	int res=0;
	int flow=0;
	while(bfs())
		while(flow=dfs(0,1e9))
			res+=flow;
	return res;
}

且慢，上面代码中的 cur[] 数组是干什么的？DFS 中 dis[v]=0 又有什么用？

原因在于，如果不加这两个东西，Dinic 的时间复杂度是假的，原因出在 DFS 过程中。

我们都知道，图上的 DFS 需要使用 vis[] 数组标记节点来保证其单次正确的时间复杂度，但是在 Dinic 中，DFS 需要多次经过两个节点，如上图中的例子。

那这两个东西有什么用？先看 dis[v]=0 ：

如果dis[v]=0 ，代表不会有一个点满足 \(\operatorname{dis}(u)+1=\operatorname{dis}(v)\) 了，相当于这个点被我们无视掉了。原因就在判断条件里：在本次 BFS 安排好的 dis 增广顺序中，\(v\) 无法在被安排上任何流量。由于 BFS 会搜出来一个 DAG，意味着不会有反边来让 \(v\) 可以重新通开了，也就是说，\(v\) 什么用都没有了，这时候把它优化掉就可以了。

再看 cur[] 数组：

这种优化称为当前弧优化，我们每次向一条边的方向推流的时候，要么 dis 关系不满足，要么把推过去的流量用完了，要么把这一条边上的剩余流量榨干了。除了第二种情况，第一、三种情况里的这一条边什么用都没有了，于是我们把这条边优化掉，防止再次遍历回到这个点时再因为寻找出边浪费时间。cur[] 数组就是干这个活的。

经过这两个优化，可以证明 Dinic \(O(V^2E)\) 的时间复杂度了。
（怎么证，不道啊（逃

它够快了吧？

在比赛中应该是够了。这里要指出的一点是：Dinic \(O(V^2E)\) 的时间复杂度非常难跑满，在一定范围内，即使 \(V^2E\) 的值远大于计算机的计算极限，Dinic 算法仍可以通过。

另外，在一些性质良好的图上，Dinic 算法的时间复杂度会更优。对于二分图匹配问题，Dinic 算法有 \(O(\sqrt{V}M)\) 的时间复杂度上界。更多细节可以参考OI Wiki 上的介绍。

但是，我们还有跑的更快的算法：

预流推进之 HLPP 算法

预留推进，什么是预流？怎么样推进？

如果你之前没有学过 DFS，BFS 算法的话，看到开头关于最大流问题的描述，你可能第一个想到这种东西：把源点看成水龙头，把粗细不同的管子在竖直方向按照一定的高度顺序排列起来，把下水道（汇点）放在最底下，然后打开水龙头。此时水会因为重力势能自然经过管子向下流淌，此时流进下水道的流不就可以看成最大流了吗？

说得好，奖励你用 Blender 通过物理模拟求解最大流

但是，这种思路是对的，而且就是预流推进算法的基本原理 ：往 \(s\) 里拼了命的灌水，\(t\) 能有多少水流，就是最大流。

当然，肯定不会让你写一个物理引擎的啦，我们形式化的模拟一下这个过程就好了。

为了实现这种算法，我们往图里在加点料。

预留推进思想

在之前的最大流算法中，算法总是在任意时刻维护一个合法的流，这样的流要满足的性质之一是流守恒原则，回顾一下吧：

• 流守恒：\(\sum f(u_i,u)=\sum c(u,v_i)\)，进入一个节点的流必须等于节点发送出去的流。节点不能将流凭空消失（除了 \(t\)），也不能凭空产生流（除了 \(s\)）。

但现在，我们让流可以在一个节点中暂存，即：进入节点的流可以多余节点实际发出的流。相当于在节点外接一个水库，水库里可以存储无限的流。为了与之前的流的定义区别，我们称这种流为预流。预流弱化了流守恒原则，形式化定义一下：对于所有的节点，任意时刻的预流应满足：

\[\sum f(v,u) - \sum f(u,v) \ge 0 \]

我们定义函数 \(e\)：

\[e(u)=\sum f(v,u) - \sum f(u,v) \]

为节点 \(u\) 的超额流，这些流都存在上文类比的水库中去了。如果一个节点有超额流，我们称这个节点溢出（MLE）了。特殊地，源点和汇点被定义为永远不会溢出。

但是，有了水库又怎样？流该去哪里呢？

我们把这些点及其连接的水库分层，相当于我们口胡想象里的高度关系。一个点和它的水库总是在同一层，节点所在的层可以变化，变化由算法控制。

节点的高度决定了流的推送方向：我们只能从高处往低处推送流，虽然低处的节点向高处的点可能也会有流，但是这个高度限制只在推流时被考虑。初始时，我们将源点的高度设置为 \(|V|\) ，即点的数量；汇点的高度设置为 \(0\)；所有其它节点的初始高度也都是 \(0\)，但将随着时间的推移不断增加。

我们模拟的思路是：第一步，从源节点向四周的节点下发尽可能多的流（这里不考虑高度关系），这些流将被存储在这些点的水库中，从这里开始，水流将被向下面的节点推送。

在推送的过程中，我们可能会发现一个点有超额流，但是它邻接的点都比这个点要高，为了消除超额流，必须增加该节点的高度，一些书中（例如《算法导论》）称这个操作为重贴标签。我们将这个点的高度更改为在所有 邻接的 有空闲流量 的边 连接的点 中，高度最小的那一个，这样可以保证节点至少有一个管道可以推送更多的流。

最终，所有可能到达汇点的流都已经到达汇点，为了让这个预流称为一个合法的流，我们需要让所有点满足流守恒，此时就要把所有溢出的节点中的流再次通过增加高度的方式重新送回源点。一旦所有的水库都为空，预流将称为一个合法的流，而且是最大流。

接下来说说实现的细节吧

最高标号预流推进（HLPP）

在上面思想的叙述中，我们并未提到是怎么发现一个有超额流的点的。事实上，如果我们以任意的次序去对这些点进行操作，得到的算法是 \(O(V^2E)\) 的，但是它实际上跑的比 Dinic 慢。

最高标号预留推进让我们每次对一个高度 最高的 且 有超额流的 点进行操作。通过这样的操作顺序，HLPP 的时间复杂度为 \(O(V^2 \sqrt{M})\)。

很厉害吧，但是它依然跑的没有 Dinic 快，原因是维护最高标号要用优先队列，常数大了。

为此，我们还有些优化：

给所有非源汇节点的高度设置为 \(0\) 是最优的吗？当我们从源点向第一阶梯的点推流以后，各点之间需要从 \(0\) 开始左右互博提高高度，当可以向汇点推流时，你大概可以想象到，由于我们推流应满足高度差为 \(1\)，因此图中各点的高度大致是一个阶梯关系。那么我们不妨直接在开始时就让这个图是个阶梯，此时流可以顺流而下，直接从这个高度开始互博，将超额流退回去即可，最大流仍是正确的。

当点升高到一定高度且没有超额流之后，这些点还会对答案做出贡献吗？实际上，如果一个点 \(v\) 再被重贴标签以后，如果它原来的高度已经没有其它点，那么高于它的点一定不能将流量推送到 \(t\) 了。

为啥呢？由于我们推流应满足高度差为 \(1\)，而且我们找到的点又是溢出的点中最高的，这意味着其上的点全都不溢出，而有一层已经没有点了，由于源汇点的高度不会变，此时相当于楼层之间的梯子被撤掉了，即使上面的点还有流量，也不能下放到 \(t\) 了。这是什么原理？我们从之后可能被重贴标签的点到这里可能产生的情况分别考虑：

• 之后的点上跳到 \(u\) 原来那一层，由于上面的点没有超额流，即使有了梯子，也不会再下放了。
• 之后的点上跳到比 \(u\) 原来还高的一层，由于通过这一层的梯子依然没有就位，不可能下放了。

那么，有没有可能 之后的点上跳到 \(u\) 原来那一层，之后的点再上跳到比 \(u\) 原来还高的一层，形成一个组合技呢？虽然有可能，但是这与 \(u\) 更新时的那些比它高的点就没关系了。

情况可能有点多，上个图可能更好理解：

（上跳到 \(u\) 原来那一层，由于上面的点没有超额流，不会再下放了,png）

（上跳到 \(u\) 原来还高的一层，由于通过这一层的梯子没了，不可能下放了,png）

于是，我们可以大胆给这些点的高度设置成比源点的高度多 \(1\)，无需一点点提高高度 了。

写了这么多，看看代码吧：

Show me the code

int n,m,s,t;
const int N=1e5+5;
struct e{
  int v;
  ll w;
  int nxt;
};
int head[N];
ll extra[N];
ll gap[N*2+114];
ll h[N];
e edge[N*50];
int cnt=-1;
bool inq[N];
struct work{
  ll u;
  ll h;
  bool operator<(const work &x) const{
    return x.h>h;
  }
};
void add(int u,int v,ll w){
  cnt++;
  edge[cnt].v=v;
  edge[cnt].w=w;
  edge[cnt].nxt=head[u];
  head[u]=cnt;
  return ;
}
priority_queue<work> q;
bool preflow(){
  queue<int> qi;
  qi.push(t);
  memset(h,0x3f,sizeof h);
  h[t]=0;
  while(qi.size()){
    int u=qi.front();
    qi.pop();
    for(int i=head[u];i!=-1;i=edge[i].nxt){
      int v=edge[i].v;
      if(   edge[i^1].w   &&h[v]>h[u]+1){
        h[v]=h[u]+1;
        qi.push(v);
      }
    }
  }
  if(h[s]==0x3f3f3f3f){
    return false;
  }
  h[s]=n;
  for(int i=1;i<=n;i++){
    if(h[i]<0x3f3f3f3f)gap[h[i]]++;
  }
  for(int i=head[s];i!=-1;i=edge[i].nxt){
    ll w=edge[i].w;
    int v=edge[i].v;
    edge[i].w-=w;
    edge[i^1].w+=w;
    extra[v]+=w;
    if(v!=s&&v!=t&&!inq[v]){
      inq[v]=1;
      q.push(work{v,h[v]});
    }
  }
  return true;
}
void pushflow(int u){
  for(int i=head[u];i!=-1;i=edge[i].nxt){
    int v=edge[i].v;
    ll w=edge[i].w;
    if(w&&h[v]+1==h[u]){
      ll gos=min(w,extra[u]);
      edge[i].w-=gos;
      edge[i^1].w+=gos;
      extra[u]-=gos;
      extra[v]+=gos;
      if(v!=s&&v!=t&&!inq[v]){
        q.push(work{v,h[v]});
        inq[v]=1;
      }
      if(extra[u]==0){
        return;
      }
    }
  }
}
void relabel(int u){
  int minh=0x3f3f3f3f;
  for(int i=head[u];i!=-1;i=edge[i].nxt){
    int v=edge[i].v;
    ll w=edge[i].w;
    if(w){
      minh=min(minh,h[v]);
    }
  }
  h[u]=minh+1;
  return ;
}
ll hlpp(){
  if(!preflow()){
    return 0;
  }  
  while(q.size()){
    int u=q.top().u;
    int hi=q.top().h;
    q.pop();
    inq[u]=0;
    pushflow(u);
    if(extra[u]){
      gap[h[u]]--;
      if(gap[h[u]]==0){
        for(int i=1;i<=n;i++){
          if(h[i]>h[u]&&i!=s&i!=t&&h[i]<n+1){
            h[i]=n+1;
          }
        }
      }
      relabel(u);
      gap[h[u]]++;
      q.push(work{u,h[u]});
      inq[u]=1;
    }
  }
  return extra[t];
}
signed main(){
  
  cin>>n>>m>>s>>t;
  memset(head,-1,sizeof head);
  for(int i=1;i<=m;i++){
    int u,v;
    ll w;
    u=rd;
    v=rd;
    w=rd;
    add(u,v,w);
    add(v,u,0);
  }
  cout<<hlpp();
  
  return 0;
}

最小割问题

一个图的割是指：把图的点集合划分成两个子集，其中 \(S,T\) 点分属于不同的集合。割有权值，权值为所有两端的点不在同一个集合里的边的权值（流量）之和。你可以理解为你割断了这些边才把图分成了这样两个部分。

所有割中权值最小的那个称为图的最小割。

我们有个很重要的定理：最大流最小割定理：

任意一张网络流图的最大流和最小割在大小上是相等的。

于是我们可以有许多新的建图方法，把问题转化为决策断掉其中的一些边，这一过程通常涉及正难则反的过程，当然我们可以给边的权值设为无限大代表我们不能断掉这条边。下面来几个题看看吧