ACAM （AC 自动机）

前言

关于自动 AC 机。

名字听起来很高级，实际上是个大杂烩。

前置知识：KMP 算法，Trie 树。

rearranged on 2025 06 05, done!

1. 是什么

AC 是两个人名的缩写，分别是 Alfred V. Aho 和 Margaret J. Corasick.。膜拜Orz

至于 “自动机”，并非单词 Automation，而是 Automaton。

一般简写 AC 自动机为 ACAM。

我们学过的 KMP 算法是在若干个主串里匹配快速匹配一个模式串。但在 ACAM 中，我们要做的是在一个主串里快速匹配若干个模式串。

两种算法的大体思路是相同的：当某一处失配时，通过跳转到一个特定的位置而非从头开始匹配来节省时间。但是 KMP 算法将跳转到的位置在一个字符串中，而 ACAM 跳转到的位置在一棵 Trie 中。

而且，ACAM 不直接使用 next 数组进行跳转，而是利用 next 数组跳转的位置，在匹配时尽可能多的跳转到表示不同模式串的树链上并记录尽可能多的答案。

在 ACAM 中，与 KMP 一样，把存储 “失配时，通过跳转到一个特定的位置” 的数组叫做 fail 指针，下面的代码实现中把它表示为 fil 数组。

虽然由线性数据结构变成了树形数据结构，但是好像更好理解了？

先来看看 ACAM 的 fail 指针表示什么。放张图：

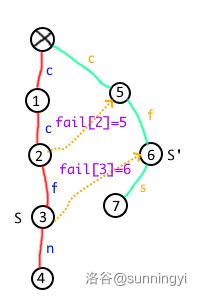
对于节点 \(u\)，设从根节点到 \(u\) 组成的字符串为 \(S\)，从根节点到 fil[u] 组成的字符串为 \(S'\)，如上图所示。

那么 \(S'\) 一定是 \(S\) 的后缀子串，且一定是 \(S\) 的后缀子串中，能在 Trie 树中找到的，从根节点开始的字符串中最长的。

这里与 KMP 算法不同的是，KMP 算法的 next 指针指向自己的存在的最长 Border 的位置，而 ACAM 指向的不止是自己，还可能是其他模式串的后缀子串。

2. 怎么建

首先我们将给定的模式串按从左到右的顺序放到一棵 Trie 中，这一步很简单。

接下来是 ACAM 的核心，求解 fail 数组的过程。

首先，由于 Trie 是一棵树，而 fail 数组需要用父亲节点的 fail 更新而来，因此我们使用 BFS，从根节点向下搜索。这一过程可确保比要求解 fail 的节点深度浅的所有点的 fail 已经被求出。

接下来我们假设要求解 u 节点对应的所有 son[u][i]，即所有儿子节点的 fail。我们遍历所有 son[u][i]，此时分两种情况：

若 son[u][i] 不为零，即可以通过一条代表 i 的边到达一个点，此时我们把它的 fail 的情况放到与主串匹配时来看会更好理解。放张图：

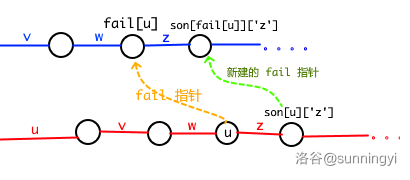
由于 fil[u] 代表的 u 的后缀子串是最长的，因此其用 z 边连接的儿子 son[fil[u]]['z']，也一定是代表 son[u]['z'] 的最长后缀子串。

因此 son[fil[u]]['z'] 满足我们对son[u]['z'] 的 fail 节点的定义，所以：
fil[son[u]['z']]=son[fil[u]]['z']。

进一步，我们可以推广到所有代表不同类型字符的边，因此可以写出如下代码：

for(int i=0;i<26;i++){
    int p=son[u][i];
	  if(p){//son[u][i] 不为零时：
        fil[p]=son[fil[u]][i];
	      q.push(p);//把这个点也放入 BFS 队列中
    }
    ...
}  

你可能有疑问：这个 son[fil[u]][i] 一定存在吗？

如果我们不对 Trie 树进行修改，当然是不一定存在的，但这里我们通过一点小手段让他变为一定存在。

提一嘴，你可能还有一种暴力的思路是去不断的尝试找 son[fil[fil[u]]][i]，但是这样的时间复杂度无法保证。

解决这个问题的方法在 son[u][i] 的值是 \(0\) 的情况里：

为什么跑到 son[u][i] 的值是 \(0\) 的情况了？先别急。

对于 son[u][i] 为零的情况，也就是没有 \(i\) 这条边和其连接的点，我们直接改变 Trie 树的结构，将它赋值给 son[fil[u]][i]。

似乎是一个很奇怪的操作，来看看有什么用：

ACAM 里 fail 的作用是跳最长后缀。

但是这里，这一条树边的作用也是跳最长后缀。

既然 ACAM 是基于跳最长后缀的，那凭什么只让 fail 可以跳最长后缀呢？

等我找找有没有图可以贺。。。

好吧没有，那我自己画。

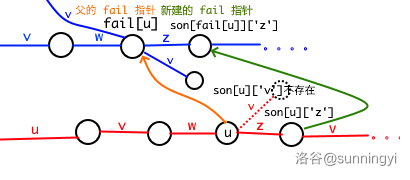
上图中，假设当前 BFS 找到了点 \(u\)，但是 son[u]['v'] 不存在，但是此时 son[fil[u]]['v'] 一定存在。这个存在有两种含义，一个是 Trie 树上本来就有，一个是因为我们已经处理完了 fil[u]，一定给它的各个不存在的 son[fil[u]][i] 了一个别人的 son。

别忘了我们在 BFS 过程中：

我们使用 BFS，从根节点向下搜索。这一过程可确保比要求解 fail 的节点深度小的所有点的 fail 已经被求出。

fail 指向的点的深度一定是比当前点要小的，原因是后缀子串长不能大于原串。所以我们一定已经处理完了 fil[u]。

此时我们在上图中进行 son[u][i]=son[fil[u]][i] 操作，两条红的有向边对应上面的两种情况。

假设你的匹配过程到了 \(u\)，那么你走此时赋值的 son[u]['v'] 到了 son[fil]['v']，就可以等价于你走 fil[son[u]['v']] 到 son[fil]['v'] 了，因为这里原本不存在 son[u]['v']，因此走这条边必然失配，是一定要走这个 fail 的。

你会发现这个东西很聪明在于它压缩了我们上文的暴力想法中的不断跳转 fail 的过程，直接一步到位了。

通过这样的构造方式，我们保证了对于任意的 \(u,i\)，所有 son[u][i] 都存在且是合理的存在，构建 ACAM 的时间复杂度及正确性就有保证了。

这样，我们改变后的 Trie 树变成了一个有向图，我们称这个东西叫 Trie 图。

以下是构造 ACAM 的完整代码，我们把它封装在一个函数中。

void b(){
  queue<int> q;
  for(int i=0;i<26;i++)if(son[0][i])q.push(son[0][i]);
  while(q.size()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(son[u][i]){
        fil[son[u][i]]=son[fil[u]][i];
        q.push(son[u][i]);
      }
      else son[u][i]=son[fil[u]][i];
    }
  }
  return ;
}

完结撒hu。。。欸还没说怎么在 ACAM 上查呢。

当然查找是比建树要简单了啦。

3. 怎么用

首先有结论就是如果我们只走 Trie 树边是会让根节点到我们已经到达的节点的深度最大的，因为我们走树边会让深度加或减（由于我们改变了树的结构），但是走 fail 一定会让我们深度减。

那么，由于 fail 总是在维护最长前缀，这意味着：深度越深，我们跳 fail 的机会越多，能够匹配的机会也就越多，因此我们肯定要贪心的让深度越深越好。

于是，我们枚举主串（这个定义同 KMP 中的）的每个字符，每次只走树边的移动 Trie 上的一个指针 \(u\)，对于每个 \(u\)，不停的跳 fil[u] 知道回到根节点，记录过程中到达的点的出现权值（也就是我们在构建 Trie 的时候给每个字符串终点放的那个 \(1\)），求和即为主串中各模式串的出现次数。

下面是在 ACAM 上查询的代码：

void q(string s){
  int u=0;
  for(int i=0;i<s.size();i++){
    u=son[u][s[i]-'a'];
    for(int j=u;j;j=fil[j]){ans[endp[j]]++;}
    // endp -> endposition -> Trie 树上 p 编号点的出现权值
  }
  return ;
}

完结撒hu。。。。额还没完，你不觉得这东西的时间复杂度有问题吗？

4. 重要的优化

我给你一堆像这样的模式串：

a
aa
aaa
aaaa
aaaaa
aaaaaa
...

再给你一个主串：

aaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaa...

手摸或者感性理解一下你会发现，对于每个位置，跳 fail 的次数是 \(O(n)\) 的。

于是这种查询方式就爆掉了。。。

我们还是转化成算贡献，这里有一个关于 fail 指针构成的很好的性质：

一个 AC 自动机中，如果只保留 fail 边，那么剩余的图一定是一棵树。若 fail 指针严格指向深度浅的点，那么这个数是一个内向树。

于是我们考虑把这个 fail 树拎出来，那么显然所有 ACAM 上的点都应该在这个树上的。

我们首先枚举主串并跟踪 \(u\)，但是不去跳 fail，新开个数组记录我们要在各个点开始跳 fail 的次数，有如下代码：

void q(string s){
  int u=0;
  for(int i=0;i<s.size();i++){
    u=son[u][s[i]-'a'];
    ap[u]++;// 记录各个点开始跳 fail 的次数
  }
  return ;
}

接下来，我们对这个 fail 组成的内向树跑一边拓扑排序，在排序过程中累加 ap 数组。如此这般就可以计算出所有点要被 fail 指针跳到的次数，这个应该容易理解吧。

于是，我们知道了每个点被跳的次数，乘上各点的出现权值，就是各字符串的出现次数了！

现在，关于对 ACAM 最基本的原理的理解，终于可以说完结撒花了！！！

以上被称为 ACAM 的拓扑排序优化，事实上，进行 DFS 也是可以的，因为是棵 fail 树。

当然，如果我们只需要 ACAM 的 fail 树，就不用拓扑优化了，比如那些在 ACAM fail 树上 DP 的题。

先不说那些阴间东西，现在你可以爽爽连切下面三个题！

P5357 【模板】AC 自动机

顺便给出上述优化的模板代码：

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=2e5+5;
int son[N][30],cnt[N];
int fil[N],ap[N],endp[N],apid[N],ans[N];
int id=0,tap=0;
void ins(string s,int &sid){
  int p=0;
  for(int i=0;i<s.size();i++){
    if(!son[p][s[i]-'a'])son[p][s[i]-'a']=++id;
    p=son[p][s[i]-'a'];
  }
  if(endp[p]==0)endp[p]=++tap;
  sid=endp[p];

  return void();
}
int inner[N];
void b(){
  queue<int> q;
  for(int i=0;i<26;i++)if(son[0][i])q.push(son[0][i]);
  while(q.size()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(son[u][i]){
        fil[son[u][i]]=son[fil[u]][i];
        inner[son[fil[u]][i]]++;
        q.push(son[u][i]);
      }
      else son[u][i]=son[fil[u]][i];
    }
  }
}
void q(string s){
  int u=0;
  for(int i=0;i<s.size();i++){
    u=son[u][s[i]-'a'];
    ap[u]++;
  }
  return ;
}
void t(){
  queue<int> q;
  for(int i=0;i<=id;i++)if(!inner[i])q.push(i);
  while(q.size()){
    int u=q.front();q.pop();
    ans[endp[u]]=ap[u];
    int v=fil[u];
    ap[v]+=ap[u];
    inner[v]--;
    if(inner[v]==0)q.push(v);
  }
  return ;
}
int main(){
  
  int n;cin>>n;
  for(int i=1;i<=n;i++){
    string t;cin>>t;
    ins(t,apid[i]);
  }
  string s;cin>>s;
  b();  q(s);  t();
  for(int i=1;i<=n;i++)cout<<ans[apid[i]]<<'\n';
  
  return 0;
}

P3808 AC 自动机（简单版）

code

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e6+5;
int son[N][30],cnt[N];
int fil[N],ap[N],endp[N],apid[N],ans[N];
int id=0,tap=0;
void ins(string s,int &sid){
  int p=0;
  for(int i=0;i<s.size();i++){
    if(!son[p][s[i]-'a'])son[p][s[i]-'a']=++id;
    p=son[p][s[i]-'a'];
  }
  if(endp[p]==0)endp[p]=++tap;
  sid=endp[p];

  return void();
}
int inner[N];
void b(){
  queue<int> q;
  for(int i=0;i<26;i++)if(son[0][i])q.push(son[0][i]);
  while(q.size()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(son[u][i]){
        fil[son[u][i]]=son[fil[u]][i];
        inner[son[fil[u]][i]]++;
        q.push(son[u][i]);
      }
      else son[u][i]=son[fil[u]][i];
    }
  }
}
void q(string s){
  int u=0;
  for(int i=0;i<s.size();i++){
    u=son[u][s[i]-'a'];
    ap[u]++;
  }
  return ;
}
void t(){
  queue<int> q;
  for(int i=0;i<=id;i++)if(!inner[i])q.push(i);
  while(q.size()){
    int u=q.front();q.pop();
    ans[endp[u]]=ap[u];
    int v=fil[u];
    ap[v]+=ap[u];
    inner[v]--;
    if(inner[v]==0)q.push(v);
  }
  return ;
}
int main(){
  
  int n;cin>>n;
  for(int i=1;i<=n;i++){
    string t;cin>>t;
    ins(t,apid[i]);
  }
  string s;cin>>s;
  b();
  q(s);
  t();
  int identity=0;
  for(int i=1;i<=n;i++)identity+=ans[apid[i]]==0?0:1;
  cout<<identity;
  
  return 0;
}

P3796 AC 自动机（简单版 II）

有多测哦！

code

Show me the code

#define psb push_back
#define mkp make_pair
#define rep(i,a,b) for( int i=(a); i<=(b); ++i)
#define per(i,a,b) for( int i=(a); i>=(b); --i)
#define rd read()
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll read(){
  ll x=0,f=1;
  char c=getchar();
  while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
  while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
  return x*f;
}
const int N=1e6+5;
const int MAXN=50000;
int son[MAXN][30],cnt[MAXN];
int fil[MAXN],ap[MAXN],endp[MAXN],apid[MAXN],ans[MAXN];
int id=0,tap=0;
void ins(string s,int &sid){
  int p=0;
  for(int i=0;i<s.size();i++){
    if(!son[p][s[i]-'a'])son[p][s[i]-'a']=++id;
    p=son[p][s[i]-'a'];
  }
  if(endp[p]==0)endp[p]=++tap;
  sid=endp[p];

  return void();
}
int inner[MAXN];
void b(){
  queue<int> q;
  for(int i=0;i<26;i++)if(son[0][i])q.push(son[0][i]);
  while(q.size()){
    int u=q.front();q.pop();
    for(int i=0;i<26;i++){
      if(son[u][i]){
        fil[son[u][i]]=son[fil[u]][i];
        inner[son[fil[u]][i]]++;
        q.push(son[u][i]);
      }
      else son[u][i]=son[fil[u]][i];
    }
  }
}
void q(string s){
  int u=0;
  for(int i=0;i<s.size();i++){
    u=son[u][s[i]-'a'];
    ap[u]++;
  }
  return ;
}
void t(){
  queue<int> q;
  for(int i=0;i<=id;i++)if(!inner[i])q.push(i);
  while(q.size()){
    int u=q.front();q.pop();
    ans[endp[u]]=ap[u];
    int v=fil[u];
    ap[v]+=ap[u];
    inner[v]--;
    if(inner[v]==0)q.push(v);
  }
  return ;
}
string pat[N];
int main(){
  
  while(1){
    int n;cin>>n;
    if(n==0)return 0;
    memset(son,0,sizeof son);memset(cnt,0,sizeof cnt);
    memset(fil,0,sizeof fil);memset(ap,0,sizeof ap);memset(endp,0,sizeof endp);
    memset(apid,0,sizeof apid);memset(ans,0,sizeof ans);memset(inner,0,sizeof inner);
    id=0,tap=0;
    
  for(int i=1;i<=n;i++){
    string t;cin>>t;
    pat[i]=t;
    ins(t,apid[i]);
  }
  string s;cin>>s;
  b();
  q(s);
  t();
  vector<string> ichiroyamaguchi;
  int dxj=0;
  for(int i=1;i<=n;i++){
    if(ans[apid[i]]>dxj){
      dxj=ans[apid[i]];
      ichiroyamaguchi.clear();
      ichiroyamaguchi.push_back(pat[i]);
    }
    else if(ans[apid[i]]==dxj){
      ichiroyamaguchi.push_back(pat[i]);
    }
  }
  cout<<dxj<<'\n';
  for(string v:ichiroyamaguchi)cout<<v<<'\n';
  }
  
  
  return 0;
}

5. ACAM 好题选讲

等我多做点题在写了。