ST 表

前言

各有所长。

1. 原理

ST 表用来解决静态的区间重叠问题（RMQ）问题。如果想要解决动态区间的问题，请使用线段树。
ST 表使用倍增思想，预处理的时间复杂度为 \(O(n\log n)\)。
对比线段树，ST 表的常数更小，更好写，且单次查询的时间复杂度为 \(O(1)\)。

2. 实现

以下以实现查询区间最大值为例。
首先定义一个数组 \(f_{i,j}\) 表示从 \(i\) 往后包括 \(i\) 节点 \(2^j\) 长度区间的最大值。
那么当 \(j\) 等于 \(0\) 时其最大值就是数组本身的值。
之后我们使用倍增法求解，仿照倍增法求解lca的过程，可以轻松写出这个数组的转移方程。如下图:

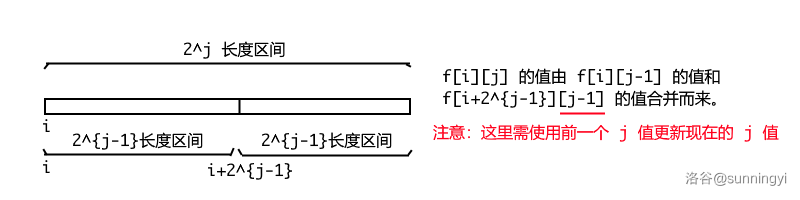
那么，这里第二个区间的起点下标 \(i+2^{j-1}\) 是怎么推导出来的？
我们不妨设第一个区间的结尾处坐标为 \(x\)，则显然第二个区间的起始坐标就是 \(x+1\)。
因为两个区间的长度都是 \(2^{j-1}\) ，因此我们可以得出：

\[x-i+1=2^{j-1} \]

进行简单的移项：

\[x=i+2^{j-1}-1 \]

于是：

\[x+1=i+2^{j-1} \]

考场上如果忘记也可以自己手推。
还要注意，由于我们要用 \(j-1\) 来更新下一个 \(j\)，因此初始化时要先枚举 \(j\)，在内层枚举 \(i\)。
可以写出代码：

// lgr 为倍增法系数，一般是 log n，取 31 足够
for(int i=1;i<=n;i++){
	a[i]=rd;
	f[i][0]=a[i];//每一个 1 长度区间的值都是自己
}
//预处理2的n次方，也可以用位运算，作者懒
p[0]=1;
for(int i=1;i<=lgr;i++){
	p[i]=p[i-1]*2;
}
for(int j=1;j<lgr;j++){
    //            |
    //            V 在这里，要保证 i 向后 2^j 个元素区间的结尾下标不大于 n
	for(int i=1;i+p[j]-1<=n;i++){
		f[i][j]=max(f[i][j-1],f[i+p[j-1]][j-1]);//转移方程
	}
}

很明显这样的预处理是 \(O(n\log n)\) 的。
那么如何查询呢?
假设要查询区间 \(l\) 到 \(r\) 的最大值。
我们来看下图：

为了保证程序的正确性，我们自然希望两个区间重合的越多越好。
这时我们预处理的 \(f\) 数组派上了用场，我们让这个一定长的区间长度为 \(2^{\log r-l+1}\)。
这样我们只需要输出：

max(f[l][log[r-l+1]],f[r-p[log[r-l+1]]+1][s])

问题又来了，函数中第二个 \(f\) 数组的起始下标是如何得出的？
我们设区间起点下标为 \(x\)，则：

\[r-x+1=2^{\log r-l+1} \]

移项：

\[\begin{aligned} -x&=2^{\log r-l+1}-1-r\\ x&=r-2^{\log r-l+1}+1 \end{aligned}\]

对于 \(\log\) 的计算（以下所说的 \(\log\) 皆是以 \(2\) 为底数），我们不采用 <cmath> 中自带的 log() 函数，因为我们只需要任意 \(\log n\) 的整数值。
高中数学告诉我们，\(\log\) 有这样的性质：

\[\log (n\times m)=\log n+\log m \]

于是对于一个数 \(n\)：

\[\log n=\log \left(2\times \frac{n}{2}\right)=\log 2+\log \frac{n}{2} \]

由于 \(\log 2=1\)，于是有这样的递推公式：

\[\log n=1+\log \frac{n}{2} \]

于是我们可以在 \(O(n)\) 的时间复杂度内处理任意 \(n\) 的对数了！
ST 表解决静态区间最大值的完整代码如下：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
#define rd read()
ll read(){
	ll x=0,f=1;
	char c=getchar();
	while(c>'9'||c<'0'){if(c=='-') f=-1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c^48);c=getchar();}
	return x*f;
}
const int N=1e5+5;
const int lgr=31;// lgr 为倍增法系数，一般是 log n，取 31 足够
ll logg[N];
ll f[N][25];
ll a[N];
ll p[30];
int main(){
	
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		a[i]=rd;
		f[i][0]=a[i];//每一个 1 长度区间的值都是自己
	}
	//预处理2的n次方，也可以用位运算，作者懒
	p[0]=1;
	for(int i=1;i<=lgr;i++){
		p[i]=p[i-1]*2;
	}
	for(int j=1;j<lgr;j++){
 	   //            |
 	   //            V 在这里，要保证 i 向后 2^j 个元素区间的结尾下标不大于 n
		for(int i=1;i+p[j]-1<=n;i++){
			f[i][j]=max(f[i][j-1],f[i+p[j-1]][j-1]);//转移方程
		}
	}
	logg[1]=0;//log 1 的值是 0 
	logg[2]=1;//log 2 的值是 1 
	for(int i=3;i<=n;i++){
		logg[i]=logg[i/2]+1;//递推求解 log n 
	}
	for(int i=1;i<=m;i++){
		int l=rd,r=rd;
		int s=logg[r-l+1];//区间长度的 log 
		cout<<max(f[l][s],f[r-p[s]+1][s])<<'\n';//两区间的最大值就是答案 
	}
	
	return 0;
}

3. 例题：

洛谷 P3865 【模板】ST 表
洛谷搬运 P2880 [USACO07JAN] Balanced Lineup G
洛谷 P1816 忠诚
洛谷 P2251 质量检测

迁移自洛谷