组合数与组合计数

前言

Lucas 好抽象。

1. 定义

从 \(n\) 个不同元素中，任取 \(m \leq n\) 个元素组成一个集合，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的一个组合；
从 \(n\) 个不同元素中取出 \(m \leq n\) 个元素的所有组合的个数，叫做从 \(n\) 个不同元素中取出 \(m\) 个元素的组合数，用符号
\(\dbinom{n}{m}\) \dbinom{n}{m} 来表示，读作「\(n\) 选 \(m\)」。
（转载自OI Wiki）

一些时候写作 \(C_n^m\)，公式中常常使用（好像也不常使用了），博客中使用第一种记法。
注意与排列数的区分，一个有序，一个无序。

2. 性质，公式，定理

• 性质 2.1： 特殊的，当 \(\dbinom{n}{m}\) 中 \(m>n\) 时，\(\dbinom{n}{m}=0\)。

• 公式 2.2： 一般地，\(\dbinom{n}{m}=\dfrac{A_n^m}{m!}=\dfrac{n!}{m!(n-m)!}\)，其中 \(A_n^m\) 为 \(n,m\) 的排列数，\(!\) 表示阶乘。

• 公式 2.3： \(\dbinom{n}{m}=\dbinom{n}{n-m}\)。
  很容易证明，考虑这两个数的阶乘式：
  \(\dbinom{n}{m}=\dfrac{n!}{m!(n-m)!}\)。
  \(\dbinom{n}{n-m}=\dfrac{n!}{(n-m)!\left[n-(n-m)\right]!}\)。
  简单计算一下就会发现它们是相等的。

• 公式 2.4： \(\dbinom{n}{m}=\dfrac{n}{m}\times\dbinom{n-1}{m-1}\)
  依然考虑这两个数的阶乘式：
  \(\dbinom{n}{m}=\dfrac{n!}{m!(n-m)!}\)。
  \(\dfrac{n}{m}\dbinom{n-1}{m-1}=\dfrac{n(n-1)!}{m(m-1)!\left[(n-1)-(m-1)\right]!}\)
  对于一个非负整数的阶乘 \(x!\)，显然有 \(x!=(x-1)!\times x\)。
  故 \(n(n-1)!=n!\)，\(m(m-1)!=m!\)。
  对于式子 \(n-m\)，因为 \(n,m\) 同时减小 \(1\)，所以前后相等。
  因此这两个组合数也是相等的。

• 公式 2.5： \(\dbinom{n}{m}=\dbinom{n-1}{m}+\dbinom{n-1}{m-1}\)
  简单的证明：考虑有 \(n\) 个苹果，其中有一个绿苹果，其他都是红苹果，要在里面选任意 \(m\) 个苹果，即有 \(\dbinom{n}{m}\) 种方法选。
  考虑选出来的苹果颜色情况，可以分为包含绿苹果的情况和不包含绿苹果的情况，显然这两种情况的和就是 \(\dbinom{n}{m}\)。
  对于包含绿苹果的情况，我们把绿苹果单独拿出来，其等价于在总的 \(n-1\) 个苹果中选择 \(m-1\) 个苹果的方法数，即 \(\dbinom{n-1}{m-1}\)。
  对于不包含绿苹果的情况，我们把绿苹果从整个苹果堆中拿出来，其等价于在总的 \(n-1\) 个红苹果中选择 \(m\) 个红苹果的方法数，即 \(\dbinom{n-1}{m}\)。
  因此原式得证。
  同时使用这个公式也可以通过数学归纳法证明组合数一定是整数。

• 公式 2.6： 如果 \(p\) 为质数，则 \(p|\dbinom{p}{k}\)
  证明：由公式 2.4 可得：

  \[\dbinom{p}{k}=\frac{p}{k}\times \dbinom{p-1}{k-1} \]

  等式两边同时乘以 \(k\)：

  \[k\dbinom{p}{k}=p\dbinom{p-1}{k-1} \]

  容易得到：

  \[p|p\dbinom{p-1}{k-1} \]

  代入：

  \[p|k\dbinom{p}{k} \]

  引入引理：

  对于质数 \(p\)，若 \(p|a_1a_2\cdots a_n\)，则 \(p|a_1\)，\(p|a_2\) …… \(p|a_n\) 中至少一个成立。
  容易证明：因为 \(p|a_1a_2\cdots a_n\) 且 \(p\) 为质数，所以 \(a_1a_2\cdots a_n\) 必有 \(p\) 这一质因子。
  也就是说 \(a_1\sim a_n\) 中必有一个及以上的数含有 \(p\) 这一质因子。
  因此必有一个及以上的 \(a_i\) 可以被 \(p\) 整除，证毕。

  回到原式中，因为 \(p\) 为质数，所以 \(p,k\) 互质，由引理可得 \(p|\dbinom{p}{k}\)，原式得证。

定理 2.7： 二项式定理

小学二年级我们就知道，\(\left(a+b\right)^2=a^2+2ab+b^2\)。
那么 \(\left(a+b\right)^n\ \ \ (n\in\mathbb{Z}^*)\) 又等于多少呢？
有一个定理叫二项式定理，它给出了答案：

\[\begin{aligned} (a+b)^n& =\dbinom{n}{0}a^{n}b^{0}+\dbinom{n}{1}a^{n-1}b^{1}+\cdots+\dbinom{n}{n}a^{0}b^{n}\\ (a+b)^n&=\sum_{i=0}^n\binom{n}{i}a^{n-i}b^i \end{aligned} \]

很显然 \(a,b\) 可以交换，即：

\[(a+b)^n=\sum_{i=0}^n\binom{n}{i}b^{n-i}a^i \]

为什么有二项式定理？不会证（逃
扩展一下：

\[\begin{aligned} (ax+by)^n=\sum_{i=0}^n\binom{n}{i}(ax)^{n-i}(by)^i \end{aligned}\]

定理 2.8： Lucas 定理

证明在这

3. 组合数求法（带取模）

• \(n,m\) 范围可预处理出阶乘值
  此时直接套公式算即可。
  不过要注意：因为我们在取模意义下求解组合数值，因此 \(\frac{1}{(m)!(n-m)!}\) 要变为 \((m)!(n-m)!\) 的逆元，用扩欧求解即可（模数一定时也可以用快速幂）。

ll jc[N];//阶乘
ll x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll d=exgcd(b,a%b,y,x);
	y=y-a/b*x;
	return d;
}
ll C(int n,int m){
  if(m>n)return 0;//n里取出比n还多的个数是不可能的，因此输出 0
	ll upp=jc[n-m]*jc[m]%mod;//除数
	ll d=exgcd(upp,mod,x,y);//求解除数的逆元
	while(x<=0){
		x+=mod/d;
	}
	x=x%(mod/d);
	return jc[n]*x%mod;//乘上逆元即可
}  
...  
jc[0]=1;//预处理阶乘
for(int i=1;i<=n;i++){
	jc[i]=jc[i-1]*i%mod;
}

• \(n\) 和 \(m\) 大小相差很远或 \(n,m\) 大小很接近（\(n-m\) 或 \(m\) 的值要在可接受的范围内）
  回头看公式：\(\dbinom{n}{m}=\dfrac{n!}{m!(n-m)!}\)，我们尝试将 \((n-m)!\) 与 \(n!\) 约去一部分，原式就变成了：\(\dbinom{n}{m}=\dfrac{n\times (n-1)\times \cdots \times (n-m+1)}{m!}\)
  此时由于 \(n\) 和 \(m\) 大小相差很远，因此计算 \(n\times (n-1)\times \cdots \times (n-m+1)\) 并不需要消耗太多时间，因此直接算阶乘然后乘逆元即可。
  以下代码顺便演示快速幂求解逆元的方法（需要模数为质数）

ll ksm(ll a,ll b){
	ll ans=1;
	while(b){
		if(b&1==1){
			ans=(ans%mod*a%mod)%mod;
		}
		a=(a%mod*a%mod)%mod;
		b>>=1;
	}
	return ans%mod;
}
ll inv=1;
ll C(ll n,ll m){
	if(n<m)return 0;
	ll jc1=1;
	for(ll i=n;i>=(n-m+1);i--){//用公式暴力计算阶乘
		jc1=(jc1%mod*(i%mod))%mod;
	}
	return (jc1%mod*ksm(m,p-2)%mod)%mod;//乘上 m! 的逆元
}

对于 \(n,m\) 大小很接近的情况，只需利用公式：\(\dbinom{n}{m}=\dbinom{n}{n-m}\)。由于 \(n,m\) 大小接近，因此把求解 \(\dbinom{n}{m}\) 转化为 \(\dbinom{n}{n-m}\)，此时 \(n\) 与 \(n-m\) 一定相差很远，转换为上文的情况。

• 使用 Lucas 定理（模数值较小且是质数的情况）
  Lucas 定理把 \(n,m\) 转换成 \(p\) 进制来求解，可以极大减少时间复杂度。
  模板直接上代码：

ll jc[N];
ll n,m,p;
ll x,y;
ll exgcd(ll a,ll b,ll &x,ll &y){
	if(b==0){
		x=1;
		y=0;
		return a;
	}
	ll d=exgcd(b,a%b,y,x);
	y=y-(a/b)*x;
	return d;
}
ll inv(ll a){
    ll d=exgcd(a,mod,x,y);
    while(x<0){
        x+=mod/d;
    }
    x%=mod/d;
    return x;
}
ll cmn(ll ni,ll mi){//在范围内求解逆元，介绍的第一种方法，不在赘述了
	if(ni<mi)return 0;
	return jc[ni]*inv((jc[mi]*jc[ni-mi])%mod)%mod;
}
ll lucas(ll n,ll m){
	if(n<mod&&m<mod){
		return cmn(n,m);//边界条件内可以直接求解
	}
	return (lucas(n%mod,m%mod)*lucas(n/mod,m/mod))%mod;//分解进制接着向下求解
}

当模数不一定是质数（意味着逆元可能不存在），\(n,m\) 中有一个较小（ \(\le 5000\)），下面假设 \(m\) 较小。
首先可以知道变成阶乘除法后分子和分母中最多一定会有 \(m\) 项。
然后因为模数不一定是一个质数，因此不能直接算逆元，那么怎么办？
组合数一定是一个整数，那么我们就直接尝试将这个分数约分，也就是两两之间尝试除以两者的最大公约数。
操作完成后，分母一定是 \(1\)，然后将分子乘起来即可。

4. 插板法专题

中心思想：将给盒子分物品转化为给物品分盒子。

例1

五个相同的同学分到三个不一样的班级，每个班级至少分到 \(1\) 人，有几种分法？
首先我们画出 \(5\) 个圆圈表示这五个人：

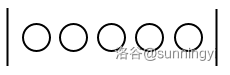
这时候我们想象这些同学的两边有隔板，我们可以通过放置一些隔板来把这些同学分组，如图：

此时我们如果放入一个隔板：

可以发现，如果我们插入 \(n\) 个板，可以分出 \(n+1\) 组来。
此时我们把分出来的每个组看成每个班，就可以把给每个班分同学的问题转化为通过插入隔板将同学分到每个班的过程。
也就是说，此时我们要求的就是在这些同学之间插板的方案数。容易发现，当有 \(n\) 个同学时，可以在 \(n-1\) 个地方插入隔板，要分 \(m\) 个班，就要插入 \(m-1\) 个隔板。
于是方案数为：

\[\binom{n-1}{m-1} \]

例2

五个相同的同学分到三个不一样的班级，班级可以没有人，有几种分法？
还能沿用 例1 的思路吗？由于每个班可以没有同学，因此我们在插入一个隔板来，反而会多出两个插板位置来：

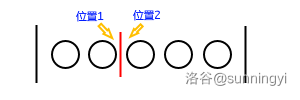
但是此时可以发现：不管是向位置 \(1\) 还是位置 \(2\) 插入隔板都不会影响情况，那么可不可以认为放入一个隔板后并不会影响放入位置的总数量，可以直接使用 \(可放入位置数^{插入板的个数}\) 来计算呢？
其实是不可以的，如图，图下的序号代表第几个插板：

也就是说，并不是每一个插板都可以放在全部的位置，部分位置会造成统计的重复。
那怎么办，我们不妨"借"三个"假人" 过来，情况变成这样：

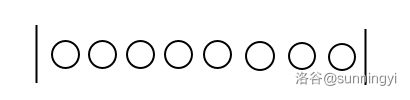
此时我们可以把这个问题变成：将这总共八个人分到三个班，每班至少一人的方案数。
这样是如何考虑”没有人“的情况的呢？其实这里的”每班至少一人“和"借三个假人"相当于给每个班的人数上了一个”保底“，每班都至少可以分到一人，这是我们只需在每种情况中去掉那一个保底，即把每个班的人数减一，就可以求解出只分那五个真人的情况。
由于 例1 中的统计方法可以被证明不会重复，那么将这里每种选法中选出来的人数的方案中每个班的人数减一所形成的方案数自然也是不会重复的，因此可以说明这种方法的正确性。
综合上文，我们得出：将 \(n\) 个相同的人分成 \(m\) 个不同的班级，每个班可以没有人的情况数为：

\[\binom{n+m-1}{m-1}=\binom{n+m-1}{n} \]

例3：一般情况

我们来讨论上面两例的一般情况，即 五个相同的同学分到三个不一样的班级，第 \(i\) 个班级至少要分到 \(a_i\) 个人，保证 \(\sum_{i=1}^{3} a_i \le 5\) ，有几种分法？
此时我们也可以用”借“的思想来考虑：由于我们要保证每个班又要有那个最少人数，且同学们之间没有任何区别，那我们不妨先从所有同学中把那每个班最少要的 \(a_i\) 个同学先拿出来给到每个班，这样也相当与一个保底，此时我们可以把问题变成：\(5-\sum_{i=1}^{3} a_i\) 个人分到 \(3\) 个班，每班可以不分人的情况数。
根据我们在 例2 的讨论，答案是 \(\dbinom{5-\sum_{i=1}^{3} a_i +3-1}{3-1}\)，这个式子的结果就是原问题的答案。
于是总结一般规律：将 \(n\) 个人分成 \(m\) 个班，第 \(i\) 个班至少要分 \(a_i\) 个人，且保证 \(\sum_{i=1}^n a_i \le n\)，此时方案数为：

\[\dbinom{n-\sum_{i=1}^{n} a_i +m-1}{m-1} \]

例4：抽象为代数问题

上述的计数问题，本质上是一次不定方程正整数解计数问题。
什么是一次方程？说人话就是多元一次方程。
也就是形如 \(x_1+x_2+\cdots +x_m=n\) 的方程，求 \(x_1\sim x_m \ \ (x\in \mathbb{Z})\) 这一个解的组合不同的个数。
对于 例1，抽象成不定方程为：

\[x_1+x_2+\cdots+x_m=n \ \ \ (x_i \ge 1,x\in \mathbb{Z}) \]

求解 \(x_1\sim x_m\) 这一个解的组合不同的个数。

对于 例2：

\[x_1+x_2+\cdots+x_m=n \ \ \ (x_i \ge 0,x\in \mathbb{Z}) \]

求解 \(x_1\sim x_m\) 这一个解的组合不同的个数。

对于 例3：

\[x_1+x_2+\cdots+x_m=n \ \ \ (x_i \ge 0,x_i\ge a_i,x\in \mathbb{Z}) \]

求解 \(x_1\sim x_m\) 这一个解的组合不同的个数。

例5

存在上界的不定方程正整数解计数问题。
CF451E Devu and Flowers
【好题选讲】CF451E Devu and Flowers

5. 错排问题

问题：把 \(n\) 个数放到标有 \(1\sim n\) 的盒子中，没有数放在和它标号相同的盒子中，多少种情况？

\[F_n=(n-1)(F_{n-1}\times F_{n-2}) \]

6. Catalan 数

卡特兰数表示为 \(H_n\)。

\[H_n=\frac{\binom{2n}{n}}{n+1} \]

或者：

\[H_n=\sum_{i=1}^{n} H_{i-1}\times H_{n-i} \]

\[H_n=\binom{2n}{n}-\binom{2n}{n-1} \]

情况：

• \(n\) 个节点的二叉树，不同形状的数量的个数？
• \(n\) 个元素出栈，情况数？
• 有 \(2n\) 个人入场，入场费 \(m\) 元，每人带着 \(m,2m\) 面值的钞票，初始售票处没有零钱，多少种入场给钱的顺序，使得不会没钱可找？
• 一个矩形，只能右下走，不能走到对角线上面，从左上走到右下多少种走法？
• 凸矩形，能画出多少不同的三角形？

7. 第二类斯特林数

第二类斯特林数表示为 \(S(n,k)\)（大写的 S）。
递推公式：

\[S(n,k)=S(n-1,k-1)+k\times S(n-1,k) \]

情况：

• \(n\) 个不同的元素，放到 \(k\) 个相同的（不同的）非空（可空）集合中，多少种情况？

---

迁移自洛谷