Tarjan学习笔记

tarjan学习笔记

有向图

• 基础定义

  • 有向图的强连通

    • 1.强连通：在有向图中，设两点\(a,b\)均有一条路到达另一个点，就叫 \((a,b)\) 强连通

      2.强连通图：若在一个有向图\(G\)中，任意两个点强连通，就叫 \(G\) 是一个强连通图

      3.强连通分量(scc)：非联通有向图中尽可能大的强连通子图，称作强连通分量

  • 有向图的DFS树

    • 对图深搜时，每个节点遍历一次，遍历过的点和边构成搜索树

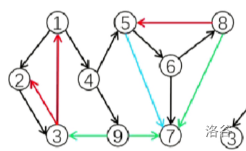
    • 有向图的DFS树的四种边(不一定同时出现):

      • (1).树边(黑色): 遍历（前往）节点时经过的边;

        (2).返祖边\后向边(红色): 子节点指向祖先节点的边;

        (3).前向边(蓝色)：父节点指向子孙节点的边;

        (4).横插边(绿色)：右子树指向左子树的边 指向兄弟节点的边(有向);
        

    • 性质：

      • 返祖边必和树边形成环;横插边可能和树边形成环

    • 时间戳：用于标记每个节点在进栈时的被访问顺序（有小到大）,用\(dfn[u]\)表示;

    • 追溯值：用来表示以当前节点为根节点的搜索树的根节点出发，能够访问到的所有节点中，时间戳最小的值，用 \(low[u]\) 表示;

    • 当一个点的dfn[u]和low[u]相等时，以u为根节点的搜索树中的全部节点（从栈顶到u）是一个强连通分量(可以停下思考一下为什么)

  • Tarjan求有向图的强连通分量

    Tarjan是什么：

    Tarjan算法的基本思路对于每个点，尽量找到与它一起能构成环的所有节点
    Tarjan基于DFS。每个强连通分量是搜索树的一颗子树，
    搜索时，把当前搜索树中未处理的节点加入一个栈，回溯时判断栈顶到栈中的节点是否是一个强连通分量

  • 追溯值的求法

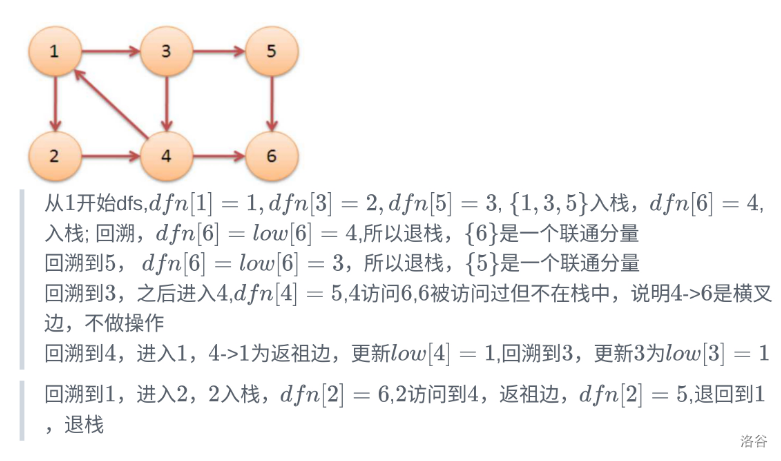
    • 若边x ->y是树边（且没有被访问过），则有 \(low[x]=min(low[x],low[y])\) ;

      若边x ->y是返祖边（被访问过且在栈中），则有 \(low[x]=min(low[x],dfn[y])\) ;

      若边x ->y是横插边（且不在栈中），无需维护;

      例：
      

  • 算法过程

    • 遍历点x的时候，盖戳，入栈；

    • 遍历x可以到达的点y，分以下三种情况：

      • (1).y未被访问过：对y进行深搜，更新low[y],并更新 \(low[x]=min(low[x],low[y])\);

        (2).y被访问过且y在栈中：推理得y是x的祖先节点或x兄弟子树上的节点（即x ->y是横插边），所以 \(low[x]=min(low[x],dfn[y])\) ;

        (3).y被访问过且y不在栈中：y在其他强连通分块中，不需要处理;

    • 当y点遍历完后，判断以x为根的搜索树是否是scc，如果是，退栈并更新cnt(scc个数)的值;

  • 代码实现

    • 用vector存的图 我不会说是因为我不会链式前向星
    1

    ~~~cpp void tarjan(int x){ dfn[x]=low[x]=++tot;//x盖戳 stk[++top]=x;//x入栈 ifstk[x]=1;//标记x在栈中 for(int i=0;i

  • 时间复杂度

    • 每个节点只遍历一遍且每条边只遍历一遍所以时间复杂度为 \(O(N+M)\)

  • 基础理论完结，撒花~~

例题

• luogu P2863 The Cow Prom S

  题目描述

  有一个 \(n\) 个点，\(m\) 条边的有向图，请求出这个图点数大于 \(1\) 的强连通分量个数。

  输入格式

  第一行为两个整数 \(n\) 和 \(m\)。

  第二行至 \(m+1\) 行，每一行有两个整数 \(a\) 和 \(b\)，表示有一条从 \(a\) 到 \(b\) 的有向边。

  输出格式

  仅一行，表示点数大于 \(1\) 的强连通分量个数。

  样例 #1

  样例输入 #1

  5 4
  2 4
  3 5
  1 2
  4 1
  

  样例输出 #1

  1
  

  提示

  数据规模与约定

  对于全部的测试点，保证 \(2\le n \le 10^4\)，\(2\le m\le 5\times 10^4\)，\(1 \leq a, b \leq n\)。

  题目分析

  题目简洁明了，直接跑一遍Tarjan，判断每个强连通分量的siz即可；
  注意，需要在每个点作为搜索树的根，因为可能存在不连通的情况\

  代码来喽~~

  2

  #include <bits/stdc++.h>
  using namespace std;
  const int N=1e6+10;
  int dfn[N],stk[N],low[N],ifstk[N],scc[N],siz[N],tot,top,cnt;
  vector <int> vet[N];
  void tarjan(int x){
      dfn[x]=low[x]=++tot;
      stk[++top]=x;
      ifstk[x]=1;
      for(int i=0;i<vet[x].size();i++){
          int y=vet[x][i];
          if(!dfn[y]){
              tarjan(y);low[x]=min(low[x],low[y]);
          }else if(ifstk[y]){
              low[x]=min(low[x],dfn[y]);
          }
      }
      if(dfn[x]==low[x]){
          ++cnt;int y;
          do{
              y=stk[top  -  -];
              ifstk[y]=0;
              scc[y]=cnt;
              siz[cnt]++;
          }while(y!=x);
      }
  }
  int main(){
      int n,m,a,b,ans=0;
      cin>>n>>m;
      for(int i=1;i<=m;i++){
          cin>>a>>b;
          vet[a].push_back(b);
      }
      for(int i=1;i<=n;i++)
          if(!dfn[i])tarjan(i);
      for(int i=1;i<=cnt;i++)
          if(siz[i]>1)
              ans++;
      cout<<ans;
  }
  

• P2341 [USACO03FALL / HAOI2006] 受欢迎的牛 G

  题目描述

  每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果 \(A\) 喜欢 \(B\)，\(B\) 喜欢 \(C\)，那么 \(A\) 也喜欢 \(C\)。牛栏里共有 \(N\) 头奶牛，给定一些奶牛之间的爱慕关系，请你算出有多少头奶牛可以当明星。

  输入格式

  第一行：两个用空格分开的整数：\(N\) 和 \(M\)。

  接下来 \(M\) 行：每行两个用空格分开的整数：\(A\) 和 \(B\)，表示 \(A\) 喜欢 \(B\)。

  输出格式

  一行单独一个整数，表示明星奶牛的数量。

  样例 #1

  样例输入 #1

  3 3
  1 2
  2 1
  2 3
  

  样例输出 #1

  1
  

  提示

  只有 \(3\) 号奶牛可以做明星。

  【数据范围】

  对于 \(10\%\) 的数据，\(N\le20\)，\(M\le50\)。

  对于 \(30\%\) 的数据，\(N\le10^3\)，\(M\le2\times 10^4\)。

  对于 \(70\%\) 的数据，\(N\le5\times 10^3\)，\(M\le5\times 10^4\)。

  对于 \(100\%\) 的数据，\(1\le N\le10^4\)，\(1\le M\le5\times 10^4\)。

  题目分析

  看完题目，是不是完全看不出来和Tarjan有什么关系？
  没关系，只需要补充一个思想/操作：缩点
  缩点： 把每个scc当成一个大点来处理，将原图变为有向无环图（DAG）

  缩点后，再看回题目，其实就是找缩点之后是否有且仅有一个出度为0的scc

  为什么呢？我们考虑对于缩点之后的DAG，一定有任意两个点是非强连通的（记住这个前提，很重要），若这两个点是强联通的，那么这两个点应当位于同一个强连通分量里

  对于DAG分成三种情况考虑：

  1.该图是非联通的，那一定不存在明星牛，过于简单，不予证明

  2.该图是联通的且有多个出度为零的大点，这些出度为零的大点之间不连通，所以这些大点中没有一个是明星牛

  3.该图是联通的且仅有一个出度为零的大点,那么一定所有的点都有到达这个点的路径

  如果一个大点出度不为0，那么它指向的大点一定无法指向它（因为这两个大点不是强联通的），也就一定不是明星牛了

  找到出度为零的大点后，对于被这个大点包含的奶牛都是明星牛（在同一个scc里每个点都可以互相到达）

  所以问题就转化成了判断缩点之后是否有且仅有一个出度为0的scc，如果有多个或没有，输出0，否则输出出度为零的scc 的大小；

  代码实现

  3

  #include <bits/stdc++.h>
  using namespace std;
  const int N=1e6+10;
  int dfn[N],stk[N],a[N],b[N],dout[N],din[N],low[N],ifstk[N],scc[N],siz[N],tot,top,cnt;
  vector <int> vet[N];
  void tarjan(int x){
      dfn[x]=low[x]=++tot;
      stk[++top]=x;
      ifstk[x]=1;
      for(int i=0;i<vet[x].size();i++){
          int y=vet[x][i];
          if(!dfn[y]){
              tarjan(y);low[x]=min(low[x],low[y]);
          }else if(ifstk[y]){
              low[x]=min(low[x],dfn[y]);
          }
      }
      if(dfn[x]==low[x]){
          ++cnt;int y;
          do{
              y=stk[top  -  -];
              ifstk[y]=0;
              scc[y]=cnt;
              siz[cnt]++;
          }while(y!=x);
      }
  }
  int main(){
      int n,m,ans=0;
      cin>>n>>m;
      for(int i=1;i<=m;i++){
          cin>>a[i]>>b[i];
          vet[a[i]].push_back(b[i]);
      }
      for(int i=1;i<=n;i++)
          if(!dfn[i])tarjan(i);
      for(int i=1;i<=m;i++){
          if(scc[a[i]]!=scc[b[i]]){
              dout[scc[a[i]]]++;
              din[scc[b[i]]]++;
          }
      }
      int sum=0;
      for(int i=1;i<=cnt;i++){
          if(!dout[i]){
              ans=siz[i];
              ++sum;
          }
      }
      if(sum>1)ans=0;
      cout<<ans;
      return 0;
  }
  

• P3387 【模板】缩点

  题目描述

  给定一个 \(n\) 个点 \(m\) 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

  允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

  输入格式

  第一行两个正整数 \(n,m\)

  第二行 \(n\) 个整数，其中第 \(i\) 个数 \(a_i\) 表示点 \(i\) 的点权。

  第三至 \(m+2\) 行，每行两个整数 \(u,v\)，表示一条 \(u\rightarrow v\) 的有向边。

  输出格式

  共一行，最大的点权之和。

  样例 #1

  样例输入 #1

  2 2
  1 1
  1 2
  2 1
  

  样例输出 #1

  2
  

  提示

  对于 \(100\%\) 的数据，\(1\le n \le 10^4\)，\(1\le m \le 10^5\)，\(0\le a_i\le 10^3\)。

  题目分析

  这回是正经缩点模板，不多废话，上代码

  代码实现

  4

  #include <bits/stdc++.h>
  using namespace std;
  const int N=1e5+10;
  int dfn[N],stk[N];
  int w[N],new_w[N],dp[N];
  int dout[N],din[N];
  int low[N],ifstk[N],scc[N],siz[N];
  int a,b,tot,top,cnt;
  vector <int> vet[N],new_vet[N];
  void tarjan(int x){
      dfn[x]=low[x]=++tot;
      stk[++top]=x;
      ifstk[x]=1;
      for(int i=0;i<vet[x].size();i++){
          int y=vet[x][i];
          if(!dfn[y]){
              tarjan(y);low[x]=min(low[x],low[y]);
          }else if(ifstk[y]){
              low[x]=min(low[x],dfn[y]);
          }
      }
      if(dfn[x]==low[x]){
          ++cnt;int y;
          do{
              y=stk[top  -  -];
              ifstk[y]=0;
              scc[y]=cnt;
              siz[cnt]++;
          }while(y!=x);
      }
  }
  int main(){
      int n,m,ans=0;
      cin>>n>>m;
      for(int i=1;i<=n;i++)
          cin>>w[i];
      for(int i=1;i<=m;i++){
          cin>>a>>b;
          vet[a].push_back(b);
      }
      for(int i=1;i<=n;i++)
          if(!dfn[i])tarjan(i);
      for(int x=1;x<=n;x++){//缩点
          new_w[scc[x]]+=w[x];//合并点权
          for(int y : vet[x])
              if(scc[x]!=scc[y])
                  new_vet[scc[x]].push_back(scc[y]);//建边
      }
      for(int x=cnt;x;x  -  -){
          if(dp[x]==0)//x是出发点之一
              dp[x]=new_w[x];
          for(int y : new_vet[x])
              dp[y]=max(dp[y],dp[x]+new_w[y]);//DP跑最长路
      }
      for(int i=1;i<=n;i++)
          ans=max(ans,dp[i]);//统计
      cout<<ans;
      return 0;
  }
  

无向图

• 基础定义

  • 给定连通图\(G=(V,E)\)：
    割点：若对于节点\(x \in V\)，从图中删去节点\(x\)以及所有与\(x\)关联的边后\(G\)分裂成两个或两个以上不相连的子图，则称\(x\)为\(G\)的割点

    割边/桥：若对于边\(e \in E\)，从图中删去边\(e\)之后，\(G\)分裂成两个不相连的子图，则称\(e\)为\(G\)的桥或割点

    一般无向图(不一定连通)的“割点”和“桥”就是它的各个连通块的“割点”和“桥”。

  • 割边判断法则

    • 无向边\((x,y)\)是桥，当且仅当搜索树上存在\(x\)的一个子节点\(y\)，满足：$$ dfn[x]<low[y]$$

      根据定义，\(dfn[x]<low[y]\) 说明从\(y\)开始的搜索树出发，在不经过\((x,y)\)的前提下，不管走哪条路，都无法到达\(x\)或比\(x\)更早访问的节点。若把\((x,y)\)删除，则从\(y\)开始的搜索树无法与节点\(x\)没有边相连，图断开成了两部分，因此\((x,y)\)是割边

      桥一定是搜索树中的边，并且一个简单环中的边一定都不是桥

    • 判断是不是桥要注意判断重边，如果是重边则一定不是桥

      这个是我写的，码风不太好

      #include <bits/stdc++.h>
      using namespace std;
      const int SIZE =1E5+10;
      int head[SIZE],ver[SIZE*2],Next[SIZE*2];
      int dfn[SIZE],low[SIZE],n,m,tot,num;
      bool bridge[SIZE*2];
      void add (int x,int y){
          ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
      }
      void tarjan(int x,int in_edge){
          dfn[x]=low[x]=++num;
          for(int i=head[x];i;i=Next[i]){
              int y=ver[i];
              if(!dfn[y]){
                  tarjan(y,i);
                  low[x]=min(low[x],low[y]);
                  if(low[y]>dfn[x])
                      bridge[i]=bridge[i^1]=1;
                  
              }
              else if(i!=(in_edge^1))
                  low[x]=min(low[x],dfn[y]);
          }
      }
      int main(){
          cin>>n>>m;
          tot=1;
          for(int i=1;i<=m;i++){
              int x,y;
              cin>>x>>y;
              add(x,y);add(y,x);
          }
          for(int i=1;i<=n;i++)
              if(!dfn[i])tarjan(i,0);
          for(int i=2;i<tot;i+=2)
              if(bridge[i])
                  cout<<ver[i^1]<<' '<<ver[i]<<endl;
      }
      

      有个更好的解决方案，可惜没看懂，有能力的看完给我讲一讲哈
      记录“递归进入每个节点的边的编号”。编号可认为是边在邻接表中的存储的下表位置。把无向图的每一条边当做双向边，成对储存在下标“2，3”“4，5”“6，7”……处。若沿着编号为 \(i\) 的边递归进入了节点\(x\)，则忽略从 \(x\) 出发的编号为 \(i xor 1\) 的边，通过其他边计算 \(low[x]\) 即可

      注：此码不会按字典序输出桥

      #include <bits/stdc++.h>
      using namespace std;
      const int SIZE =1E5+10;
      int head[SIZE],ver[SIZE*2],Next[SIZE*2];
      int dfn[SIZE],low[SIZE],n,m,tot,num;
      bool bridge[SIZE*2];
      void add (int x,int y){
          ver[++tot]=y,Next[tot]=head[x],head[x]=tot;
      }
      void tarjan(int x,int in_edge){
          dfn[x]=low[x]=++num;
          for(int i=head[x];i;i=Next[i]){
              int y=ver[i];
              if(!dfn[y]){
                  tarjan(y,i);
                  low[x]=min(low[x],low[y]);
                  if(low[y]>dfn[x])
                      bridge[i]=bridge[i^1]=1;
                  
              }
              else if(i!=(in_edge^1))
                  low[x]=min(low[x],dfn[y]);
          }
      }
      int main(){
          cin>>n>>m;
          tot=1;
          for(int i=1;i<=m;i++){
              int x,y;
              cin>>x>>y;
              add(x,y);add(y,x);
          }
          for(int i=1;i<=n;i++)
              if(!dfn[i])tarjan(i,0);
          for(int i=2;i<tot;i+=2)
              if(bridge[i])
                  cout<<ver[i^1]<<' '<<ver[i]<<endl;
      }
      

  • 割点判定法则

    • 若\(x\) 不是搜索树的根节点，则\(x\)是割点当且仅当线段树上存在\(x\)的一个子节点\(y\)，满足：$$dfn[x] \leqslant low[y]$$

      特别的，若\(x\)是搜索树的根节点，则\(x\)是割点当且仅当搜索树上至少存在两个子节点\(y_{1},y_{2}\)满足以上条件。

--大量借鉴此片PDF和部分借鉴《算法竞赛进阶指南》

写的不好勿骂>.<