算法
解题方案的准确而完整的描述
基本特征
可行性：能解决问题
确定性：每个步骤必须是明确定义的，不许模棱两可，也不许有多义性
有穷性：算法必须在有限时间内做完，在执行有限个步骤后终止
拥有足够的情报：要有一定的输入数据，必须 有输出结果
基本要素
对数据对象的运算和操作：算术运算（+-*÷）逻辑运算 关系运算（大小）数据传输（a=b）
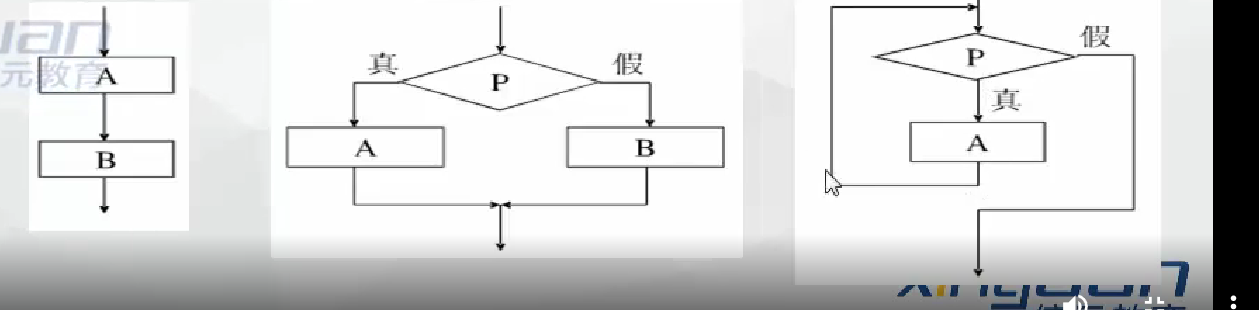
算法的控制结构：顺序 选择 循环
分析算法
常用时间复杂度和空间复杂度表示
目的：降低两个度，提高执行效率
时间复杂度
可以用算法所执行的基本运算次数度量。与问题和问题的规模有关（两个杯子 三个杯子
例 交换两个杯子中的水，基本运算次数是3
分析算法工作量的方法：
空间复杂度
执行算法所需要的内存空间。包括算法程序 输入的初始数据 执行过程中需要的额外空间（杯子c
数据结构
相互有关联的数据元素的集合
逻辑结构
包含两个要素
线性结构
线性表，栈，队列
条件
有且只有一个根结点，它无前件
有且只有一个终端(叶子)结点，它无后件
除根结点和叶子结点外，其它结点有且只有一个前件，也有且只有一个后件
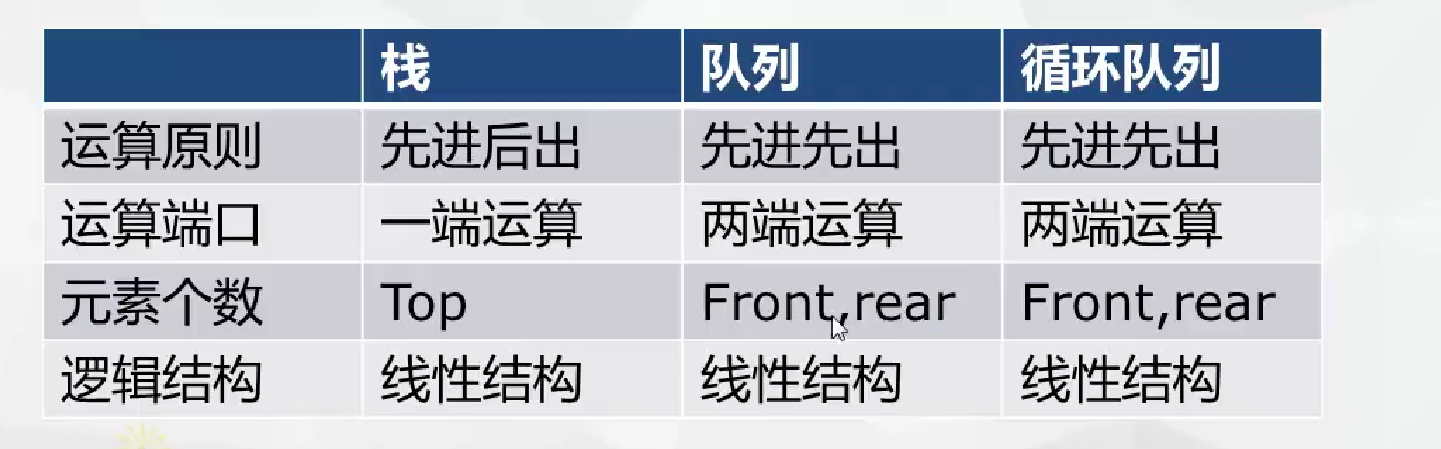
栈
限定在一端进行插入和删除的线性表。原则是先进后出 或后进先出。具有记忆功能
栈运算
队列
是指允许在一端进行插入，而在另一端进行删除的线性表。原则是先进先出 或后进后出
- 循环队列
将队列存储空间的最后一个位置绕道第一个位置，形成逻辑上的环状空间
比较
非线性结构
树
树是n(n>0)个元素的有限集合。它有且仅有一个称为根的元素；其余元素是互不相交的子树
父结点：每个结点只有一个前件，为父结点
根结点：没有前件的结点（只有一个）
子节点：每个结点的后件可以有多个，称为子节点
叶子节点：没有后件的结点
结点的度：一个结点所拥有的后件的个数
树的度：所有结点中最大的度称为树的度
树的深度：树的最大层次
二叉树
非空二叉树只有一个根结点，每个结点最多有两棵子树（度最大是2）分别称为左子树和右子树
- 满二叉树
每一层上的结点数均达到最大值
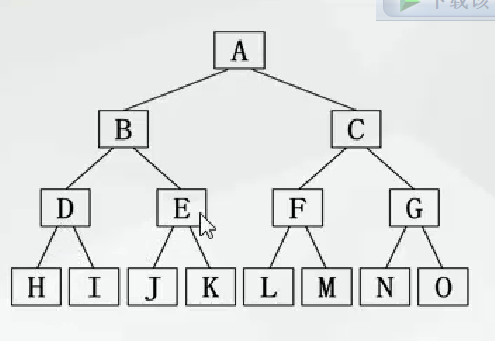
- 完全二叉树
只缺少最后一层右边的若干结点
编号为k的结点左子结点为2k，右子结点为2k+1
编号为k的结点的父结点变好为k/2
- 二叉树的遍历
从某一个结点出发，依次访问到二叉树的所有结点
前序遍历：访问根结点 前序遍历左子树 前序遍历右子树
中序遍历：中序遍历左子树 访问根结点 中序遍历右子树
8 4 9 2 10 5 1 6 3 7
后序遍历：后序遍历左子树 后序遍历右子树 访问根结点
8 9 4 10 5 2 6 7 3 1
存储结构
指数据的逻辑结构在计算机存储空间中的存放形式。一种数据结构的逻辑结构根据需要可以表示成多种存储结构。不同的存储结构，数据处理的效率是不同的
顺序存储
空间是连续的
顺序表
线性表的顺序存储
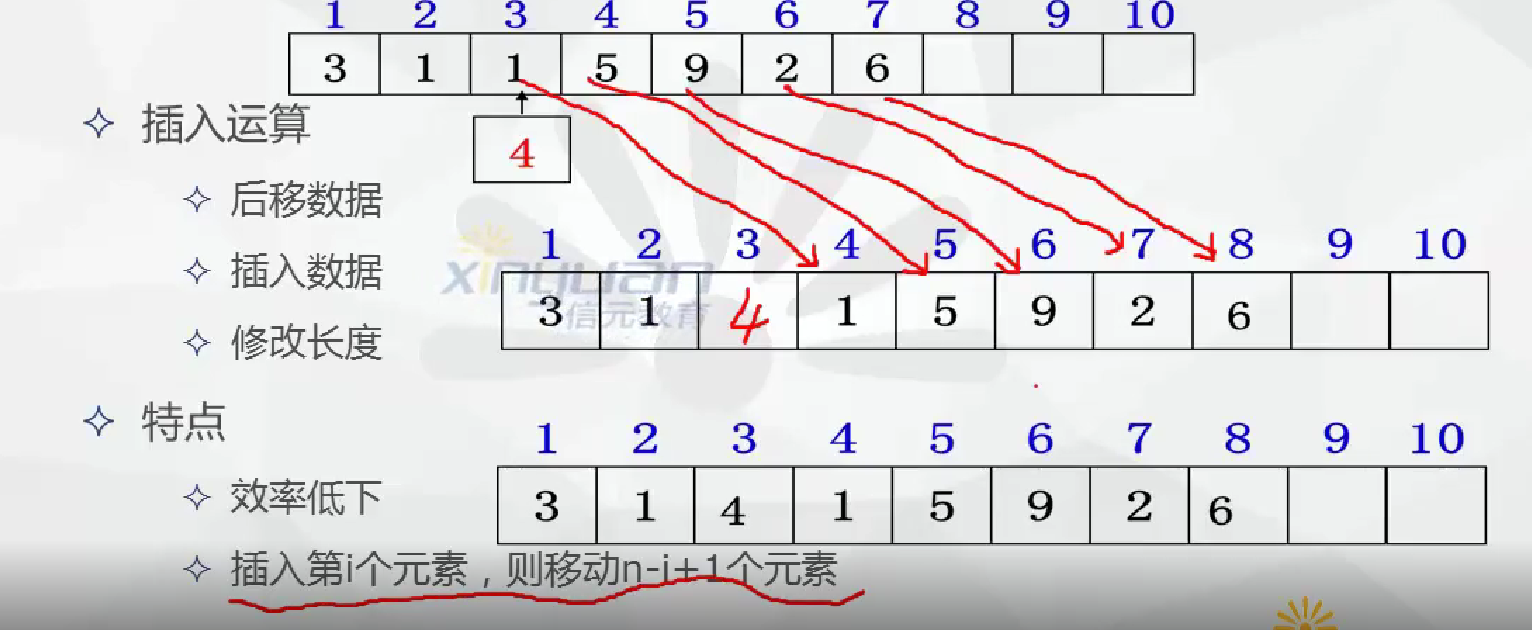
- 插入运算
- 删除运算
链式(接)存储
不需要连续的存储空间，但需要额外的空间放小纸条
线性链表
线性表的链式存储结构
- 单链表
- 带头结点的单链表
空间换时间 - 循环链表
- 双向链表
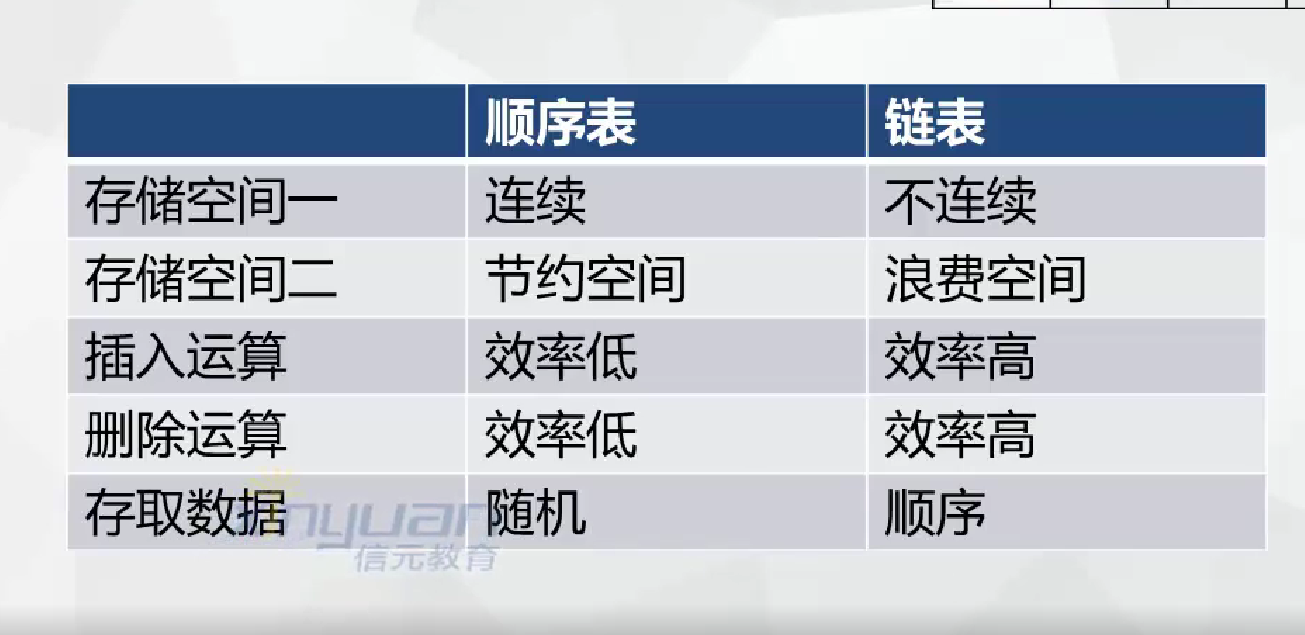
- 比较
运算
插入
删除
查找
顺序查找
适用于无序表或链式线性表。在最坏情况下进行n次比较
二分（对分）查找
数据必须是排好序的
即使是有序线性表，如果采用链式存储结构，也只能用顺序查找
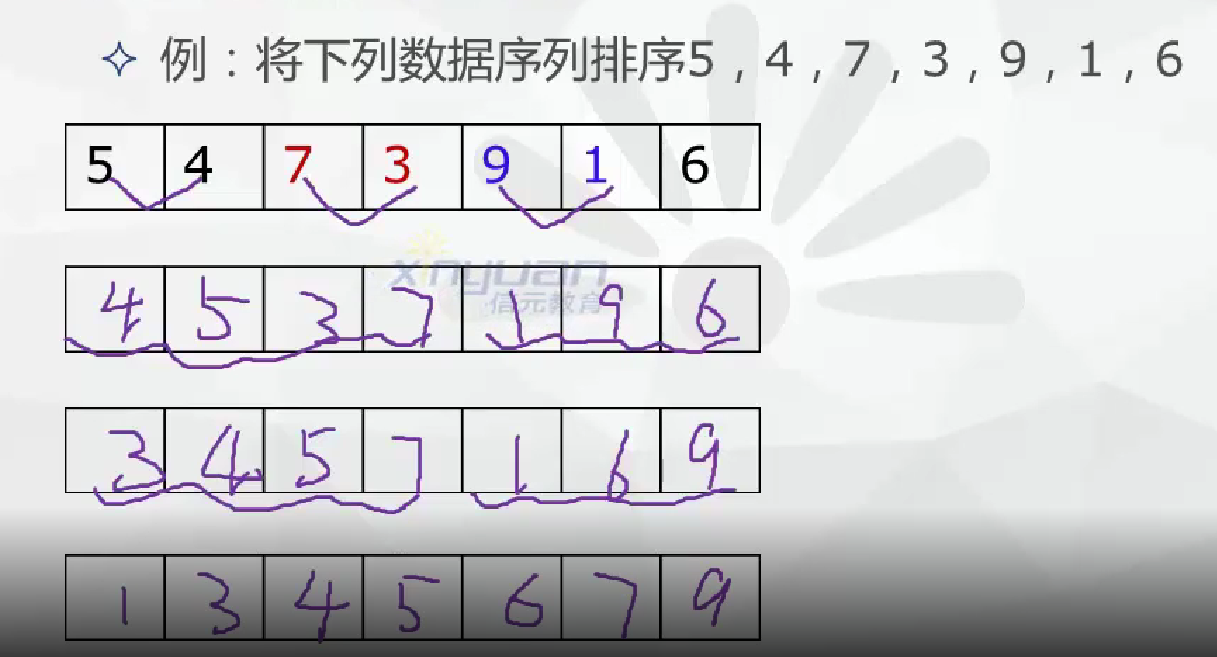
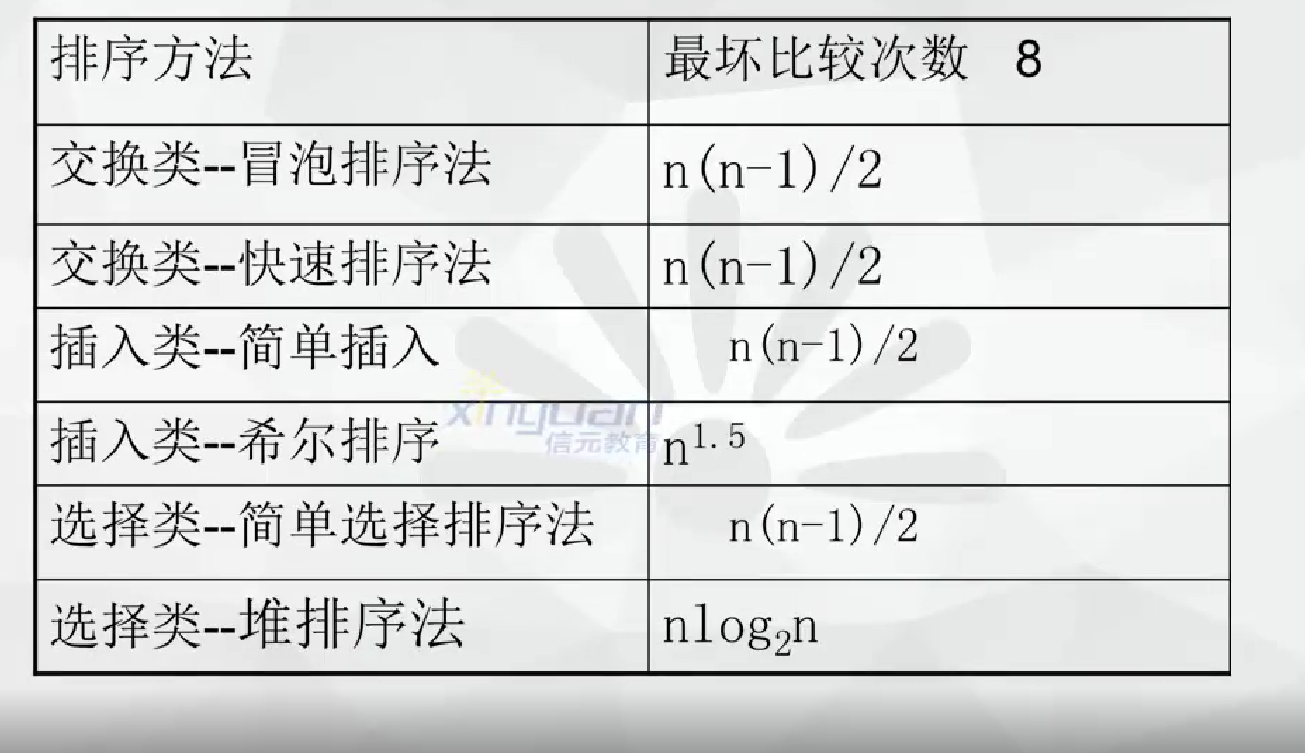
排序
交换类排序法
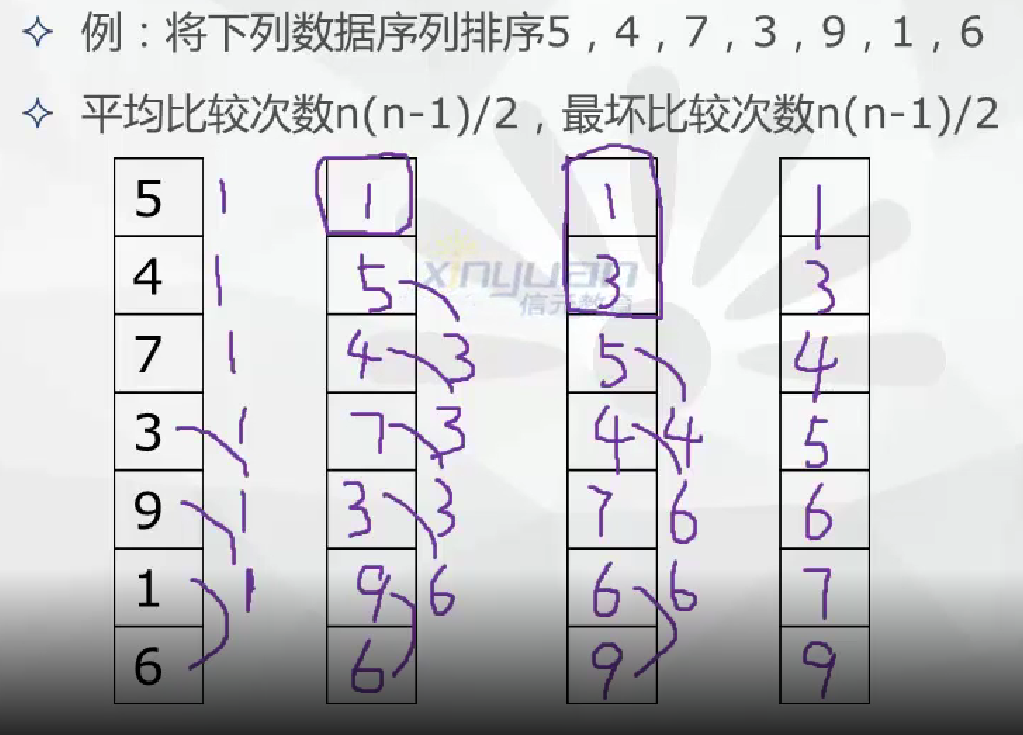
- 冒泡排序法
借助数据元素之间的互相交换进行排序的一种方法
- 快速排序
选择一个元素T,将小于T的元素移动到T前面，将大于T的元素移动到T的后面
插入类排序法
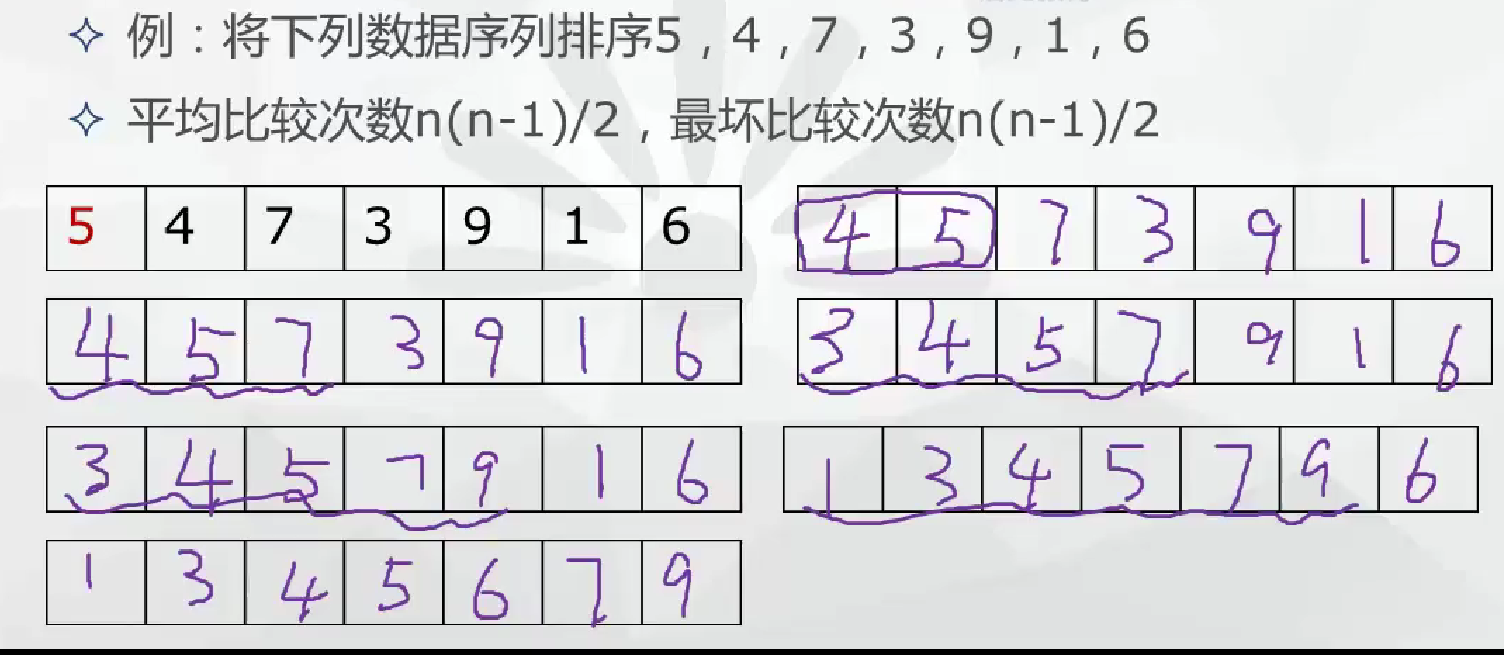
- 简单插入排序法
将无序列表中的各元素依次插入到已经有序的线性表中
- 希尔排序法
选择类排序法
- 简单选择排序法
扫描整个表，从表中选一个最小的放到表的前面，剩下的表采用同样的方法，直到子表为空为止
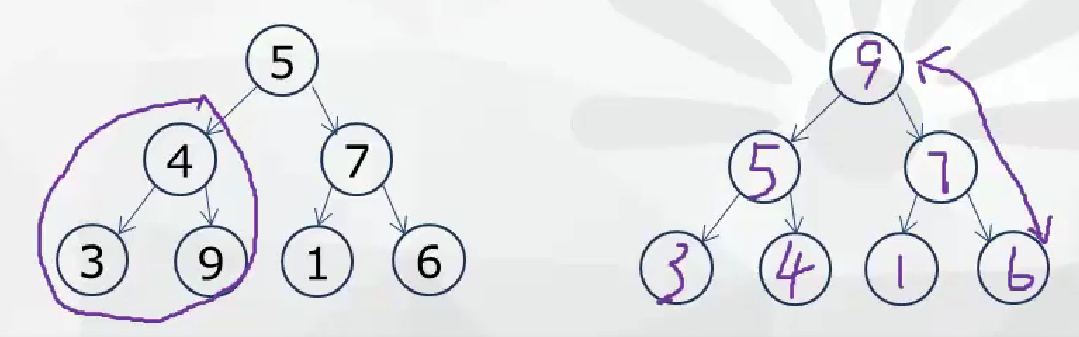
- 堆排序法
最大堆要求节点的元素都要大于其孩子，最小堆要求节点元素都小于其左右孩子，两者对左右孩子的大小关系不做任何要求
保存时从最底下开始从右到左进行交换
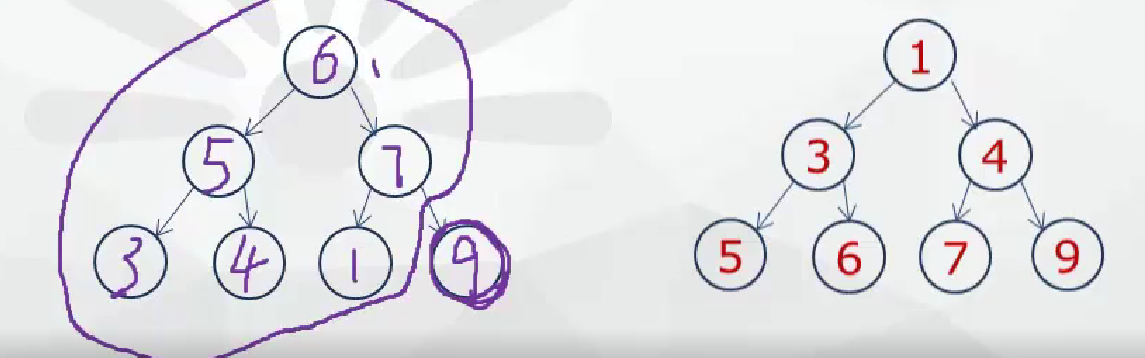
归并排序
将两个或两个以上的有序表组合成一个新的有序表，所需内存最大
比较
求极值
对于长度为n的线性表，要比较n-1次
