数据结构复习（二）

六、特殊矩阵、广义表及其应用

• 行序列序：
  • 以行序为主序存储：对一个具有m行、n列的二维数组A_m*n，线存储第一行，再存储第二行，到m行
  • 以列序为主序存储：对一个具有m行、n列的二维数组A_m*n，线存储第一列，再存储第二列，到m列

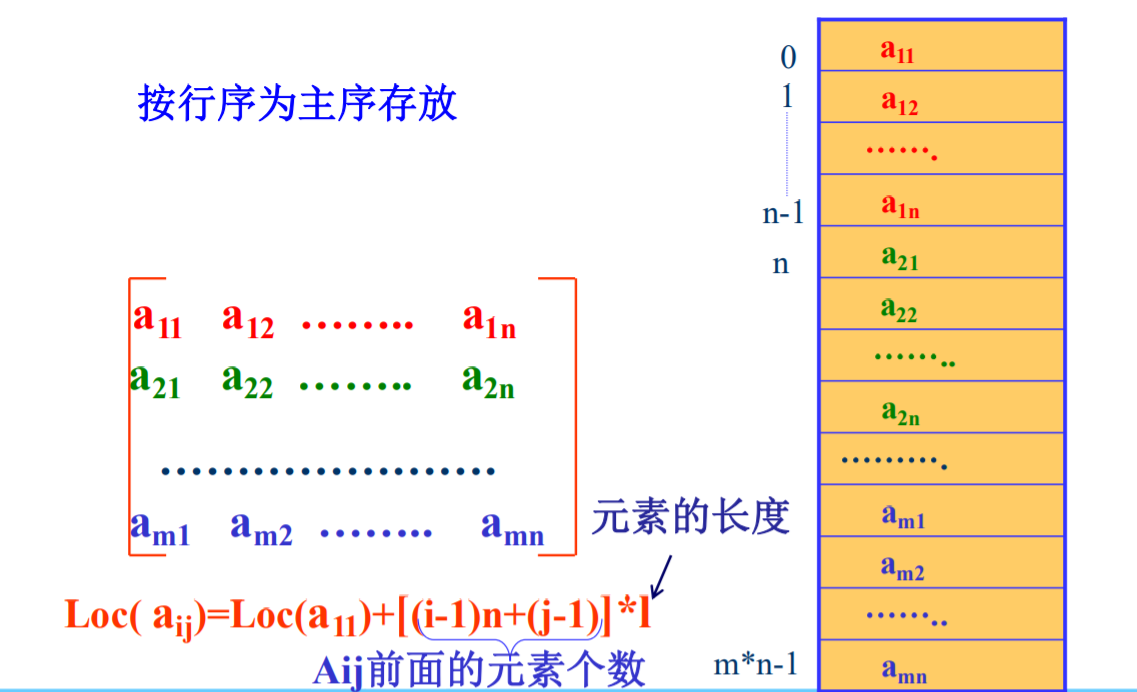
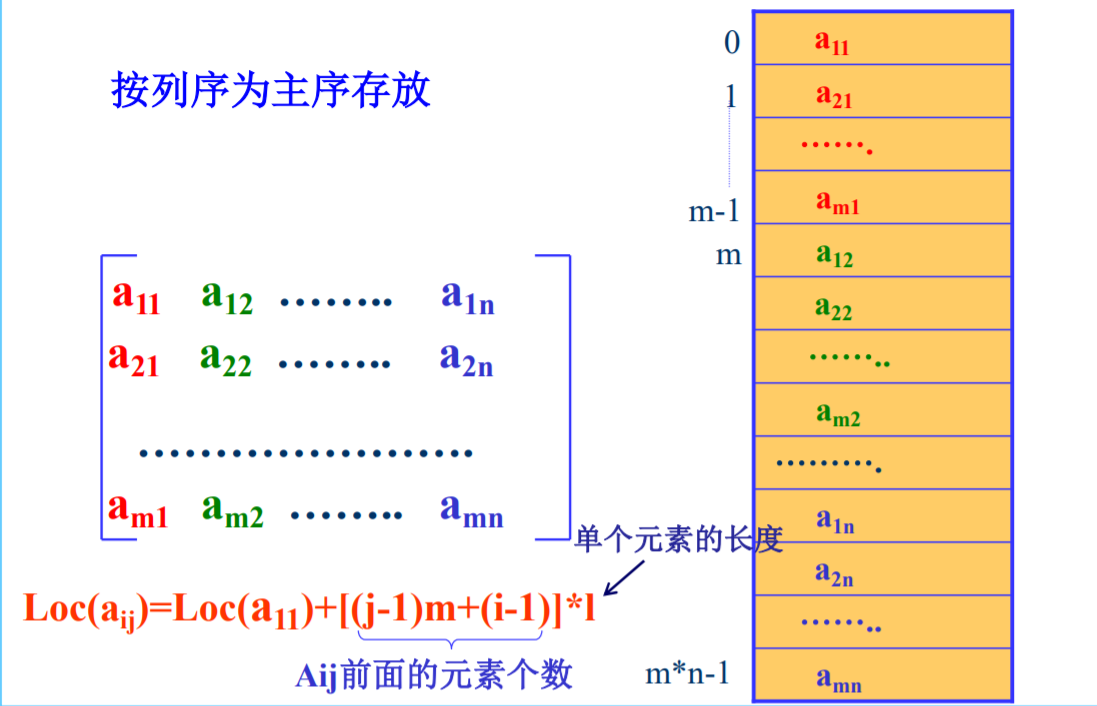
• 映射关系：对称矩阵A_ij=A_ji、i>=j位于下三角，k=i*(i+1)/2+j；i<j上三角k=j*(j+1)/2+i；

　　　　　　　　三角矩阵：上三角，下三角，有常数C

　　　　　　　　对角矩阵：非0元素集中再以主对角线为中心的带状区域

• 转换成下标：对称矩阵一共有元素n(n+1)/2个，用一维数组sa[n(n+1)/2]来存储

　　　　　　　　　三角矩阵：sa[n(n+1)/2+1]，

　　　　　　　　　对角矩阵：3n-2个非0元素，非0时，i=0,j=0,1||0<i<n-1,j=i-1,i,i+1||i=n-1,j=n-2,n-1;

• 画三元组表:（行号，列号，值），非0元素
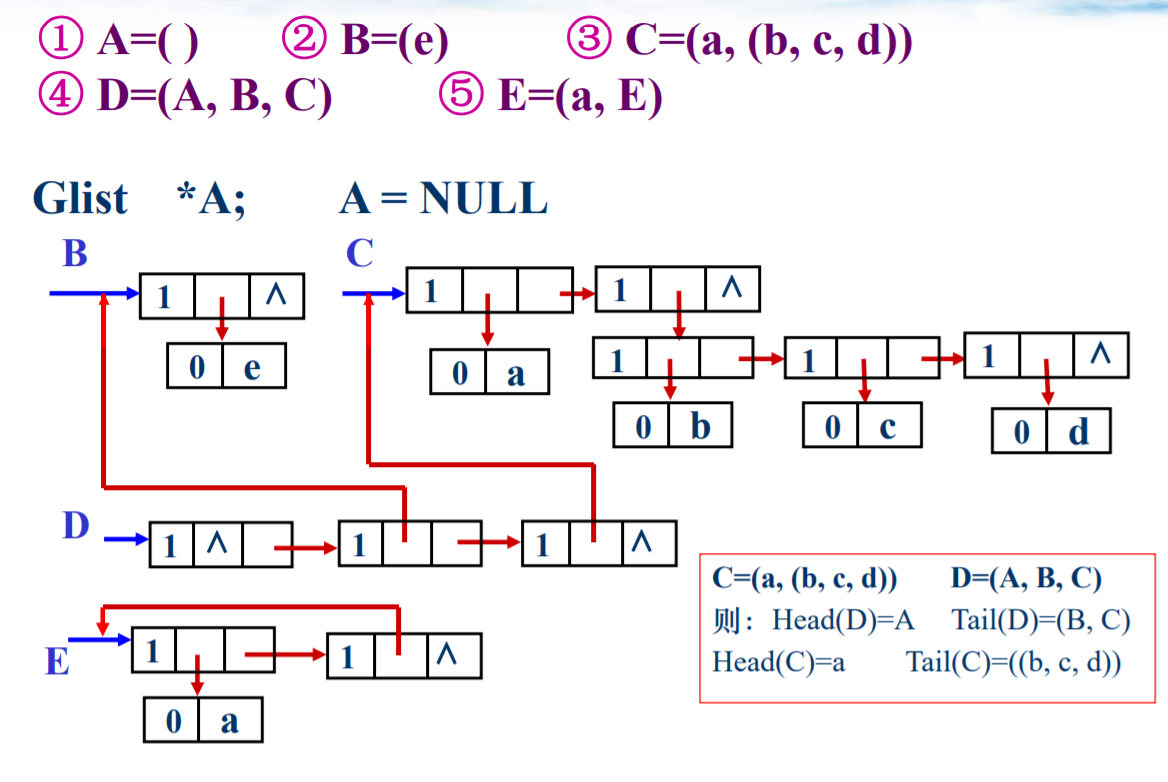
• 广义表表头、表尾写出来：tag=1表结点，tag=0原子结点。

 

 

 

七、二叉树及其应用

• 性质掌握：

1. 在二叉树的第i层最多有2^i-1个结点
2. 深度为k的二叉树至多有2^k-1个结点
3. 对于任一棵非空二叉树，如果其叶子数为n，度为2的结点为m，则n=m+1。

• 满二叉树：任一非叶子结点均有两个孩子，对于二叉树的任一层，若该层上有一个结点有孩子，则该层上所以结点均有孩子。
• 完全二叉树：在满二叉树的最下层从右到左连续的删除若干个结点所得到的二叉树。
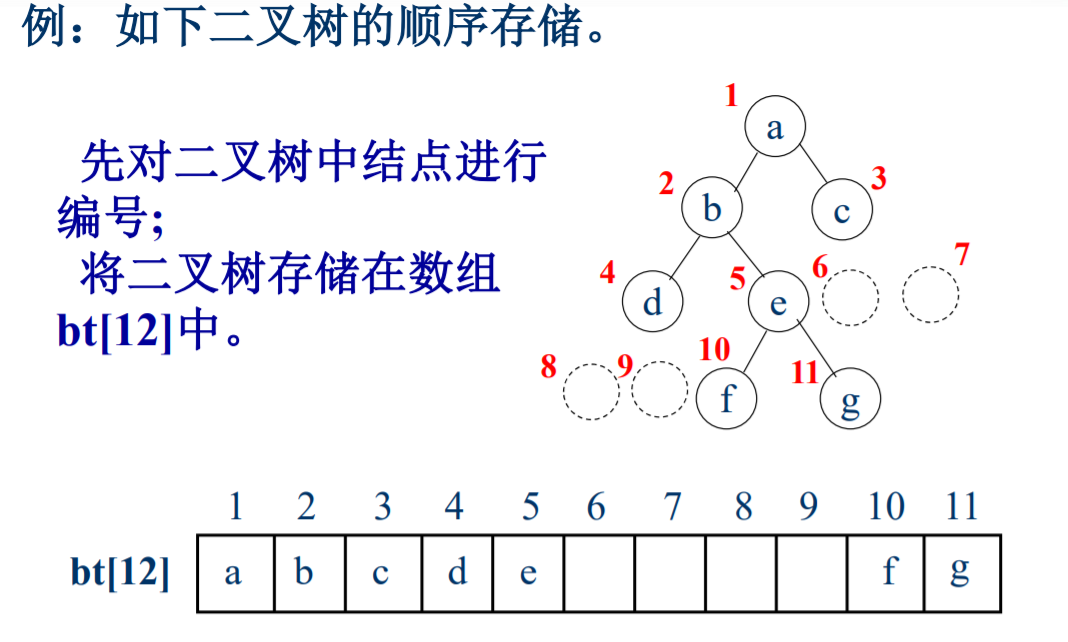
• 二叉树的存储结构画出来：

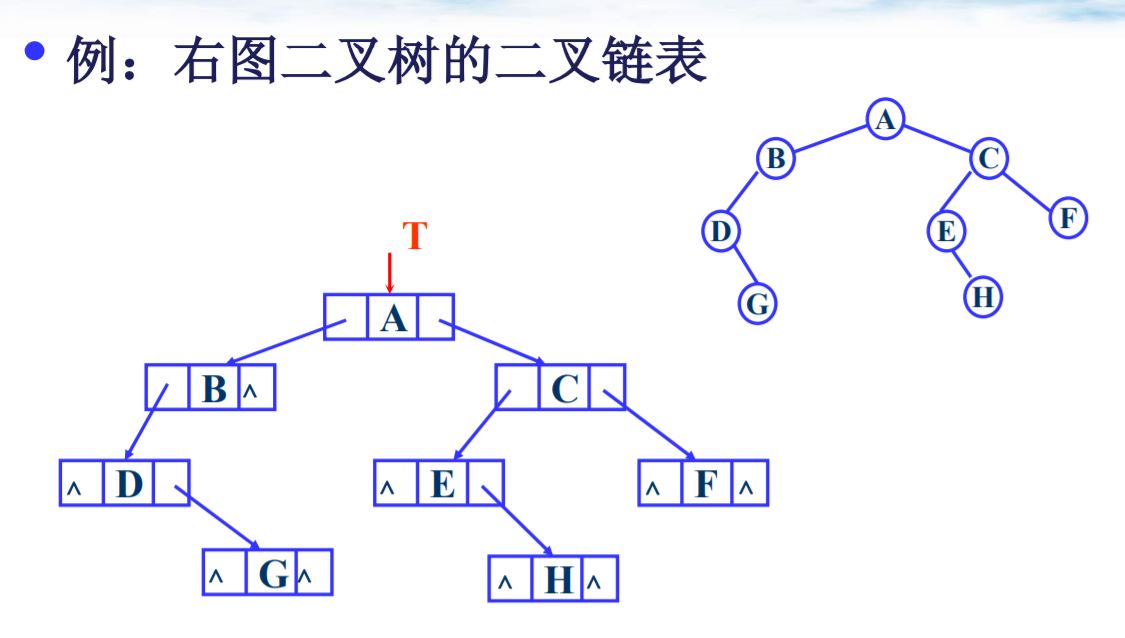
• 二叉链表掌握：
• 建立二叉树的算法代码：

1. 1. 依次输入结点信息，若结点不是虚结点则建立一个新结点
   2. 若新结点时第一个，则为根节点否则新结点作为孩子结点链接到其父节点（设置队列正确的链接到其父结点）
   3. 重复1，2直到输入0位置。

Bitree* Creat()
{
    int ch, front, rear;
    Bitree* T, * S;
    T = NULL;    //置空二叉树
    front = 1; rear = 0;    //置空队列
    scanf_s("%d", &ch);
    while (ch != 0)
    {
        S = NULL;　　//如果时虚结点则s为空
        if (ch != 9)    //不是虚结点时建立新结点
        {
            S = (Bitree*)malloc(sizeof(Bitree));
            S->data = ch;
            S->lchild = S->rchild = NULL;
        }
        rear++;
        Q[rear] = S;    //入队
        if (rear == 1)    //根
            T = S;
        else
        {
            if (S != NULL && Q[front] != NULL)    //孩子和双亲均不是虚结点
                if (rear % 2 == 0) Q[front]->lchild = S;
                else Q[front]->rchild = S;
            if (rear % 2 == 1) front++;    //结点Q[front]的两个孩子以及处理完，front+1
        }
        scanf_s("%d", &ch);
    }
    return T;
}

• 二叉树的遍历代码（递归、非递归先序）;

void preorder(Bitree* T)　　//先序
{
    if (T)
    {
        visite(T);
        preorder(T->lchild);
        preorder(T->rchild);
    }
    else return;
}

　　非递归先序：

void preorder(Bitree* T)
{
    SqStack* S;
    InitStack(S);　　//置空栈
    Bitree* p;　　//定义一个树
    p = T;
    while (p != NULL||!Empty(S))　　//如果树不空或栈也不空
    {
        if (p != NULL)　　//p不空就入栈，找到其左孩子
        {
            visit(p->data);
            Push(S, p);
            p = p->lchild;
        }
        else　　　　//出栈找到其右孩子
        {
            p = Pop(S);
            p = p->rchild;
        }
    }
}

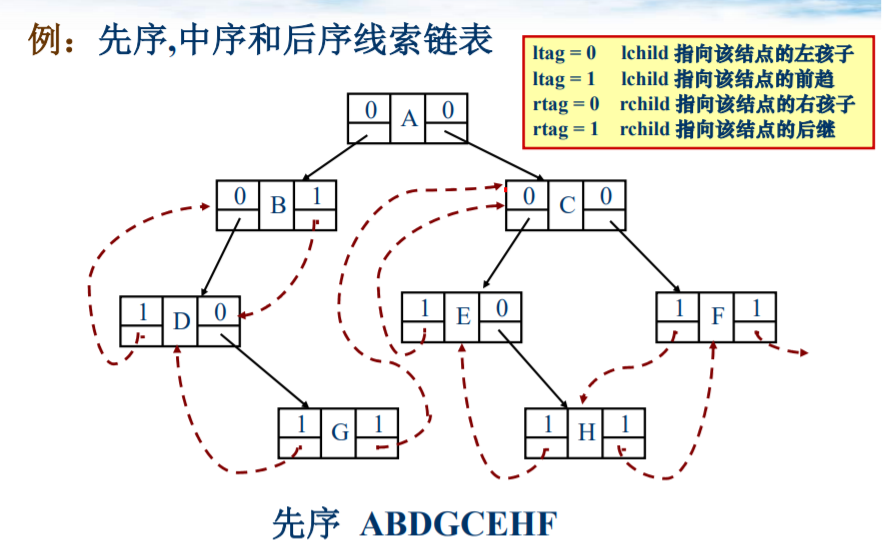
• 线索二叉树会画：将空的左孩子指针域指向前驱，空的右孩子指向其后继。

• 画哈夫曼树：
• 哈夫曼树建树代码：

Huffman(hufmtree tree[])
{
    int i, j, p1, p2;
    float small1, small2;
    for (i = 0; i < n; i++)    //初始化数组
    {
        tree[i].parent = 0;
        tree[i].weight = 0;
        tree[i].lchild = 0;
        tree[i].rchild = 0;
    }
    for (i = 0; i < n; i++)    //读入前n个结点的权值
        scanf_s("%f", &tree[i].weight);
    for (i = n; i < m; i++)    //进行n-1次合并，产生n-1个新结点
    {
        p1 = p2 = 0;
        small1 = small2 = max;
        for (j = 0; j < n; j++)
        {
            if (tree[j].parent == 0)    //选出两个权值最小的根节点
            {
                if (tree[j].weight < small1)    //查找最小下标p1记录
                {
                    small2 = small1;
                    small1 = tree[j].weight;
                    p2 = p1;
                    p1 = j;
                }
                else if(tree[j].weight<small2)    //次小p2记录
                    {
                        small2 = tree[j].weight;
                        p2 = j;
                    }
            }
            tree[p1].parent = tree[p2].parent = i;
            tree[i].weight = tree[p1].weight + tree[p2].weight;
            tree[i].lchild = p1;
            tree[i].rchild = p2;
        }
    }
}

 

• 二叉排序树，序列画出二叉排序树平均查找长度：

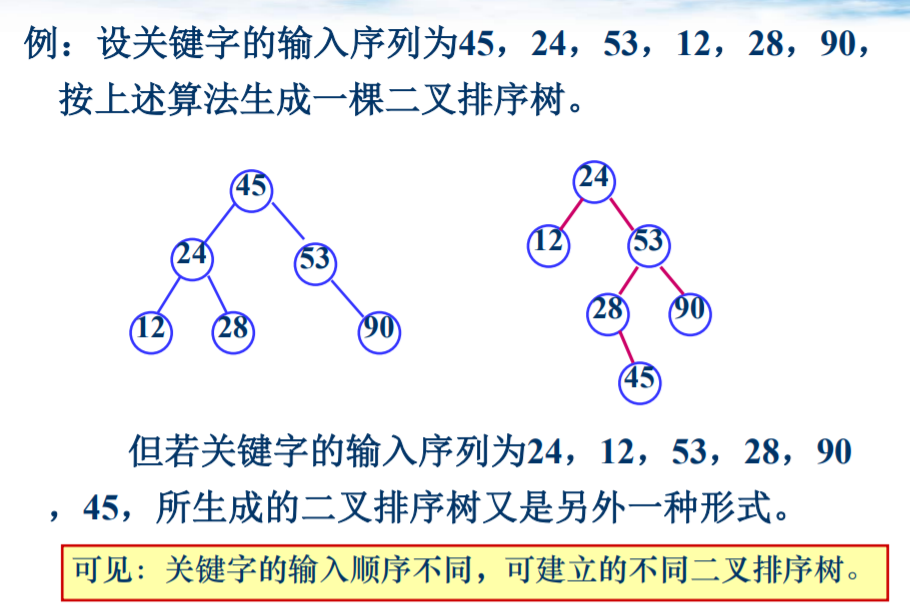
　　平均查找长度：O(log₂n)。

 

八、树和森林及其应用

• 树、森林、二叉树相互转化：
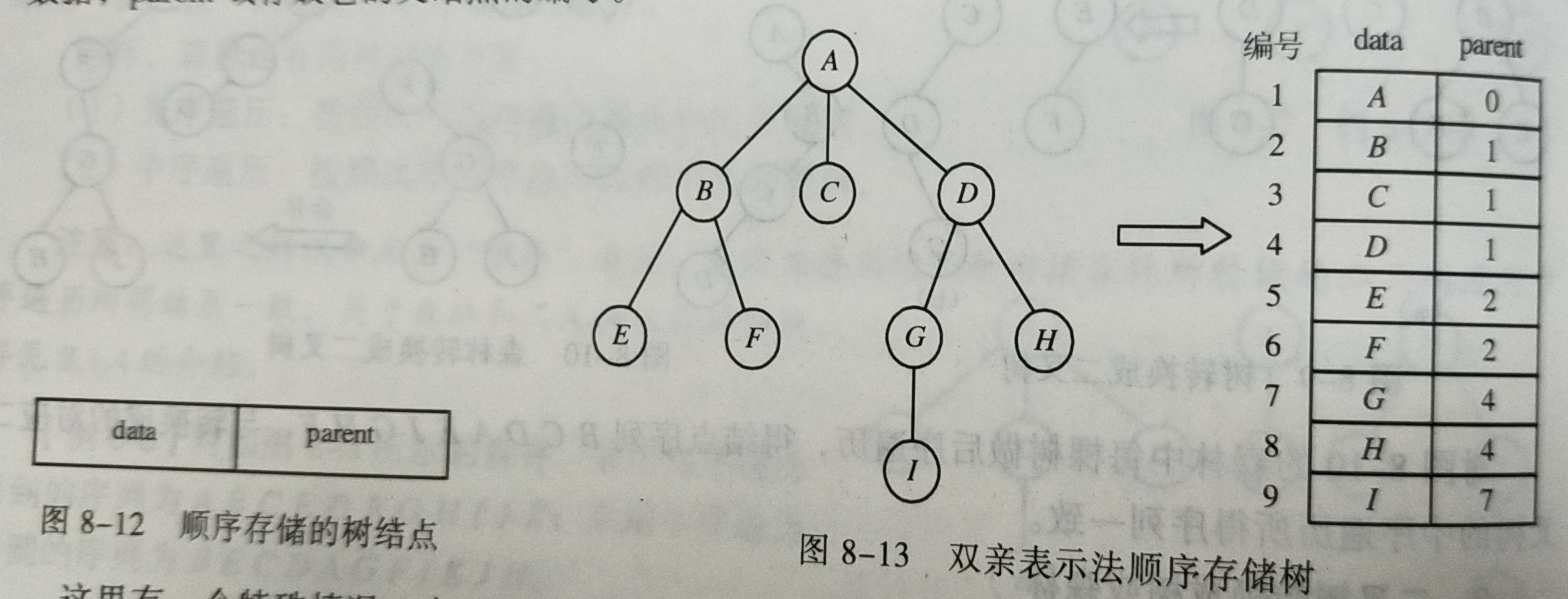
• 树的顺序存储结构和建树算法遍历：
  • 双亲、孩子、孩子兄弟表示法、画图：

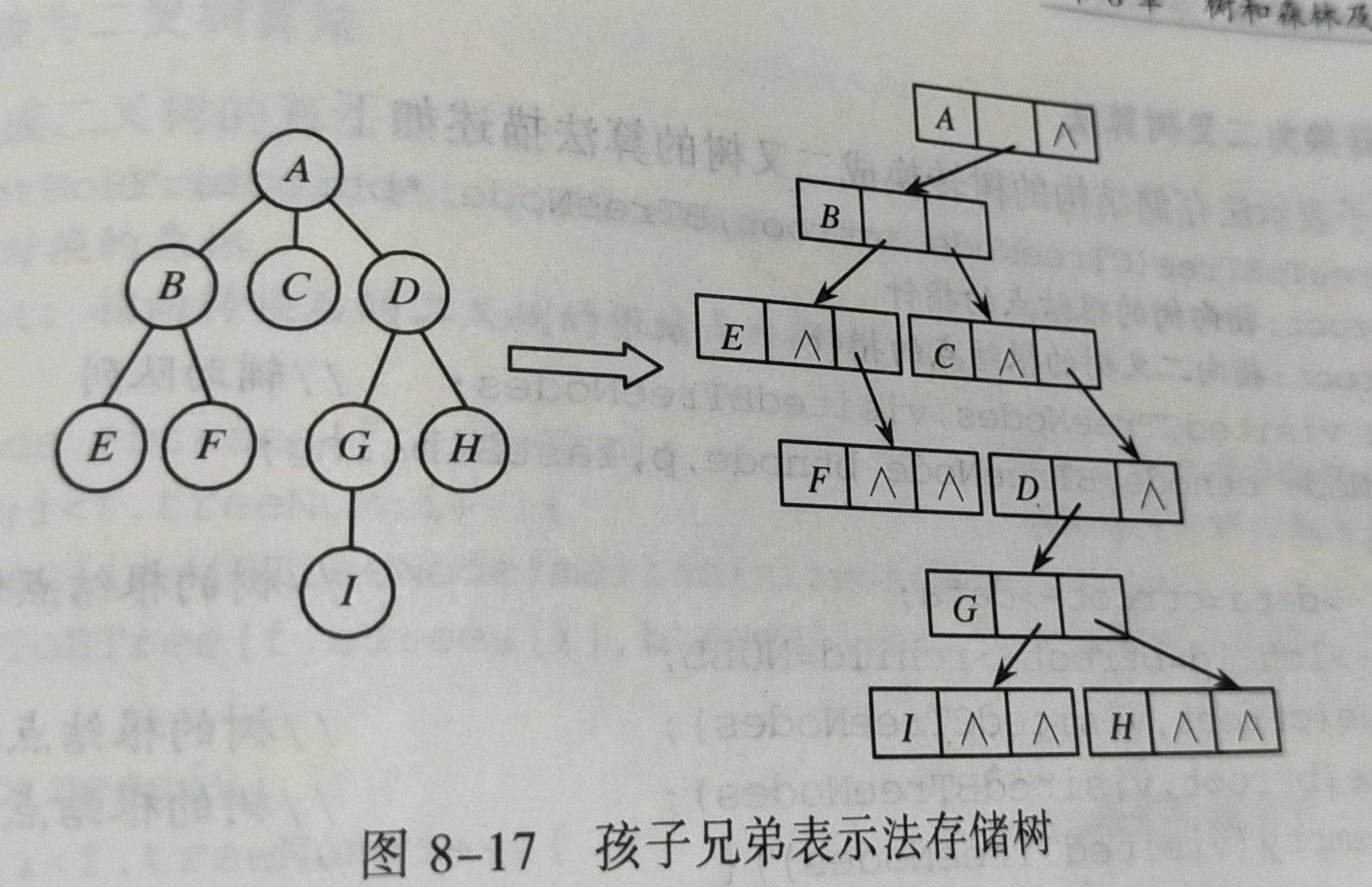
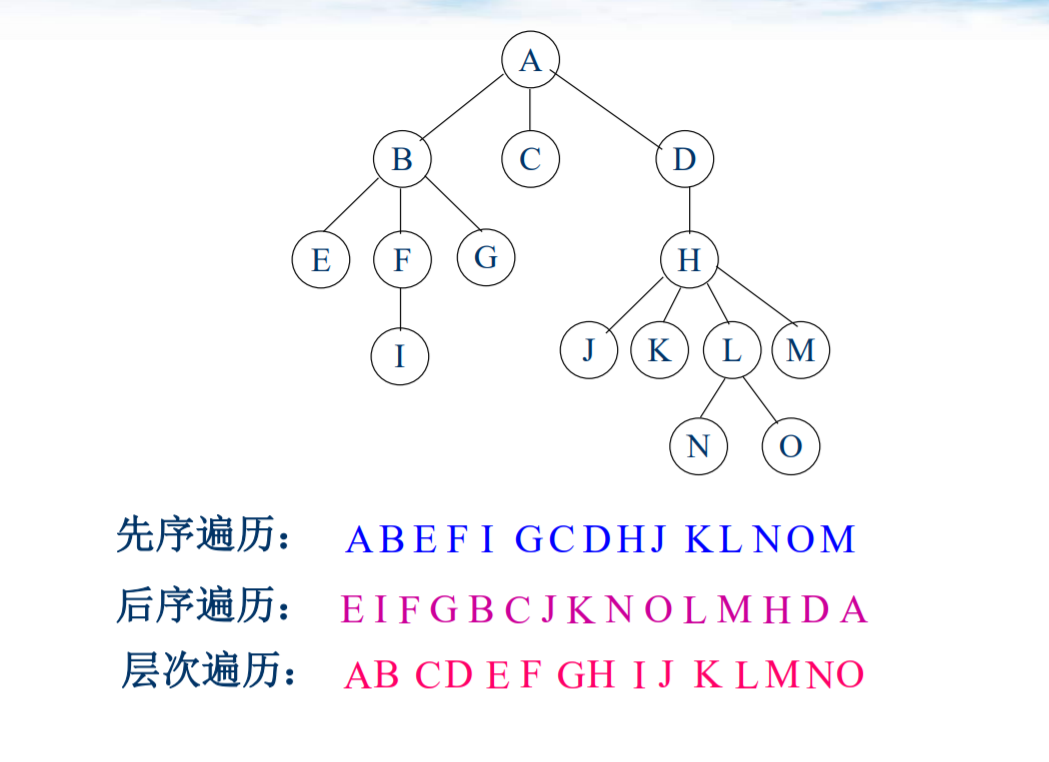
• 树的遍历算法次序写出来：

1. 先序遍历算法：先遍历根，依次先序遍历孩子结点。
2. 后序遍历算法：先依次后序遍历孩子结点，最后遍历根结点。

 

九、散列结构及其应用

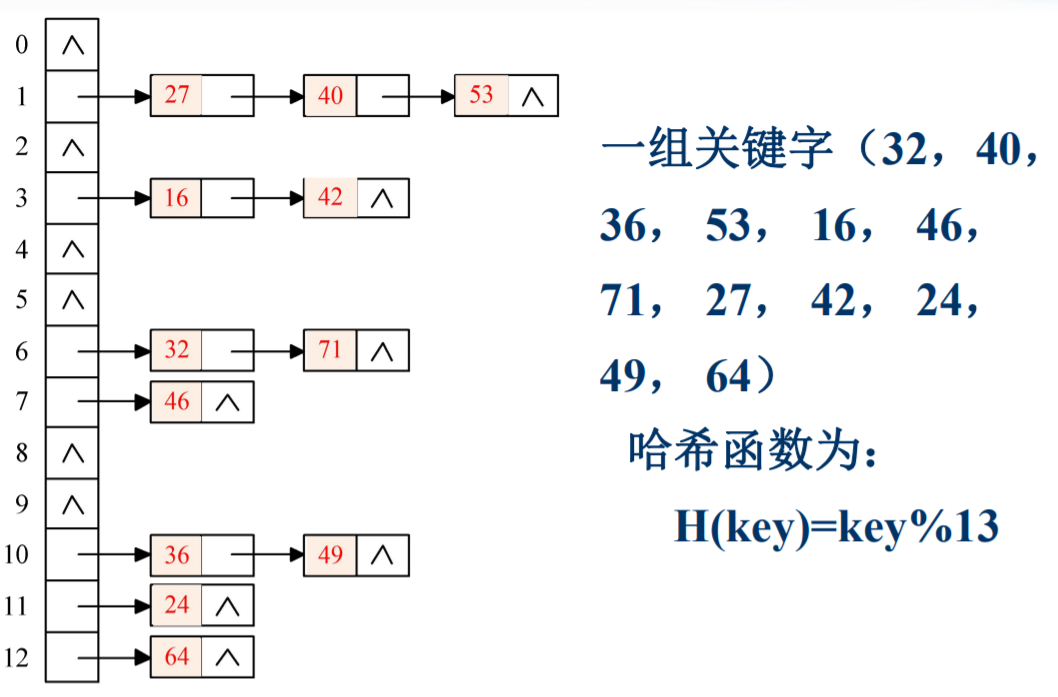
• 存储结构图：
解决冲突的两种方法
• 开放地址法：当关键字冲突，找到一个不冲突的，依次往下找。
• 链地址法：

• 散列结构的查找性能分析插入代码，线性:

      

       

 

 

十、图及其应用

• 邻接矩阵建图代码:

#define Max 10
typedef struct
{
    int num;    //序号
    char data;    //顶点信息
}Vertex;
typedef struct
{
    int n;    //顶点数
    int e;    //边数
    Vertex vex[Max];
    int edgs[Max][Max];
}MGraph;
MGraph* creat_graph()
{
    int i, j, k, w, n, e;
    char c;
    MGraph* mg;
    scanf_s("%d", &n);
    scanf_s("%d", &e);
    mg->n = n;
    mg->e = e;
    getchar();
    printf("输入顶点信息");
    for (i = 0; i < n; i++)
    {
        scanf_s("%d", &c);
        mg->vex[i].data = c;
        mg->vex[i].num = i;
    }
    for (i = 0; i < n; i++)
        for (j = 0; j < n; j++)
            mg->edgs[i][j] = 0;    //把边置空
    printf("输入弧信息");
    for (i = 0; i < e; i++)
    {
        scanf_s("%d%d%d", &j, &k, &w);
        mg->edgs[j][k] = w;
    }
    return mg;
}

• 邻接表:

 

• 深度优先搜索遍历

1. 1. 首先访问某一个指定顶点v0
   2. 从v0出发，访问一个与该点邻接但是没有访问过的点v1
   3. 在从v1出发，选取没有访问过的邻接点v2
   4. 重复3，直到某一个顶点vi的邻接点全部被访问完，后退一步查找前一个顶点vi-1的邻接点
   5. 如果存在未访问的则重复2~4直到所有的点都被访问完

• 广度优先搜索遍历代码

1. 1. 首先访问某一个指定顶点，这是第一层
   2. 然后访问这个点的所以邻接点这是第二层
   3. 以此类推直到所以点被访问完

• 最小生成树画图

1. 1. 普利姆算法：任取顶点选取一条权值最小的边，从顶点出发。
   2. 克鲁斯卡尔算法：从边出发，选取最小的边

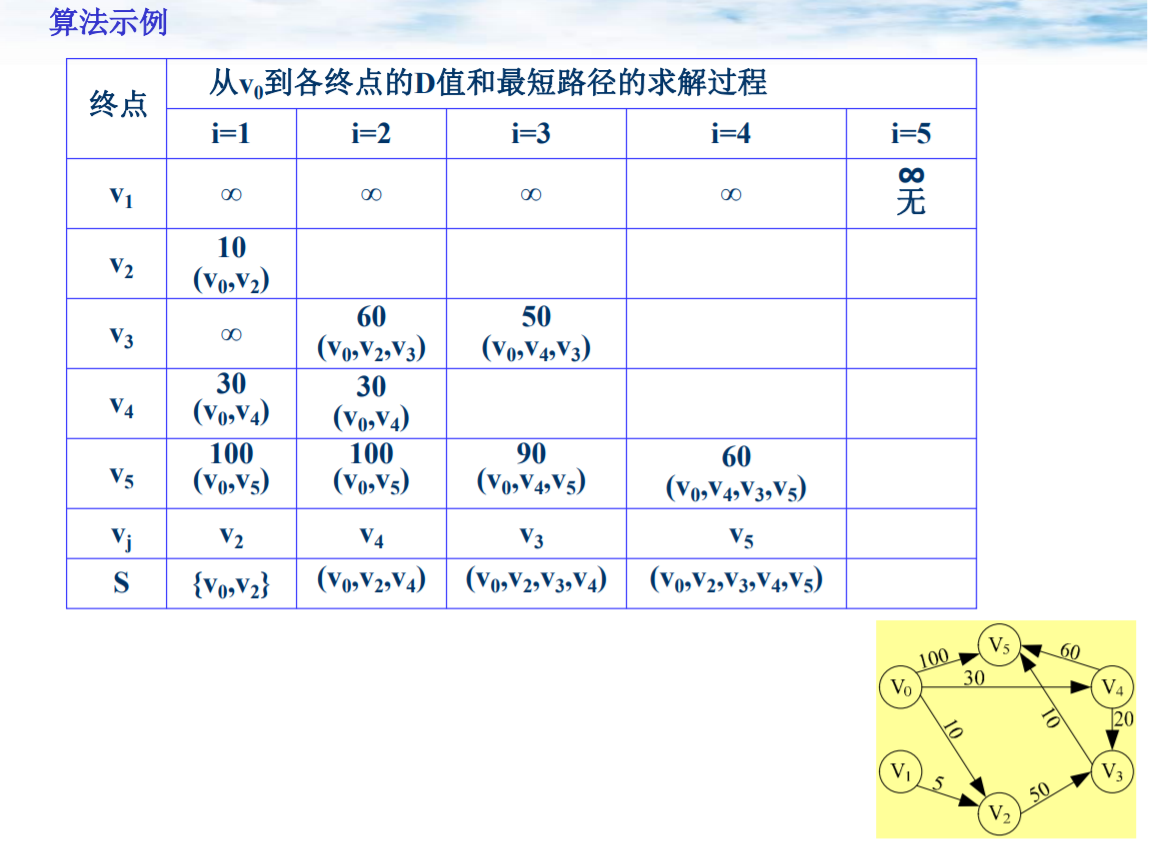
• 最短路径：

• 拓扑排序序列：有向无环图