算法_最小生成树
一.概述
加权无向图是一种在无向图的基础上,为每条边关联一个权值或是成本的图模型.应用可以有很多:例如在一幅航空图中,边表示导线,权值则表示导线的长度或是成本等.
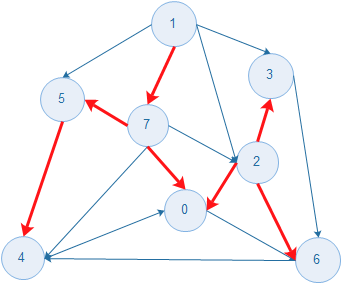
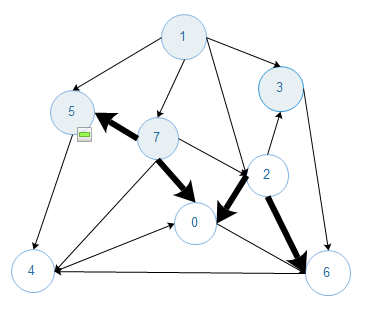
图的生成树是它的一颗含有其所有顶点的无环连通子图,一幅加权图的最小生成树(MST)是它的一颗权值(树中的所有边的权值之和)最小的生成树.下图为一幅加权无向图和它的最小生成树.(箭头不指示方向,标红的为最小生成树).
二.原理
1.图的一种切分是将图的所有顶点分为两个非空且不重叠的两个集合.横切边是连接两个属于不同集合的顶点的边.
2.切分定理:在一幅加权图中,给定任意的切分,它的横切边中的权重最小者必然属于最小生成树.(假设命题不成立,假设权重最小的边为e,将它加入最小生成树必然就会成环,那么这个环应该还有另一条横切边,而该横切边f必然权重>e,那么就可以删除f,得到e,来获取权重更小的生成树.就和最小生成树矛盾,因此命题成立).
三.贪心算法
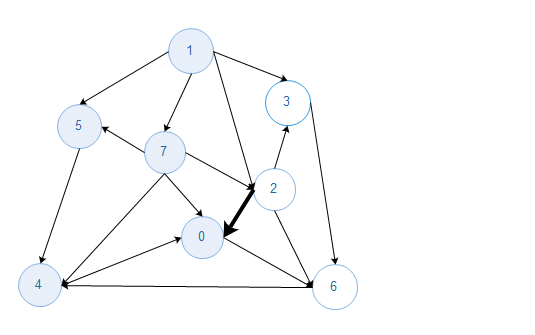
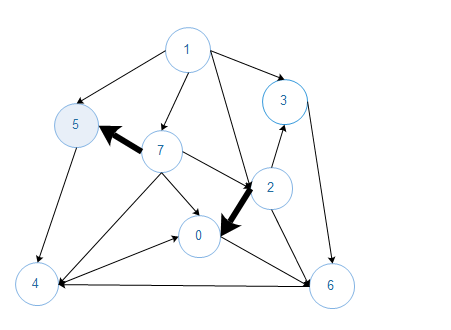
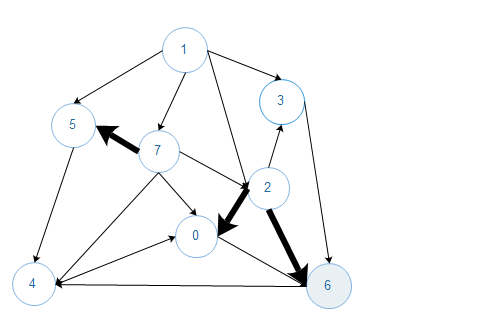
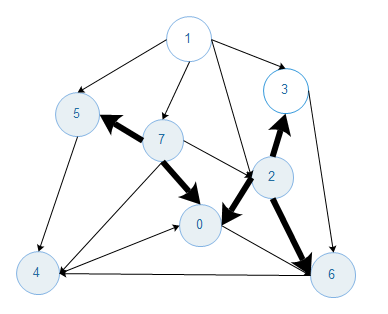
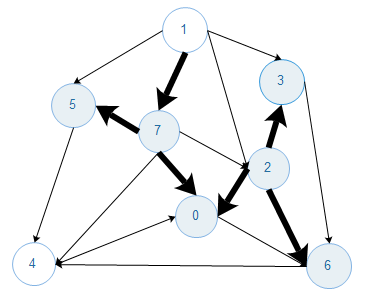
初始状态下,一个含有V个顶点的无向图所有的边都不为黑色,找到一种切分,它所产生的横切边均不为黑色,横切边中权值最小的边标记为黑色(放入最小生成树),如此往复,直到标记了V-1条边.(根据切分定理很容易证明),图的贪心算法的执行流程如下,箭头不指示方向,黑色加粗的边为最小生成树的边.


四.加权无向图的数据类型表示.
1.带权重的边的数据类型:
边的数据类型记录了边的两点,并且给出了获取边其中的某一点,以及根据某点获取另外一个点的方法.同时也用了一个weight的变量来记录边的权重.边的数据结构如下:
//带权重的边的数据类型 public class Edge implements Comparable<Edge>{ private final int v; //顶点之一 private final int w; //另一个顶点 private final double weight; //权重 public Edge(int v, int w, double weight) { super(); this.v = v; this.w = w; this.weight = weight; } public double weight() { return weight; } public int either() { return v; } public int other(int vertex) { if(vertex==v) return w; else if(vertex==w) return v; else throw new RuntimeException("Inconsisitent edge"); } @Override public int compareTo(Edge that) { if(this.weight<that.weight) return -1; else if(this.weight>that.weight) return 1; else return 0; } public String toString() { return String.format("%d%-d %.2f", v,w,weight); } }
2.加权无向图的数据类型:
这个数据类型和Graph的API基本相似,不同的是,这个API的基础是Edge且添加了一个edges方法.加权无向图的代码如下:
public class EdgeWeightedGraph { private final int V; //顶点总数 private int E; //边的总数 private Bag<Edge> [] adj; //邻接表 public EdgeWeightedGraph(int V) { this.V=V; this.E=0; adj=(Bag<Edge> [])new Bag[V];//和Queue不同,Bag保证无序 for(int v=0;v<V;v++) { adj[v]=new Bag<Edge>(); } } public int V() {return V; } public int E() {return E; } public void addEdge(Edge e) { int v=e.either(); int w=e.other(v); adj[v].add(e); adj[w].add(e); E++; } public Iterable<Edge> adj(int v) { return adj[v]; } public Iterable<Edge> edges() { Bag<Edge> list = new Bag<Edge>(); for (int v = 0; v < V; v++) { int selfLoops = 0; for (Edge e : adj(v)) { if (e.other(v) > v) { list.add(e); } else if (e.other(v) == v) { if (selfLoops % 2 == 0) list.add(e); selfLoops++; } } } return list; } }
五.Prim算法
Prim算法为计算最小生成树提供了实现.它的每一步都为树添加一条边.每一次都将下一条连接树中的顶点和不在树中的顶点且权重最小的边加入树中.代码如下所示:
//最小生成树的延迟Prim算法 /** * 先对树上的第0个点进行标记. * 然后遍历第0个点的所有相邻顶点. * 如果没有被标记的话.那么就把对应的边添加进去MinPQ * 在MinPQ中移除权重最小的(如果两个顶点都被标记的话,那么直接继续) * 没有被标记的话,直接visit,标记,然后添加到MinPQ中 * @author Administrator * */ public class LazyPrimMST { private boolean[] marked; //最小生成树的顶点 private Queue<Edge> mst; //最小生成树的边. private MinPQ<Edge> pq; //横切边(其中包括失效的边) public LazyPrimMST(EdgeWeightedGraph G) { pq=new MinPQ<Edge>(); marked=new boolean[G.V()]; mst=new Queue<Edge>(); visit(G,0); //假设G是连通的 while(!pq.isEmpty()) { Edge e=pq.delMin(); int v=e.either(); int w=e.other(v); if(marked[v]&&marked[w]) continue; //忽略无效边 mst.enqueue(e); //将权重最小的边加入最小生成树 if(!marked[v]) visit(G,v); //标记将点加入到集合 if(!marked[w]) visit(G,w); } } private void visit(EdgeWeightedGraph G, int v) { //标记顶点v并将所有连接v和未被标记的顶点的边加入pq marked[v]=true; for(Edge e:G.adj(v)) { if(!marked[e.other(v)]) pq.insert(e); } } public Iterable<Edge> edges() { return mst; } }
之所以称为延迟算法,这是因为MinPQ中保存了大量的无效边.
六.Prim算法的即时实现
Prim算法的即时实现遵循下面的思路:只会在优先队列中保存每个非树顶点w的一条边.采用索引优先队列,将顶点和边关联起来.该边为将它与树中的顶点连接起来的权重最小的边.
PrimMST类有两个数组edgeTo,distTo,他们具有以下性质:
1.如果顶点v不在树中但至少含有一条边与树相连接,那么edgeTo[v]是与树相连接的权重最小的边,distTo[v]是该边的权重.
2.这类点都存放在索引优先队列中.
该算法的基本步骤是PrimMST会从优先队列中取出一个顶点v,并且检查与它相连的点v-w,如果w被标记过,则失效,如果w不在优先队列中或者v-w权重小于目前已知的最小值edgeTo[w],代码会更新数组,将v-w作为树的最佳选择.代码如下:
/** * 先将0加入最小索引队列中.然后通过对于G.adj(v)进行遍历. * 获得不同的边,观察顶点连接到树的边是否小于distTo保存的数值. * 如果小于的话,那么添加进去.或者修改. * 不小于不变.一个个点进行遍历.不断获得各个点到树的最小的距离. * 然后将距离最小的点加进去 * * @author Administrator * */ public class PrimMST { private Edge[] edgeTo; //距离树最近的边 private double[] distTo; //distTo[w]=edgeTo[w].weight() private boolean[] marked; //如果v在树中则为true private IndexMinPQ<Double> pq; //有效的横切边 public PrimMST(EdgeWeightedGraph G) { edgeTo=new Edge[G.V()]; distTo=new double[G.V()]; marked=new boolean[G.V()]; for(int v=0;v<G.V();v++) { distTo[v]=Double.POSITIVE_INFINITY; } pq=new IndexMinPQ<Double>(G.V()); distTo[0]=0.0; pq.insert(0, 0.0); while(!pq.isEmpty()) { visit(G,pq.delMin());//每次都取出权重最小的边 } } private void visit(EdgeWeightedGraph G, int v) { marked[v]=true; for(Edge e:G.adj(v)) { int w=e.other(v); if(marked[w]) continue; //v-w失效 if(e.weight()<distTo[w]) { edgeTo[w]=e; distTo[w]=e.weight(); if(pq.contains(w)) pq.changeKey(w, distTo[w]); else pq.insert(w, distTo[w]); } } } public Iterable<Edge> edges() { Queue<Edge> mst = new Queue<Edge>(); for (int v = 0; v < edgeTo.length; v++) { Edge e = edgeTo[v]; if (e != null) { mst.enqueue(e); } } return mst; } }
七.Kruskal算法
Kruskal算法的思想按照边的权重顺序从小到大处理它们,然后将边按照从小到大的次序加入到最小生成树中,加入的边不会和已经加入的边构成环,直到树中含有v-1条边为止.原理在于如果加入的边不会和已有的边构成环,那么它就是一个跨越了所有和树顶点相邻的顶点组成的集合以及他们的补集所构成的切分.而这个切分的权重又是最小的,根据切分定理,它一定是最小生成树的一条边.
代码的实现如下所示,代码中用了UF判断是否构成环,并且将一个两个点相连,使之共同构成在同一个连通分量.
/** * 首先将所有的边都加入到MinPQ中. * 然后根据权值从小到大依次加入. * 如果该边已经在最小生成树里,就忽略. * 如果不在,那么就加入进去(union方法).直到mst的size达到v-1 * 原则:如果下一条被加入的边不会和已有的形成环.那么它 * 就相当于是一个切分,而它的权重又是最小的.因此可以加入进去 * @author Administrator * */ public class KruskalMST { private Queue<Edge> mst; public KruskalMST(EdgeWeightedGraph G) { mst=new Queue<Edge>(); MinPQ<Edge> pq=new MinPQ<>(); for(Edge e:G.edges()) { pq.insert(e); } UF uf=new UF(G.V()); while(!pq.isEmpty()&&mst.size()<G.V()-1) { Edge e=pq.delMin(); int v=e.either(); int w=e.other(v); if(uf.connected(v, w)) continue; //处于同一个连通分量中. uf.union(v, w); mst.enqueue(e); } } public Iterable<Edge> edges() { return mst; } }
public class UF { private int[] id; //分量id private int count; //分量数量 public UF(int N) { count=N; id=new int[N]; for(int i=0;i<N;i++) { id[i]=i; } } //连通分量的数量 public int count() { return count; } //如果pq存在于同一个连通分量中,则返回true public boolean connected(int p,int q) { return find(p)==find(q); } //p所在的连通分量标识符 public int find(int p) { // TODO Auto-generated method stub return id[p]; } //在p,q之间建立连接(QuickFind算法) public void union(int p,int q) { //将p和q归并到相同的分量中 int pID=find(p); int qID=find(q); //如果已经在相同的分量中则不采取行动 if(pID==qID) return ; for(int i=0;i<id.length;i++) { if(id[i]==pID) id[i]=qID; } count--; } }



