牛客网多校训练第一场 F - Sum of Maximum(容斥原理 + 拉格朗日插值法)
链接:
https://www.nowcoder.com/acm/contest/139/F
题意:
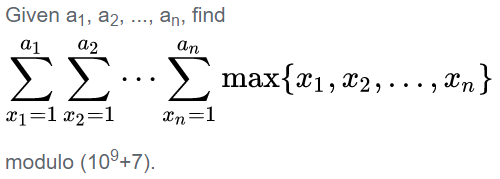

分析:
转载自:http://tokitsukaze.live/2018/07/19/2018niuke1.F/



代码:
1 #include <cstdio> 2 #include <cassert> 3 #include <algorithm> 4 using namespace std; 5 6 /// 注意mod,使用前须调用一次 polysum::init(int M); 7 namespace polysum { 8 #define rep(i,a,n) for (int i=a;i<n;i++) 9 #define per(i,a,n) for (int i=n-1;i>=a;i--) 10 typedef long long ll; 11 const ll mod=1e9+7; /// 取模值 12 ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;} 13 14 const int D=101000; /// 最高次限制 15 ll a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][2],C[D]; 16 ll calcn(int d,ll *a,ll n) { 17 if (n<=d) return a[n]; 18 p1[0]=p2[0]=1; 19 rep(i,0,d+1) { 20 ll t=(n-i+mod)%mod; 21 p1[i+1]=p1[i]*t%mod; 22 } 23 rep(i,0,d+1) { 24 ll t=(n-d+i+mod)%mod; 25 p2[i+1]=p2[i]*t%mod; 26 } 27 ll ans=0; 28 rep(i,0,d+1) { 29 ll t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod; 30 if ((d-i)&1) ans=(ans-t+mod)%mod; 31 else ans=(ans+t)%mod; 32 } 33 return ans; 34 } 35 void init(int M) { /// M:最高次 36 f[0]=f[1]=g[0]=g[1]=1; 37 rep(i,2,M+5) f[i]=f[i-1]*i%mod; 38 g[M+4]=powmod(f[M+4],mod-2); 39 per(i,1,M+4) g[i]=g[i+1]*(i+1)%mod; 40 } 41 ll polysum(ll n,ll *arr,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i] 42 for(int i = 0; i <= m; i++) a[i] = arr[i]; 43 a[m+1]=calcn(m,a,m+1); 44 rep(i,1,m+2) a[i]=(a[i-1]+a[i])%mod; 45 return calcn(m+1,a,n-1); 46 } 47 ll qpolysum(ll R,ll n,ll *a,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i 48 if (R==1) return polysum(n,a,m); 49 a[m+1]=calcn(m,a,m+1); 50 ll r=powmod(R,mod-2),p3=0,p4=0,c,ans; 51 h[0][0]=0;h[0][1]=1; 52 rep(i,1,m+2) { 53 h[i][0]=(h[i-1][0]+a[i-1])*r%mod; 54 h[i][1]=h[i-1][1]*r%mod; 55 } 56 rep(i,0,m+2) { 57 ll t=g[i]*g[m+1-i]%mod; 58 if (i&1) p3=((p3-h[i][0]*t)%mod+mod)%mod,p4=((p4-h[i][1]*t)%mod+mod)%mod; 59 else p3=(p3+h[i][0]*t)%mod,p4=(p4+h[i][1]*t)%mod; 60 } 61 c=powmod(p4,mod-2)*(mod-p3)%mod; 62 rep(i,0,m+2) h[i][0]=(h[i][0]+h[i][1]*c)%mod; 63 rep(i,0,m+2) C[i]=h[i][0]; 64 ans=(calcn(m,C,n)*powmod(R,n)-c)%mod; 65 if (ans<0) ans+=mod; 66 return ans; 67 } 68 } 69 70 typedef long long int LLI; 71 const LLI MOD = polysum::mod; 72 const int UP = 1e3 + 5; 73 LLI a[UP], b[UP]; 74 75 int main() { 76 polysum::init(UP); 77 int n; 78 while(~scanf("%d", &n)) { 79 for(int i = 1; i <= n; i++) scanf("%lld", &a[i]); 80 sort(a+1, a+n+1); 81 LLI ans = 0, prod = 1; 82 for(int i = 1; i <= n; i++) { 83 if(a[i] == a[i-1]) { 84 prod = prod * a[i] % MOD; 85 continue; 86 } 87 for(int x = 1; x <= n-i+1; x++) { 88 b[x] = (polysum::powmod(x, n-i+1) - polysum::powmod(x-1, n-i+1) + MOD) % MOD * x % MOD; 89 } 90 LLI temp = (polysum::polysum(a[i]+1, b, n-i+1) - polysum::polysum(a[i-1]+1, b, n-i+1) + MOD) % MOD; 91 ans = (ans + prod * temp % MOD) % MOD; 92 prod = prod * a[i] % MOD; 93 } 94 printf("%lld\n", ans); 95 } 96 return 0; 97 }
拉格朗日插值法模板(杜教版):
1 /// 注意mod,使用前须调用一次 polysum::init(int M); 2 namespace polysum { 3 #define rep(i,a,n) for (int i=a;i<n;i++) 4 #define per(i,a,n) for (int i=n-1;i>=a;i--) 5 typedef long long ll; 6 const ll mod=1e9+7; /// 取模值 7 ll powmod(ll a,ll b) {ll res=1;a%=mod; assert(b>=0); for(;b;b>>=1){if(b&1)res=res*a%mod;a=a*a%mod;}return res;} 8 9 const int D=101000; /// 最高次限制 10 ll a[D],f[D],g[D],p[D],p1[D],p2[D],b[D],h[D][2],C[D]; 11 ll calcn(int d,ll *a,ll n) { 12 if (n<=d) return a[n]; 13 p1[0]=p2[0]=1; 14 rep(i,0,d+1) { 15 ll t=(n-i+mod)%mod; 16 p1[i+1]=p1[i]*t%mod; 17 } 18 rep(i,0,d+1) { 19 ll t=(n-d+i+mod)%mod; 20 p2[i+1]=p2[i]*t%mod; 21 } 22 ll ans=0; 23 rep(i,0,d+1) { 24 ll t=g[i]*g[d-i]%mod*p1[i]%mod*p2[d-i]%mod*a[i]%mod; 25 if ((d-i)&1) ans=(ans-t+mod)%mod; 26 else ans=(ans+t)%mod; 27 } 28 return ans; 29 } 30 void init(int M) { /// M:最高次 31 f[0]=f[1]=g[0]=g[1]=1; 32 rep(i,2,M+5) f[i]=f[i-1]*i%mod; 33 g[M+4]=powmod(f[M+4],mod-2); 34 per(i,1,M+4) g[i]=g[i+1]*(i+1)%mod; 35 } 36 ll polysum(ll n,ll *arr,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i] 37 for(int i = 0; i <= m; i++) a[i] = arr[i]; 38 a[m+1]=calcn(m,a,m+1); 39 rep(i,1,m+2) a[i]=(a[i-1]+a[i])%mod; 40 return calcn(m+1,a,n-1); 41 } 42 ll qpolysum(ll R,ll n,ll *a,ll m) { // a[0].. a[m] \sum_{i=0}^{n-1} a[i]*R^i 43 if (R==1) return polysum(n,a,m); 44 a[m+1]=calcn(m,a,m+1); 45 ll r=powmod(R,mod-2),p3=0,p4=0,c,ans; 46 h[0][0]=0;h[0][1]=1; 47 rep(i,1,m+2) { 48 h[i][0]=(h[i-1][0]+a[i-1])*r%mod; 49 h[i][1]=h[i-1][1]*r%mod; 50 } 51 rep(i,0,m+2) { 52 ll t=g[i]*g[m+1-i]%mod; 53 if (i&1) p3=((p3-h[i][0]*t)%mod+mod)%mod,p4=((p4-h[i][1]*t)%mod+mod)%mod; 54 else p3=(p3+h[i][0]*t)%mod,p4=(p4+h[i][1]*t)%mod; 55 } 56 c=powmod(p4,mod-2)*(mod-p3)%mod; 57 rep(i,0,m+2) h[i][0]=(h[i][0]+h[i][1]*c)%mod; 58 rep(i,0,m+2) C[i]=h[i][0]; 59 ans=(calcn(m,C,n)*powmod(R,n)-c)%mod; 60 if (ans<0) ans+=mod; 61 return ans; 62 } 63 }



