【题解】洛谷 P4339 [ZJOI2018]迷宫 (UOJ#375)

这篇文章的所有图片使用 \(\operatorname{Graphviz}\) 生成，在此鸣谢。

初稿 on 2020-05-28 16:26:54

构造有 \(K\) 个点的“基本方案”

考虑构造一个有 \(∞\) 个点的方案。
为了方便，我们假设题目中的 \(1\) 号点为 \(0\) 号点。
对于一个点 \(x\)，我们使它的第 \(i(i\in[0,m-1])\) 条出边指向节点 \(x · m + i\)。
为了使得路径能回到 \(0\) 号点，我们使所有满足 \(x\equiv 0 \pmod {K}\) 的点的第 \(0\) 条出边都指向 \(0\)。容易证明这样一定是可行的。
于是我们容易想到，如果把每个节点的编号都模上 \(K\)，我们将得到一个有 \(K\) 个点的方案。

整理一下：
为了得到一个有 \(K\) 个点的方案，对于每一个节点 \(x\in[0,K-1]\)，其第 \(i(i\in[0,m-1])\) 条出边指向节点 \((x · m + i)\bmod K\)。

“缩点”

我们发现，样例中第一组数据是满足我们的构造方案的，但是第二、三组数据的答案均比 \(n=K\) 优秀。
考虑用我们的方案先构造一个 \(m=2,n=K=4\) 的方案

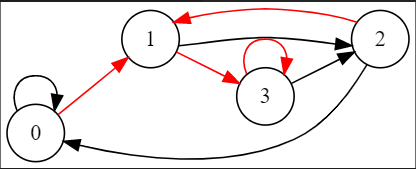
其中黑色边表示 \(0\) 号边，红色边表示 \(1\) 号边。
我们能发现什么东西么？
基本事实 1 如果两个点可以到达的点集相同，那么这两个点可以被缩成 1 个点。
所谓“可以到达的点集相同”，形式化的说，对于两个点 \(a,b\)，是指 \(\forall \ {0\le i<m}\)，有 \((a · m + i)\bmod K = (b · m + i)\bmod K\) 或者 \((a · m + i)\bmod K = b\) 或者 \((b · m + i)\bmod K = a\)
感性理解，就是缩点之后， \(\forall \ {0\le i<m}\), 被缩点的第 \(i\) 条出边指向的目标点不会不同。
如样例第二组数据，可以对 \(1,3\) 号节点缩点，变成这样：

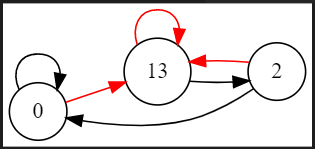
可以发现，这就是样例解释。
（\(0\) 号点对应样例 \(1\) 号点，\(2\) 号点对应样例 \(2\) 号点，\(13\) 号点对应样例 \(3\) 号点）

再给一张大一点的图（对应样例第三组数据）。
黑色边表示 \(0\) 号边，红色边表示 \(1\) 号边，绿色边表示 \(2\) 号边，蓝色边表示 \(3\) 号边，紫色边表示 \(4\) 号边，橙色边表示 \(5\) 号边。

当 \(m=6,K=8\) 时可以构造出一个 \(n=8\) 的基本方案

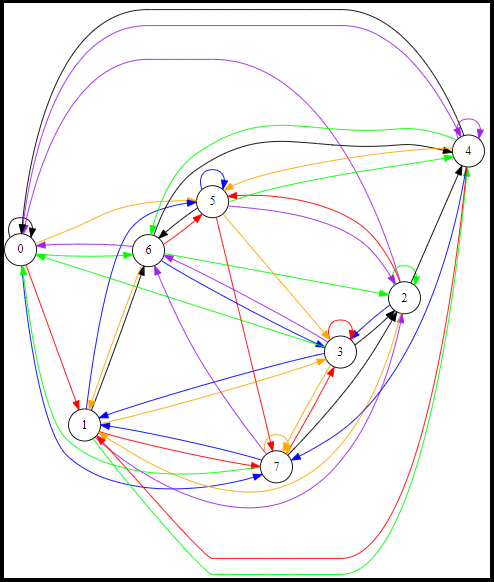
缩点后得到一个 \(n=5\) 的最佳方案

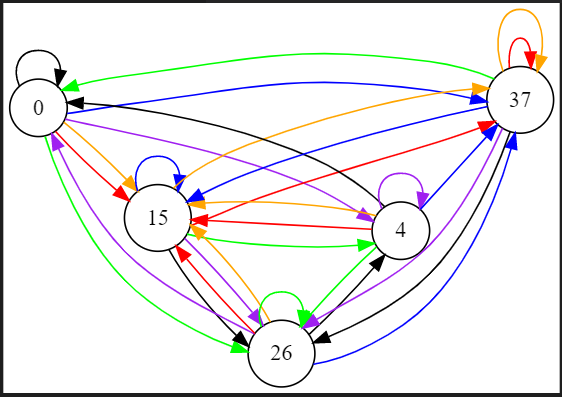
可以手玩一下验证其正确性
即样例输出

关于 \(0\) 号节点

注意到上面几张图中 \(0\) 号节点都没有被缩点。
注意到这个节点比较的特殊，不能被缩点。
为什么？
因为 \(0\) 号节点可以被作为迷宫的结束点，而别的任意一个节点均不满足这一性质，自然不能与 \(0\) 号节点一起缩点。
但是其他与 \(0\) 可以到达的点集相同的点之间时可以缩点的。
口说无凭，以图解释。
\(m=3,K=3\) （黑色边表示 \(0\) 号边，红色边表示 \(1\) 号边，绿色边表示 \(2\) 号边）
基本方案 \(n = 3\)

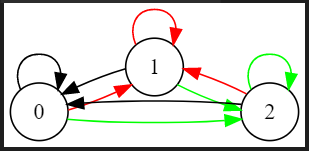
缩点后 \(n = 2\)

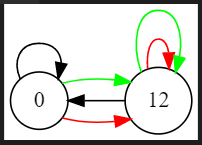
什么时候可以缩点

对于两个可以缩的点 \(a, b\)
因为 \(\forall 0\le i<m,a·m+i\equiv b·m+i\pmod K\)
所以若有 \(a·m\equiv b·m\pmod K\) 则可以缩点
设 \(g = \gcd(m, K)\)
则有 \(a·\frac{m}{g}\equiv b·\frac{m}{g}\pmod {\frac{K}{g}}\)
设 \(m^′=\frac{m}{g},K^′=\frac{K}{g}\)
则有 \(a·m^′\equiv b·m^′\pmod {K^′}\)
此时 \(m^′,K^′\) 互质
那么若有 \(a\not\equiv 0 \pmod {K^′}\) 且 \(b\not\equiv 0 \pmod {K^′}\)，就一定有 \(a\equiv b \pmod {K^′}\)

证明：
不妨设 \(a=cK^′+e,b=dK^′+f\)
其中 \(e,f\in[0,K^′)\) 且 \(c,d,e,f\) 均为自然数
\(\therefore a\equiv e\pmod {K^′},b\equiv f\pmod {K^′}\)
\(\because a·m^′\equiv m^′(cK^′+e)\equiv m^′cK^′+m^′e\equiv m^′e\pmod {K^′},\)
\(b·m^′\equiv m^′(dK^′+f)\equiv m^′dK^′+m^′f\equiv m^′f\pmod {K^′}\)
\(\therefore m^′e=m^′f\pmod {K^′}\)
\(\because m^′,K^′\) 互质且 \(a\not\equiv 0 \pmod {K^′}\)， \(b\not\equiv 0 \pmod {K^′}\)
\(\therefore e=f\)
\(\therefore a\equiv b\pmod {K^′}\)
因此原命题得证

考虑计算哪些点可以缩点。
对于点 \(x\)，\(x\) 可以化为 \(x=yK^′+z\)，其中 \(z\in[0,K^′)\) 且 \(y,z\) 均为自然数。
一个点可以被缩点，当且仅当 \(z\not ={0}\)。
此时能与点 \(x\) 缩为一点的点 \(z\) 都相等。
而对于 \(x\in [0,K)\)，\(z\) 相等的数有 \(g\) 个。
因此，对于同一个 \(z\) 对应的 \(g\) 个点，缩为一点的时候会减少 \(g-1\) 个点。
因为 \(z\in [1,K^′)\) 时可以缩点，所以有 \(K^′-1\) 组可以缩的点，这些点会使答案减少 \((g-1)(K^′-1)\)
所以最终答案为 \(K - (g-1)(K^′-1)\)，其中 \(g = \gcd(m, K)\)

发现这一性质满足样例的三组数据。
提交后，我们获得了 \(0\) 分的好成绩。

论证之不严密

我们发现，有些点是可以被二次缩点的。
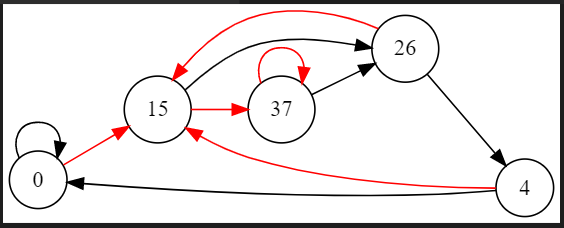
观察下列 \(m=2,K=8\) 的图（黑色边表示 \(0\) 号边，红色边表示 \(1\) 号边）
基本方案 \(n=8\)

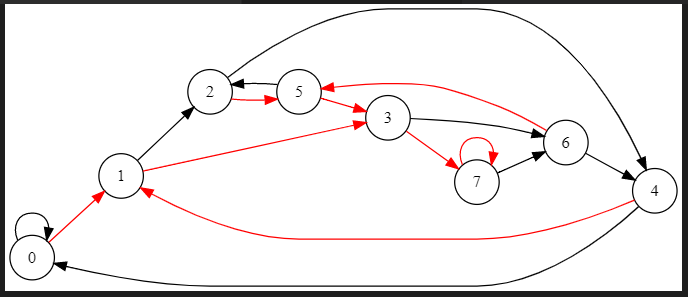
一次缩点 \(n=6\)

二次缩点 \(n=5\)

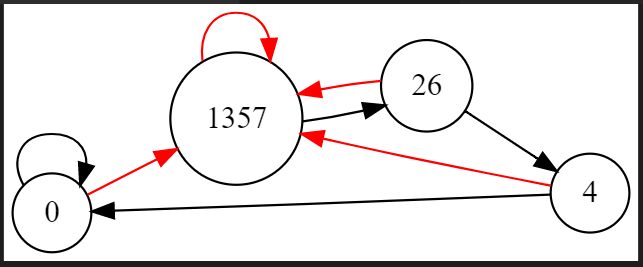
这时候我们的原计算方案就失效了，需要寻求新的解决方案。

递归缩点

由于需要多次缩点，考虑递归求解。

发现两个点 \(x,y\) 能被二次缩点，一定需要满足 \(x·m^u=y·m^u \pmod{K^′}\)
不妨设当前缩点后还剩下 \(r\) 个点，不妨设其编号为 \(1\dots r\) （排除 \(0\) 号节点）。
需要注意，在前一轮缩点中没有被缩点的点，下一轮一定不可能被缩点（自行感性理解，或者结合上面 \(m=2,K=8\) 的图理解，不会证）
考虑设计一个函数 solve，返回缩点中去除了几个节点。
分析这个函数需要的参数。
由于每次一定进行了缩点，\(r\) 值变化, \(r\) 需要作为参数。
同时需要参数 \(t=m^u\) （其中 \(u\) 的实际意义是递归次数，但不会存储）
还需要参数 \(K\)。因为每次计算时都使用 \(K^′\)，所以应该将 \(K^′\) 传给下一层递归函数。
同时由于我们下传的 \(K\) 每次都除以了 \(g\)，下传的 \(t\) 也应该一并除以 \(g\) （实际原因：\(t\) 实际不是 \(u\) 次递归中 \(m\) 的乘积，而应该是 \(u\) 次递归中 \(m^′\) 的乘积）
考虑到如果 \(g=1\)，那么一定不能缩点（显然不证）
考虑到如果 \(r<K^′\)，点的个数小于“出边构成的集合”的种类数，也不能缩点。
因此上述两种情况都应该返回 \(0\) 以表示缩去了 \(0\) 个点。
考虑到缩点的时候，缩得的 \(K^′\) 个点中有 \(t\) 个点是不可能再次被缩的，因此传给下一层 solve 的 \(r\) 应为 \(K^′-t\)

考虑递归终止条件。
假设 \(r<0\) 显然应该终止。
但是 如果这样计算，\(t\) 有可能会爆 int64（实测 \(80\) \(pts\)），所以我们需要再上一层就判断传给下一层的 \(r\) 的正负，而且不应当用整数乘法，应当用浮点数除法
（事实上，你可以使用 __int128 解决问题，但不能保证 ZJOI i3 老年机会不会返回 \(0\) 分的好成绩）

solve 的返回值应为下一层递归的结果加上 \(r-K^′\)（到这一层剩余的点减去缩得的点个数）

代码放 solve 函数和 main 函数

其中 K_ 表示 \(K^′\)，m_ 表示 \(m^′\)

typedef long long int64;

int64 solve(int64 r, int64 t, int64 K) {
    int64 g = gcd(m, K), K_ = K / g, m_ = m / g;
    if (g == 1 || r <= K_) return 0;
    if ((double)K_ / m_ < t) return r - K_;
    t *= m_;
    return solve(K_ - t, t, K_) + r - K_;
} 
int main()
{
    T = read<int>();
    while (T--) {
        m = read<int64>();
        K = read<int64>();
        int64 g = gcd(m, K), K_ = K / g;
        write(K - solve(K - 1, 1, K), 10);
    }
    return 0;
}