洛谷 题解 P1600 【天天爱跑步】 (NOIP2016)
必须得说,这是一道难题(尤其对于我这样普及组205分的蒟蒻)
提交结果(NOIP2016 天天爱跑步):
| OJ名 | 编号 | 题目 | 状态 | 分数 | 总时间 | 内存 | 代码 / 答案文件 | 提交者 | 提交时间 |
|---|---|---|---|---|---|---|---|---|---|
| LibreOJ | #141034 | #2359. 「NOIP2016」天天爱跑步 | Accepted | 100 | 2454 ms | 72492 KiB | C++ / 6.3 K | hkxadpall | 2018-07-28 16:12:23 |
| Vijos | 5b5c3486d3d8a169f1b83bb0 | P2004 天天爱跑步 | Accepted | 100 | 5445ms | 102.0 MiB | C++ / 5.85KB | 航空信奥 LV 8 | 2018-07-28 17:16:54 |
| 洛谷 | R9012867 | P1600 天天爱跑步 | Accepted | 100 | 3712 ms | 102.2MB | C++ / 5.85KB | 航空信奥 | 2018-07-28 16:13:03 |
题面(by 洛谷)
题目描述
小c同学认为跑步非常有趣,于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏,需要玩家每天按时上线,完成打卡任务。
这个游戏的地图可以看作一一棵包含 n 个结点和 n-1 条边的树, 每条边连接两个结点,且任意两个结点存在一条路径互相可达。树上结点编号为从 1 到 n 的连续正整数。
现在有 m 个玩家,第 i 个玩家的起点为 Si ,终点为 Ti 。每天打卡任务开始时,所有玩家在第 0 秒同时从自己的起点出发, 以每秒跑一条边的速度, 不间断地沿着最短路径向着自己的终点跑去, 跑到终点后该玩家就算完成了打卡任务。 (由于地图是一棵树, 所以每个人的路径是唯一的)
小c想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点 j 的观察员会选择在第 Wj 秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第 Wj 秒也理到达了结点 j 。 小C想知道每个观察员会观察到多少人?
注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点 j 作为终点的玩家: 若他在第 Wj 秒前到达终点,则在结点 j 的观察员不能观察到该玩家;若他正好在第 Wj 秒到达终点,则在结点 j 的观察员可以观察到这个玩家。
输入输出格式
输入格式:
第一行有两个整数 n 和m 。其中 n 代表树的结点数量, 同时也是观察员的数量,m 代表玩家的数量。
接下来 n- 1 行每行两个整数 u 和 v ,表示结点 u 到结点 v 有一条边。
接下来一行 n 个整数,其中第 j 个整数为 Wj, 表示结点 j 出现观察员的时间。
接下来 m 行,每行两个整数 Si ,和 Ti ,表示一个玩家的起点和终点。
对于所有的数据,保证1≤Si,Ti≤n,0≤Wj≤n 。
输出格式:
输出1行 n 个整数,第 j 个整数表示结点 j 的观察员可以观察到多少人。
输入输出样例
5 3 1 2 2 3 2 4 1 5 0 1 0 3 0 3 1 1 4 5 5
1 2 1 0 1
说明
【样例1说明】
对于 1 号点, Wi=0 ,故只有起点为1号点的玩家才会被观察到,所以玩家 1 和玩家 2 被观察到,共有 2人被观察到。
对于 2 号点,没有玩家在第 2 秒时在此结点,共 0 人被观察到。
对于 3 号点,没有玩家在第 5 秒时在此结点,共 0 人被观察到。
对于 4 号点,玩家 1 被观察到,共 1 人被观察到。
对于 5 号点,玩家 1 被观察到,共 1 人被观察到。
对于 6 号点,玩家 3 被观察到,共 1 人被观察到。
【子任务】
每个测试点的数据规模及特点如下表所示。 提示: 数据范围的个位上的数字可以帮助判断是哪一种数据类型。
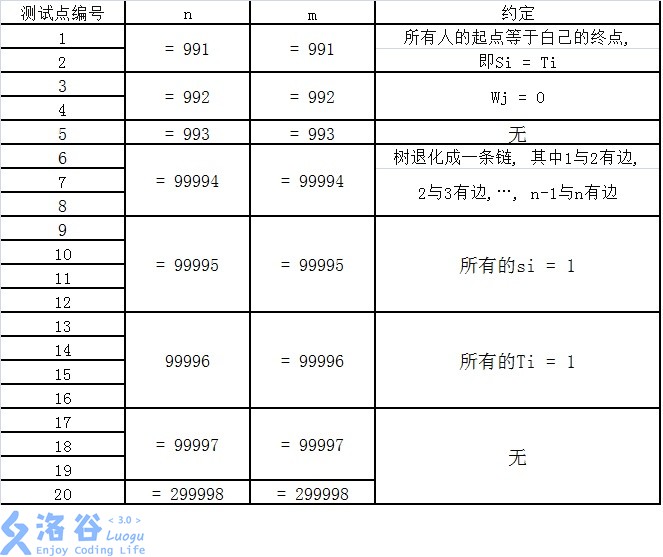
【提示】
如果你的程序需要用到较大的栈空问 (这通常意味着需要较深层数的递归), 请务必仔细阅读选手日录下的文本当rumung:/stact.p″, 以了解在最终评测时栈空问的限制与在当前工作环境下调整栈空问限制的方法。
在最终评测时,调用栈占用的空间大小不会有单独的限制,但在我们的工作环境中默认会有 8 MB 的限制。 这可能会引起函数调用层数较多时, 程序发生栈溢出崩溃。
我们可以使用一些方法修改调用栈的大小限制。 例如, 在终端中输入下列命令 ulimit -s 1048576
此命令的意义是,将调用栈的大小限制修改为 1 GB 。
例如,在选手目录建立如下 sample.cpp 或 sample.pas
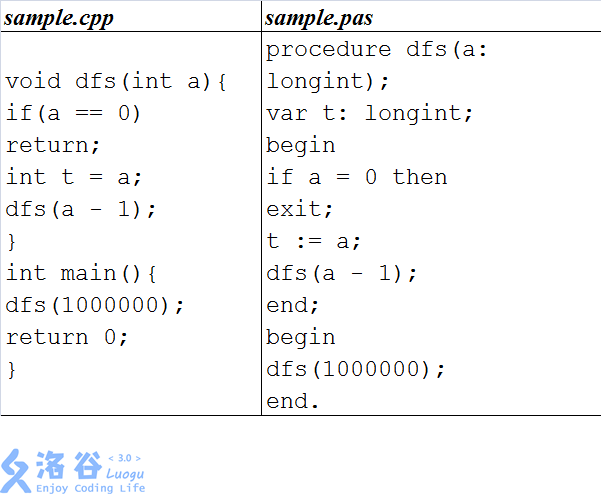
将上述源代码编译为可执行文件 sample 后,可以在终端中运行如下命令运行该程序
./sample
如果在没有使用命令“ ulimit -s 1048576”的情况下运行该程序, sample会因为栈溢出而崩溃; 如果使用了上述命令后运行该程序,该程序则不会崩溃。
特别地, 当你打开多个终端时, 它们并不会共享该命令, 你需要分别对它们运行该命令。
请注意, 调用栈占用的空间会计入总空间占用中, 和程序其他部分占用的内存共同受到内存限制。
正解:
LCA+桶+树上差分(也不能说是差分但又和差分类似)
在说正解之前,先声明一些变量:
- lcafrom [x]: 以x为LCA的起点集合。
- tofrom [x]: 以x为终点的起点集合。
- lcato [x]: 以x为LCA的终点集合。
- roadcount[x]: 以x为起点的路径条数。
另外,请记住:
正解并不是对一个个玩家进行操作,而是先对全部玩家进行一些预处理,然后用两个类似的dfs函数对整棵树处理,最后再做一些微调,就输出答案。
对于玩家在树上的路径(u,v)
我们可以对其进行拆分。
拆分成: u ---> LCA(u,v) 与 LCA(u,v) ---> v 两条路径。
对于这一步,因为我们在一开始已经说明是先对每个玩家进行预处理,
所以在这一步我们选择Tarjan版本的LCA会更好一些,因为时间复杂度会更少,
不过,用倍增求LCA对于本题来说也是不会卡的(我自己在洛谷上时间最长的一个点是0.7s左右)。
我们先考虑 u ---> LCA(u,v) 这条路径,这是一条向“上”跑的路径。
对与这条路径上的点i来说,当且仅当deep[i]+w[i] = deep[u]时,u节点对i节点是有贡献的。
那么也就是说,只要符合deep[i]+w[i]的全部是玩家起点的点,就能对i点产生贡献。
在叙述完向上的路径后,我们再来考虑向下的路径,即LCA(u,v) --->v。
对于向下走的路径,我们也思考,在什么条件下,这条路径上的点会获得贡献呢?
很明显的,当 dis(u,v)-deep[v] = w[i]-deep[i] 等式成立的时候,这条路径将会对i点有贡献。
所以,对于这道题来说,现在我们主要的思路已经完全讲完了。
但是,对于实现来说,需要注意以下几点。
- 对于桶bucket来说,我们在计算的过程中其下标可能是负值,所以我们在操作桶时要将其下标右移 MAXN 即点数。
- 如果一条路径的LCA能观察到这条路上的人,我们还需将该LCA去重。
条件是: if(deep[u] == deep[lca]+w[i])ans[lca]--;
下面贴下代码(LCA用的是倍增)

1 /* 2 Problem: P1600 天天爱跑步 3 Author: 航空信奥 4 Date: 2018/07/28 5 Description: 一个恶心的,困难的问题,咩~咩~咩~~~ 6 */ 7 8 // 注:个人习惯,数组元素下标一般从1开始 9 #pragma GCC optimize("O1") 10 #pragma GCC optimize("O2") 11 #pragma GCC optimize("O3") 12 // 不要管我,我就要皮,o1o2o3齐开,咩~~~ 13 #include <stdio.h> 14 #include <string.h> 15 #include <malloc.h> 16 #include <vector> 17 #include <map> 18 #define Char_Int(a) ((a) & 15) 19 #define Int_Char(a) ((a) + '0') 20 #define rg register 21 22 namespace hkxa { 23 template <typename _TpInt> inline _TpInt read(); 24 template <typename _TpInt> inline void write(_TpInt x); 25 template <typename _TpSwap> inline void swap(_TpSwap &x, _TpSwap &y); 26 27 # define SizeN 300007 28 # define SizeLogN 22 29 # define tong(a) bucket[a + SizeN] 30 31 int n, m; 32 int bucket[SizeN * 3]; 33 /* 使用 tong(a) 来读取桶 bucket 里面的数据,防止越界,因为在数组“桶”的使 34 用过程中,下标有可能成为负数。 */ 35 std::vector<int> lcafrom[SizeN * 2], tofrom[SizeN * 2], lcato[SizeN * 2]; 36 int roadcount[SizeN * 2]; 37 /* lcafrom [x]: 以x为LCA的起点集合 38 tofrom [x]: 以x为终点的起点集合 39 lcato [x]: 以x为LCA的终点集合 40 roadcount[x]: 以x为起点的路径条数 */ 41 int w[SizeN], ans[SizeN]; 42 /* w [x]: 观察员x观察的时间节点 43 ans[x]: 观察员x观察到的玩家人数 */ 44 int f[SizeN][SizeLogN + 1], deep[SizeN], dist[SizeN]; 45 bool use[SizeN] = {0}; 46 /* LCA用品 : f 程序算法用品 : deep, dist 47 f : 不用说了吧,大家都懂,倍增求LCA的父亲数组 48 deep : 每个节点的深度 49 dist : 距离 */ 50 51 struct EDGE { // 存储边信息 52 int e; 53 // 通往e的道路 54 EDGE *next_edge; 55 // 下一条边的指针 56 EDGE() : e(0), next_edge(NULL) {} 57 // 初始化 58 } *v[SizeN], edges[SizeN * 2]; 59 int ct_edges = 0; 60 /* v数组存储了每个点最后的连接的边(指针),edges数组是树上边的集合,ct_edges 61 是edges的top(即:上次在edges数组的ct_edges位置添加了边) */ 62 63 struct Person { 64 int s, t; 65 int lca; 66 int dis; 67 } p[SizeN]; 68 /* 存储人的信息 69 s, t: 如题意 70 lca : s, t的公共祖先LCA 71 dis : s, t之间的最短路距离 */ 72 73 inline void Add_edge(int s, int e) // 添加一条从s到e的边 74 { 75 ct_edges++; 76 edges[ct_edges].next_edge = v[s]; 77 v[s] = edges + ct_edges; // 地址赋值 78 v[s]->e = e; 79 } 80 81 inline void link(int x, int y) // 添加一条x与y之间的双向边 82 { 83 Add_edge(x, y); 84 Add_edge(y, x); 85 } 86 87 void dfs_LCA(int now, int depth) // 倍增求LCA的预处理函数 88 { 89 use[now] = true; 90 deep[now] = depth; 91 for (rg int k = 1; k <= SizeLogN; k++){ 92 int j = f[now][k - 1]; 93 f[now][k] = f[j][k - 1]; 94 } 95 for (rg EDGE *nxt = v[now]; nxt; nxt = nxt->next_edge) { 96 /* 这一行等价于 for (EDGE *nxt = v[now]; nxt != NULL; nxt = nxt->next), 97 C++里非0为真(NULL = 0) */ 98 if(!use[nxt->e]) { 99 f[nxt->e][0] = now; 100 dist[nxt->e] = dist[now] + 1; 101 dfs_LCA(nxt->e, depth + 1); 102 } 103 } 104 use[now] = false; 105 } 106 107 inline int jump(int u, int depth) { 108 for (rg int k = 0; k <= SizeLogN; k++) { 109 if ((depth & (1 << k))) u = f[u][k]; 110 } 111 return u; 112 } 113 114 inline int LCA(int u, int v){ 115 if (deep[u] < deep[v]) swap(u, v); 116 u = jump(u, deep[u] - deep[v]); 117 for (rg int k = SizeLogN; k >= 0; k--) { 118 if (f[u][k] != f[v][k]) u = f[u][k], v = f[v][k]; // 倍增,一跃而上 119 } 120 return u == v ? u : f[u][0]; 121 } 122 123 inline void dfs_fromLCA(int now) // 从from到LCA的路线 124 { 125 use[now] = true; // 打上tag 126 int prev = tong(deep[now] + w[now]); 127 for (rg EDGE *g = v[now]; g; g = g->next_edge) { 128 if (!use[g->e]) dfs_fromLCA(g->e); 129 } 130 tong(deep[now]) += roadcount[now]; 131 ans[now] += tong(deep[now] + w[now]) - prev; 132 int len = lcafrom[now].size(); 133 for (rg int k = 0; k < len; k++) { 134 tong(deep[lcafrom[now][k]])--; 135 } 136 use[now] = false; // 删除tag 137 } 138 139 inline void dfs_LCAto(int now) // 从LCA到to的路线 140 { 141 use[now] = true; // 打上tag 142 int prev = tong(w[now] - deep[now]); 143 for (rg EDGE *g = v[now]; g; g = g->next_edge) { 144 if(!use[g->e]) dfs_LCAto(g->e); 145 } 146 int len = tofrom[now].size(); 147 for (rg int k = 0; k < len; k++) { 148 tong(tofrom[now][k])++; 149 } 150 ans[now] += tong(w[now] - deep[now]) - prev; 151 len = lcato[now].size(); 152 for (rg int k = 0; k < len; k++) { 153 tong(lcato[now][k])--; 154 } 155 use[now] = false; 156 } 157 158 inline int main() 159 { 160 n = read<int>(); 161 m = read<int>(); 162 for (rg int i = 1; i <= n - 1; i++) { 163 link(read<int>(), read<int>()); 164 } 165 for (rg int i = 1; i <= n; i++) 166 w[i] = read<int>(); 167 f[1][0] = 1; 168 dfs_LCA(1, 0); // 倍增求LCA的预处理 169 int S, T; 170 for(rg int i = 1; i <= m; i++) { // 核心算法之预处理 171 S = read<int>(); 172 T = read<int>(); 173 p[i].s = S; 174 p[i].t = T; 175 p[i].lca = LCA(S, T); 176 p[i].dis = dist[S] + dist[T] - dist[p[i].lca] * 2; 177 roadcount[S]++; 178 lcafrom[p[i].lca].push_back(S); 179 tofrom[T].push_back(p[i].dis - deep[T]); 180 lcato[p[i].lca].push_back(p[i].dis - deep[T]); 181 } 182 // 核心算法 - 开始 183 dfs_fromLCA(1); // 从下至上(从from到LCA) 184 dfs_LCAto(1); // 从上至下(从LCA到to) 185 for (rg int i = 1; i <= m; i++) { 186 if(deep[p[i].s] == deep[p[i].lca] + w[p[i].lca]) { 187 ans[p[i].lca]--; 188 } 189 } 190 for (rg int i = 1; i <= n; i++) { 191 write<int>(ans[i]); 192 putchar(32); 193 } 194 return 0; 195 } 196 197 template <typename _TpInt> 198 inline _TpInt read() 199 { 200 register _TpInt flag = 1; 201 register char c = getchar(); 202 while ((c > '9' || c < '0') && c != '-') 203 c = getchar(); 204 if (c == '-') flag = -1, c = getchar(); 205 register _TpInt init = Char_Int(c); 206 while ((c = getchar()) <= '9' && c >= '0') 207 init = (init << 3) + (init << 1) + Char_Int(c); 208 return init * flag; 209 } 210 211 template <typename _TpInt> 212 inline void write(_TpInt x) 213 { 214 if (x < 0) { 215 putchar('-'); 216 write<_TpInt>(~x + 1); 217 } 218 else { 219 if (x > 9) write<_TpInt>(x / 10); 220 putchar(Int_Char(x % 10)); 221 } 222 } 223 224 template <typename _TpSwap> 225 inline void swap(_TpSwap &x, _TpSwap &y) 226 { 227 _TpSwap t = x; 228 x = y; 229 y = t; 230 } 231 } 232 233 int main() 234 { 235 // system("ulimit -s 1048576"); 236 hkxa::main(); 237 return 0; 238 }
完美结束。
我是不会告诉你我调了6个小时的!!!



