算法入门

算法介绍

算法（Algorithm）：⼀个计算过程，解决问题的⽅法

Niklaus Wirth: “程序=数据结构+算法”

时间复杂度

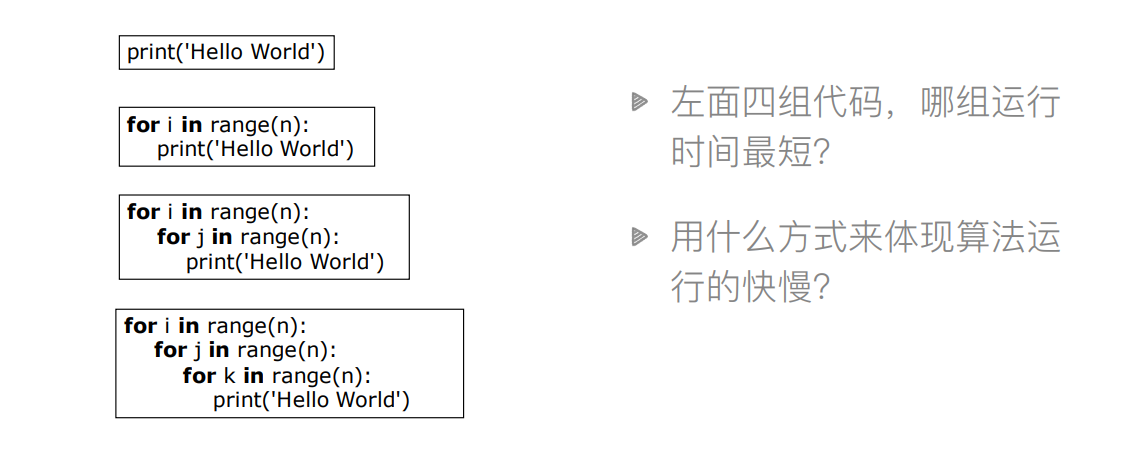
简单总结

时间复杂度是⽤来估计算法运⾏时间的⼀个式⼦（单位）。

⼀般来说，时间复杂度⾼的算法⽐复杂度低的算法慢。

常⻅的时间复杂度（按效率排序）：O(1)<O(log n)<O(n)<O(n log n)<O(n²)<O(n² log n)<O(n³)...

复杂问题的时间复杂度：O(n!) o(2ⁿ)O(nⁿ) ...

如何简单快速地判断算法复杂度

快速判断算法复杂度（适⽤于绝⼤多数简单情况）：

确定问题规模n
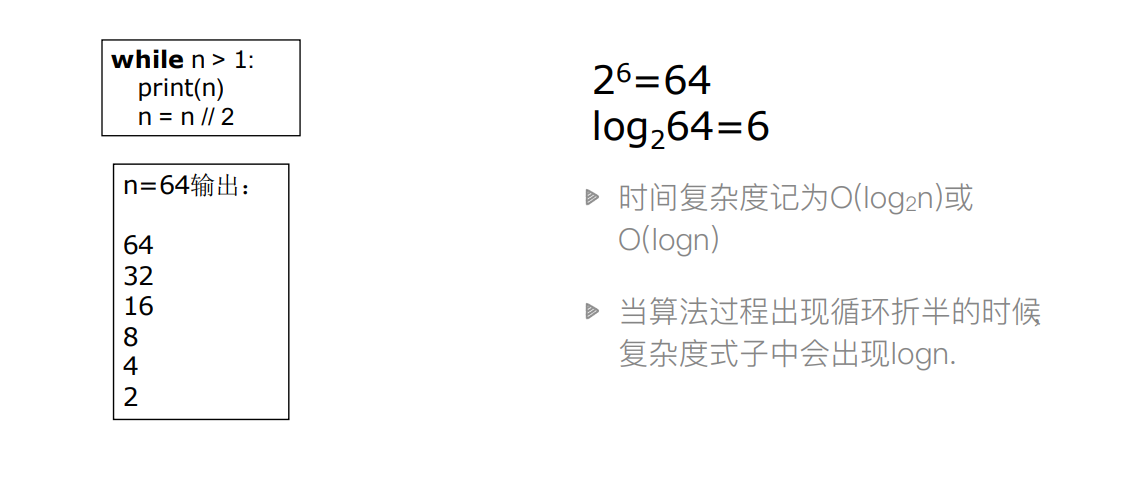
循环减半过程→log n
k层关于n的循环→n^k

复杂情况：根据算法执⾏过程判断

空间复杂度

空间复杂度：⽤来评估算法内存占⽤⼤⼩的式⼦

空间复杂度的表示⽅式与时间复杂度完全⼀样

算法使⽤了⼏个变量：O(1)
算法使⽤了⻓度为n的⼀维列表：O(n）
算法使⽤了m⾏n列的⼆维列表：O(mn)

“用空间换时间”

递归

下面哪个是递归？

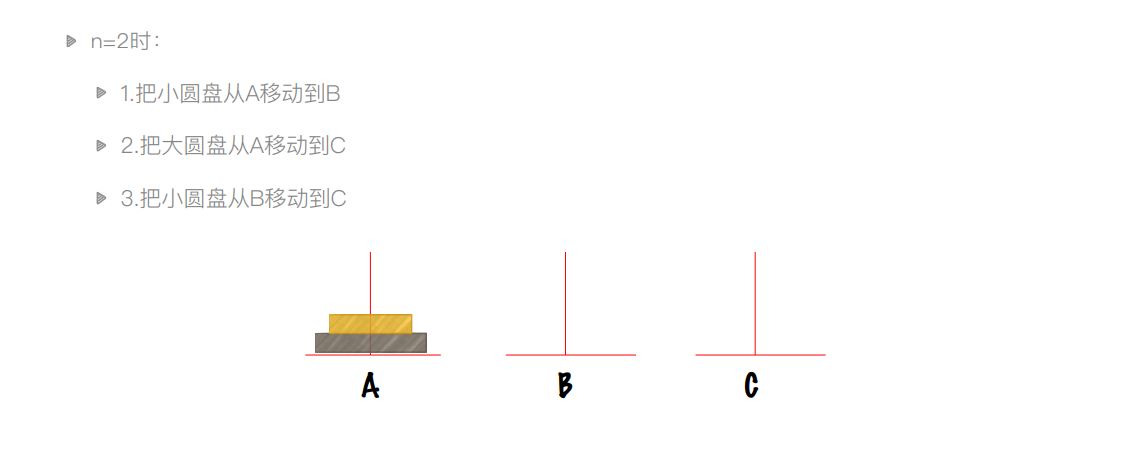
递归实例：汉诺塔问题

python程序实现

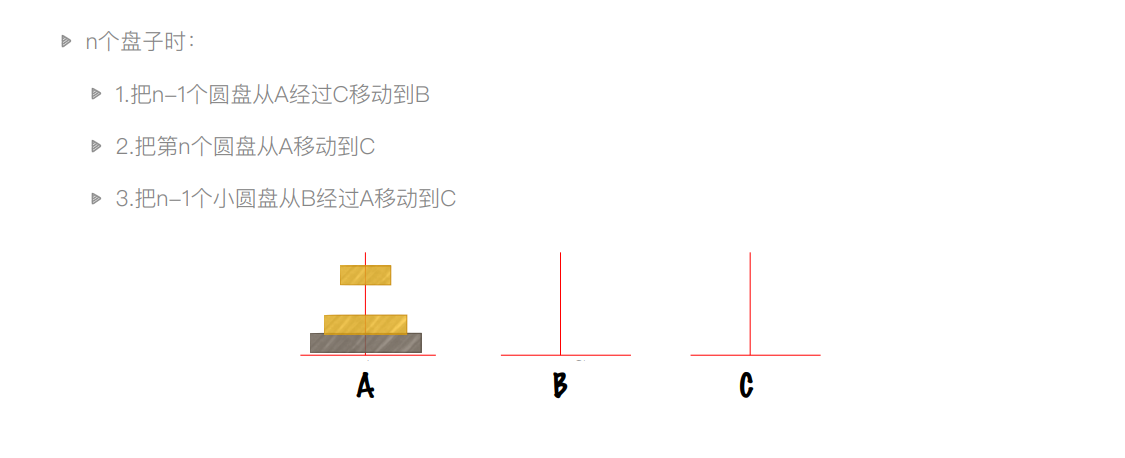
# 目的是将n个圆盘从a经过b移动到c
def hanoi(n, a, b, c):
    if n > 0:
        # 第一步：将n-1个圆盘从a经过c移动到b
        hanoi(n - 1, a, c, b)
        # 第二步：将第n个圆盘从a移动到c
        print("%d: moving from %s to %s." % (n, a, c))
        # 第三步：将n-1个圆盘从b经过a移动到c
        hanoi(n - 1, b, a, c)
hanoi(3, "a", "b", "c")

汉诺塔移动次数的递推式：h(x)=2h(x-1)+1
h(64)=18446744073709551615
假设婆罗⻔每秒钟搬⼀个盘⼦，则总共需要5800亿年！

列表查找

什么是列表查找
顺序查找
⼆分查找

查找

查找：在⼀些数据元素中，通过⼀定的⽅法找出与给定关键字相同的数据元素的过程。

列表查找（线性表查找）：从列表中查找指定元素

输⼊：列表、待查找元素
输出：元素下标（未找到元素时⼀般返回None或-1）

内置列表查找函数：index()

顺序查找 (Linear Search)

顺序查找：也叫线性查找，从列表第⼀个元素开始，顺序进⾏搜索，直到找到元素或搜索到列表最后⼀个元素为⽌。

时间复杂度：O(n)

python程序实现

"""顺序查找"""
def linear_search(lst, val):
    for index, value in enumerate(lst):
        if value == val:
            return index
    return
ret = linear_search([9, 8, 6, 2, 1, 4], 2)
print(ret)

二分查找 (Binary Search)

⼆分查找：⼜叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的⽐较，可以使候选区减少⼀半。

时间复杂度：O(log n)

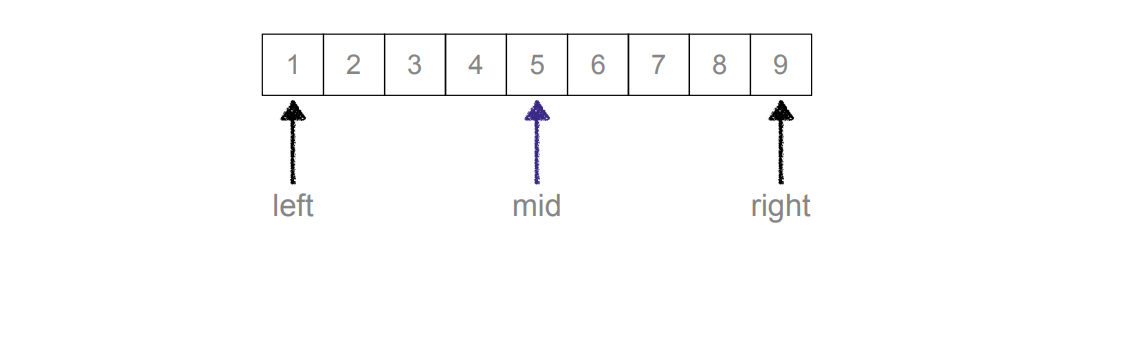
python程序实现

"""二分查找(必须是排好序的内容)"""
def binary_search(lst, val):
    low = 0
    high = len(lst) - 1
    while low <= high:
        mid = (low + high) // 2
        if val > lst[mid]:
            low = mid + 1
        elif val < lst[mid]:
            high = mid - 1
        else:
            return mid
    return
ret = binary_search([1, 2, 3, 4, 5, 6, 7, 8, 9], 3)
print(ret)

列表排序

排序：将⼀组“⽆序”的记录序列调整为“有序”的记录序列。

列表排序：将⽆序列表变为有序列表

输⼊：列表
输出：有序列表

升序与降序

内置排序函数：sort()

常⻅排序算法

排序Low B三⼈组	排序NB三⼈组	其他排序
冒泡排序	快速排序	希尔排序
选择排序	堆排序	计数排序
插⼊排序	归并排序	基数排序

冒泡排序 (Bubble Sort)

列表每两个相邻的数，如果前⾯⽐后⾯⼤，则交换这两个数。⼀趟排序完成后，则⽆序区减少⼀个数，有序区增加⼀个数。

代码关键点：趟、⽆序区范围

时间复杂度：O(n²)

python程序实现

"""冒泡排序"""
import random
# def bubble_sort(lst):
#     for i in range(len(lst) - 1):
#         for j in range(i + 1, len(lst)):
#             if lst[i] >= lst[j]:
#                 lst[i], lst[j] = lst[j], lst[i]
#         # print(lst)
#     return lst
def bubble_sort(lst):
    for i in range(len(lst) - 1):
        for j in range(len(lst) - i - 1):
            if lst[j] > lst[j + 1]:
                lst[j], lst[j + 1] = lst[j + 1], lst[j]
        # print(lst)
    return lst
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
ret = bubble_sort(lst)
print(ret)

冒泡排序-优化

如果冒泡排序中的⼀趟排序没有发⽣交换，则说明列表已经有序，可以直接结束算法。

python程序实现

import random
def bubble_sort_advanced(lst):
    # 冒泡排序优化
    for i in range(len(lst) - 1):
        flag = False
        for j in range(len(lst) - i - 1):
            if lst[j] > lst[j + 1]:
                lst[j], lst[j + 1] = lst[j + 1], lst[j]
                flag = True
        if not flag:
            break
        print(lst)
    return lst
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
ret = bubble_sort_advanced(lst)
print(ret)

选择排序 (Select Sort)

⼀趟排序记录最⼩的数，放到第⼀个位置，再⼀趟排序记录记录列表⽆序区最⼩的数，放到第⼆个位置……

算法关键点：有序区和⽆序区、⽆序区最⼩数的位置

时间复杂度：O(n²)

python程序实现

"""选择排序"""
import random
def select_sort_simple(lst):
    # 简单版
    # 每一趟找出最小的数，放到列表中
    ret_list = []
    for i in range(len(lst)):
        min_num = min(lst)
        ret_list.append(min_num)
        lst.remove(min_num)
    return ret_list
def select_sort(lst):
    for i in range(len(lst) - 1):
        mix_loc = i  # 记录最小的坐标
        for j in range(i + 1, len(lst)):
            if lst[j] < lst[mix_loc]:
                mix_loc = j
        lst[i], lst[mix_loc] = lst[mix_loc], lst[i]
    return lst
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
# ret = select_sort_simple(lst)
ret = select_sort(lst)
print(ret)

直接插入排序

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

时间复杂度：O(n²)

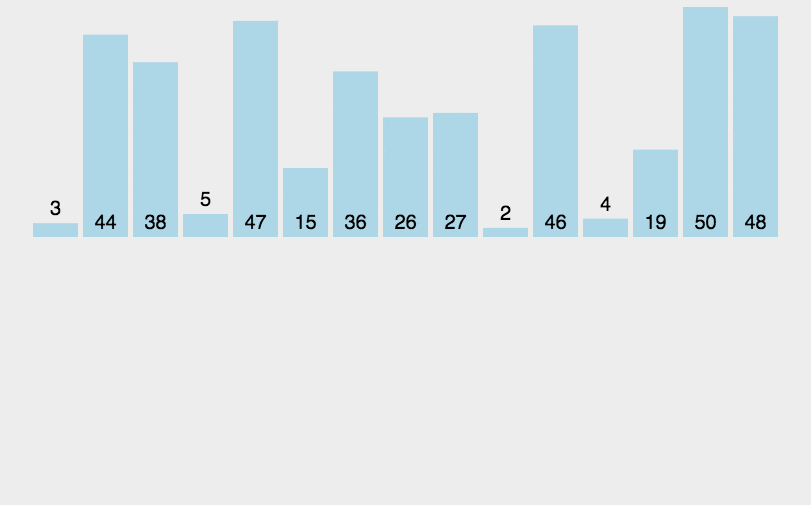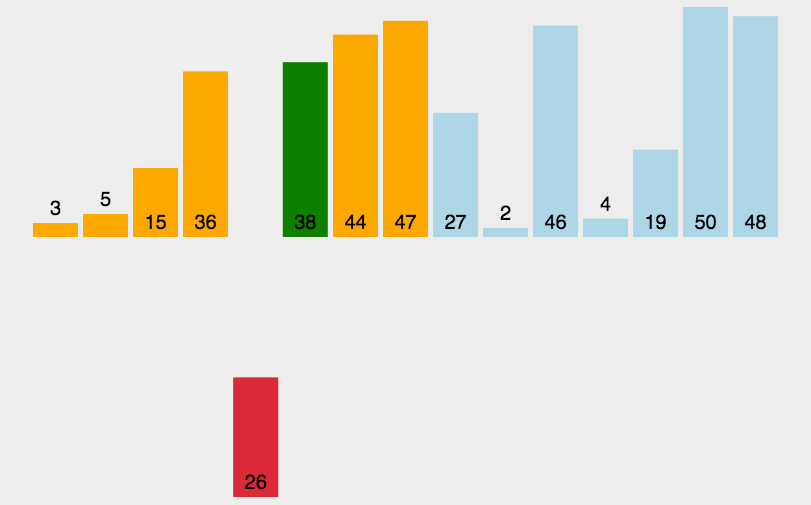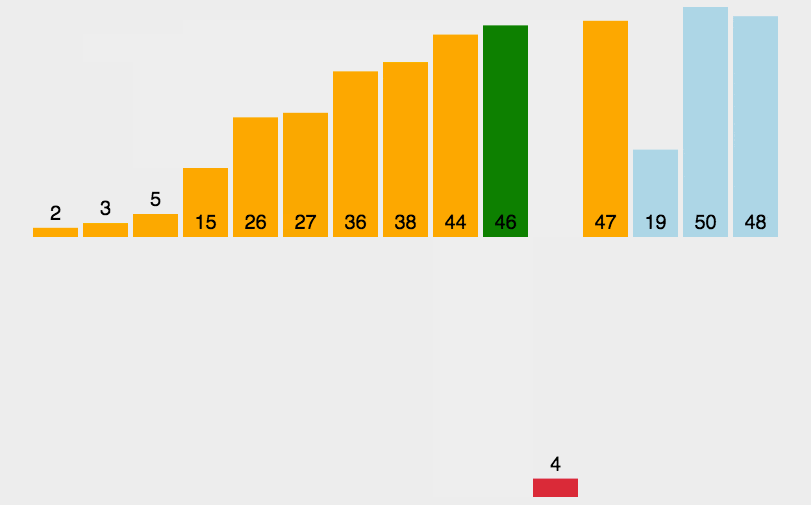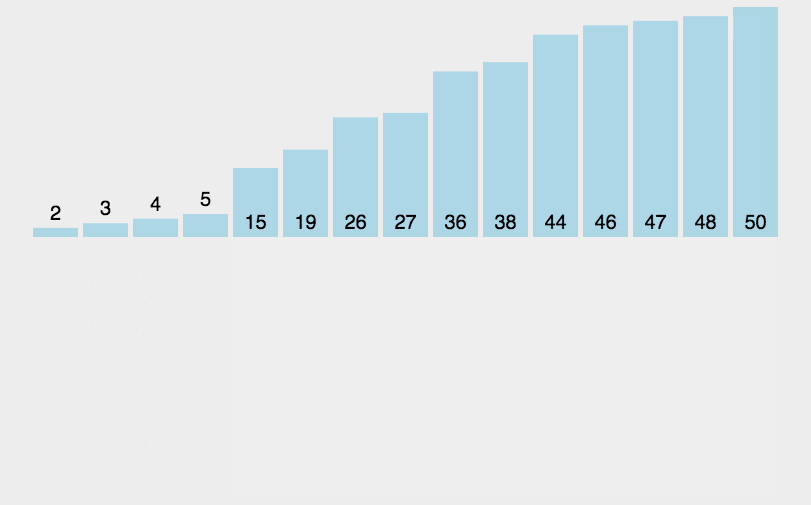
python程序实现

"""直接插入排序"""
import random
def insert_sort(lst):
    for i in range(1, len(lst)):  # 第一个是有序区
        current_val = lst[i]
        j = i - 1
        while current_val < lst[j] and j >= 0:
            lst[j + 1] = lst[j]
            j -= 1
        lst[j + 1] = current_val
    return lst
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
ret = insert_sort(lst)
print(ret)

折半插入排序

在直接插入排序的基础上更进一层，在插入前面有序序列时使用二分查找插入。

时间复杂度仍然为O(n²)，但它的效果还是比直接插入排序要好。

最好时间复杂度O(n)，平均时间复杂度O(n²)，最坏时间复杂度O(n²)。

空间复杂度为O(1)。

快速排序

快速排序的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要小，再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列。

快速排序实现：

取⼀个元素p（第⼀个元素），使元素p归位；
列表被p分成两部分，左边都⽐p⼩，右边都⽐p⼤；
递归完成排序。

时间复杂度：O(n log n)

python程序实现

"""快速排序"""
import random
# 方式一
# def quick_sort(arr, left=None, right=None):
#     left = 0 if not isinstance(left, (int, float)) else left
#     right = len(arr) - 1 if not isinstance(right, (int, float)) else right
#     if left < right:
#         partitionIndex = partition(arr, left, right)
#         quick_sort(arr, left, partitionIndex - 1)
#         quick_sort(arr, partitionIndex + 1, right)
#     return arr
# def partition(arr, left, right):
#     pivot = left
#     index = pivot + 1
#     i = index
#     while i <= right:
#         if arr[i] < arr[pivot]:
#             swap(arr, i, index)
#             index += 1
#         i += 1
#     swap(arr, pivot, index - 1)
#     return index - 1
# def swap(arr, i, j):
#     arr[i], arr[j] = arr[j], arr[i]
# 方式二
def quick_sort(lst):
    # 让外界之传入一个参数即可
    _quick_sort(lst, 0, len(lst) - 1)
def _quick_sort(lst, left, right):
    if left < right:
        mid = partition(lst, left, right)
        _quick_sort(lst, left, mid - 1)
        _quick_sort(lst, mid + 1, right)
def partition(lst, left, right):
    current = lst[left]  # 选取第一个值为分割点
    while left < right:  # left和right相等时结束
        while current <= lst[right] and left < right:
            right -= 1
        lst[left] = lst[right]
        while current >= lst[left] and left < right:
            left += 1
        lst[right] = lst[left]
    lst[left] = current  # 最后把选取的值放到左边的空位中
    return left  # 最后left和right是相等的，返回哪个都一样
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
quick_sort(lst, 0, len(lst) - 1)
print(lst)

堆排序

堆排序前传-树与二伹树

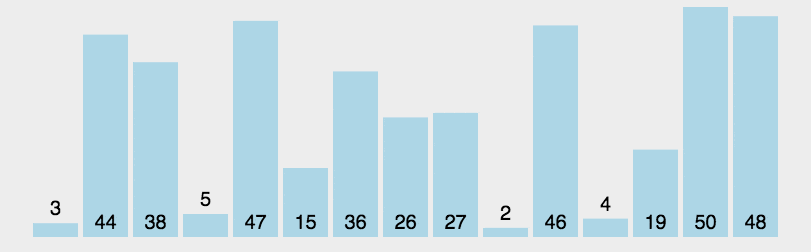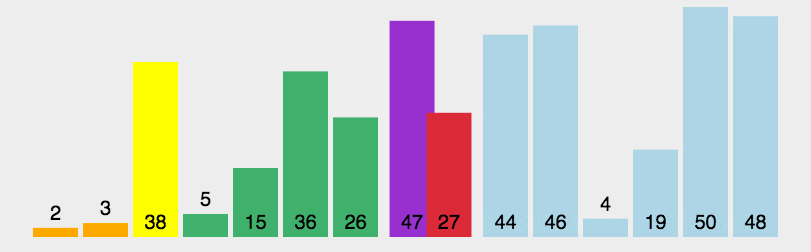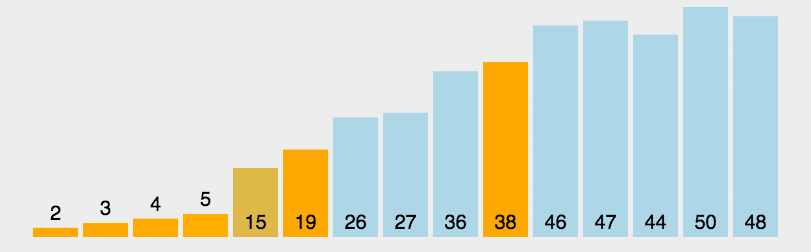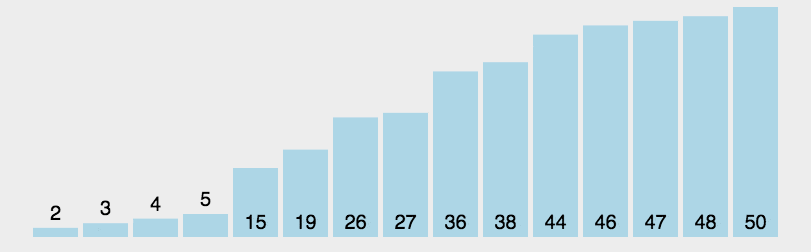
⼀些概念：（以上图举例）

根节点、叶⼦节点：A为根节点，B、C、H、I、K、L、M、N、P、Q为叶子节点（下面没有节点叫叶子节点）

树的深度（⾼度）：4（多少层）

树的度：树内各结点最大的度（A节点为最大度-6）

孩⼦节点/⽗节点：上面的叫父节点，下面开发的分支叫孩子节点

⼦树：开发出来的分支可以组成一棵树称为子树

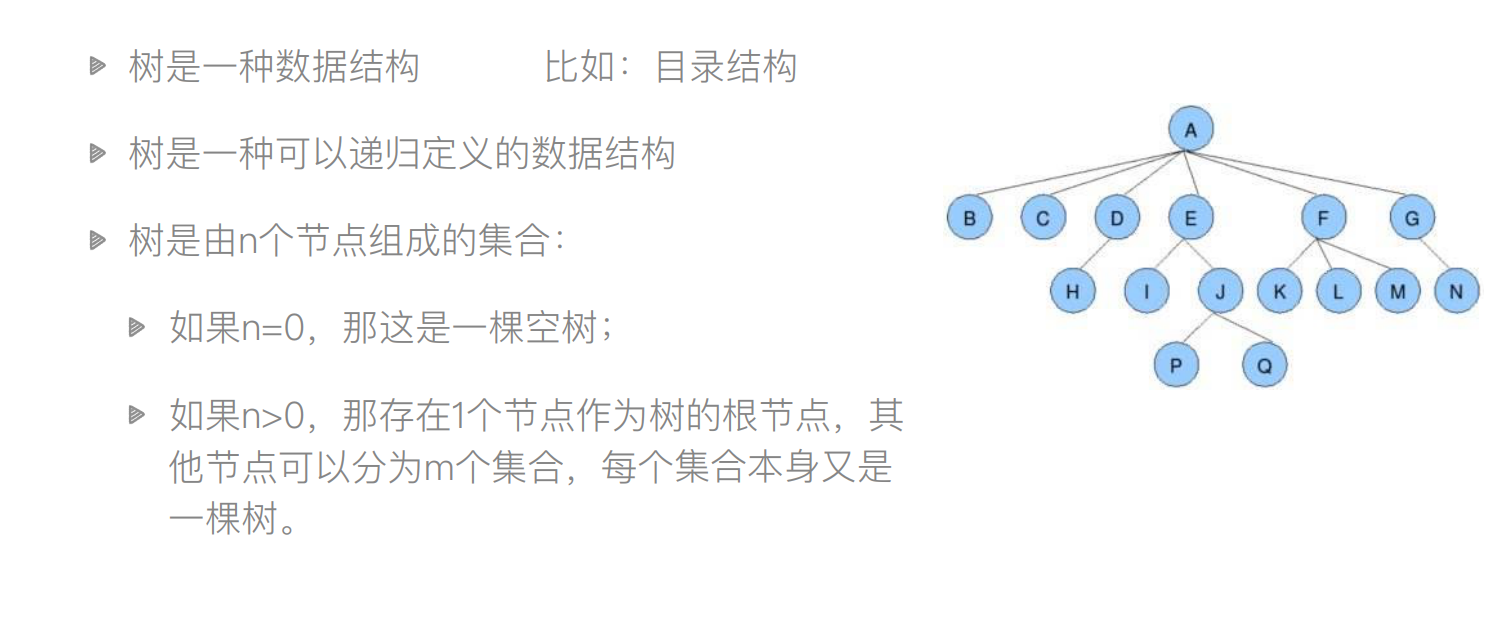
堆排序前传-二叉树

⼆叉树：度不超过2的树

每个节点最多有两个孩⼦节点

两个孩⼦节点被区分为左孩⼦节点和右孩⼦节点

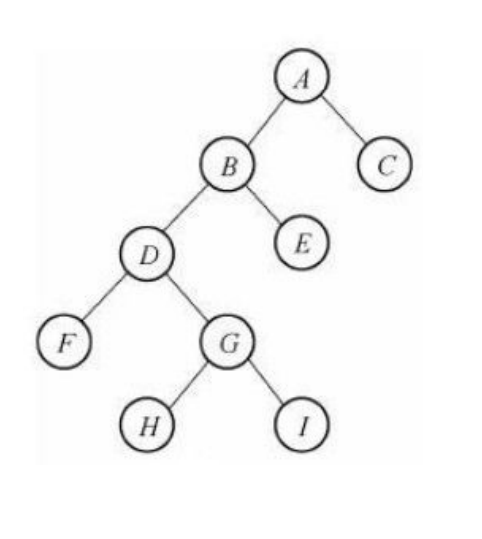
堆排序前传-完全二伹树

满⼆叉树：⼀个⼆叉树，如果每⼀个层的结点数都达到最⼤值，则这个⼆叉树就是满⼆叉树。

完全⼆叉树：叶节点只能出现在最下层和次下层，并且最下⾯⼀层的结点都集中在该层最左边的若⼲位置的⼆叉树。（在满二叉树的基础上可以从后面剔除掉几个节点）

堆排序前传-二叉树的存储方式

分为链式存储⽅式和顺序存储⽅式

二叉树的顺序存储方式

下标推出

父节点推出左孩子结点：2i+1

父节点推出右孩子结点：2i+2

左孩子推出父节点：i//2

右孩子推出父节点：i//2-1

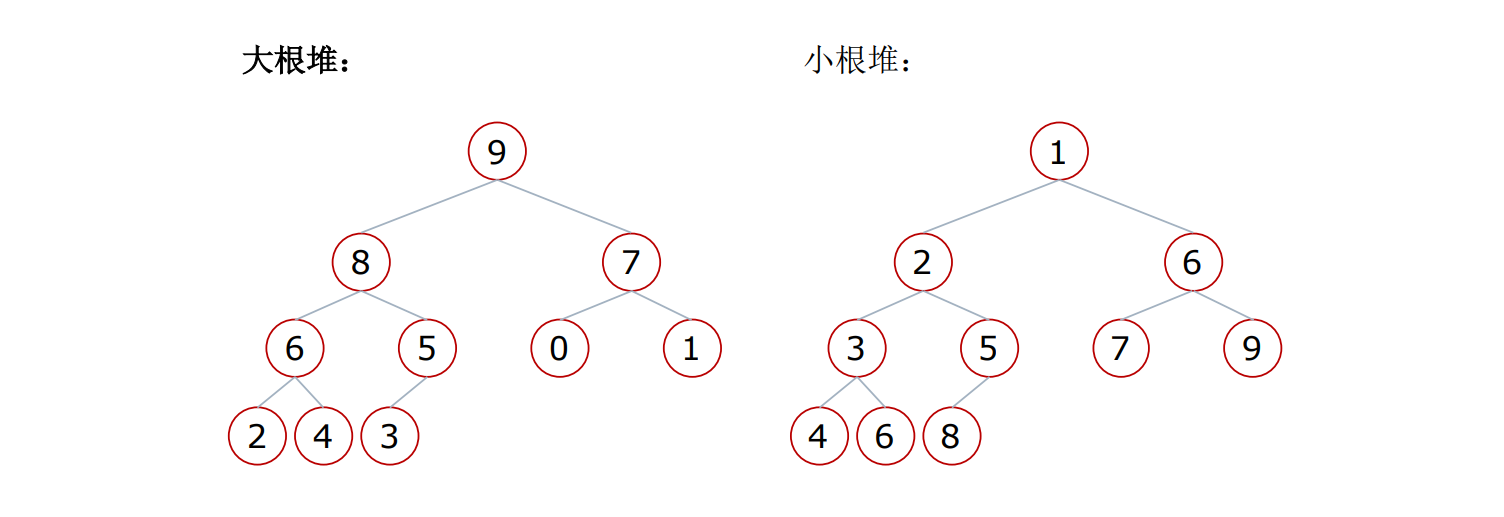
堆排序-什么是堆

堆：⼀种特殊的完全⼆叉树结构

⼤根堆：⼀棵完全⼆叉树，满⾜任⼀节点都⽐其孩⼦节点⼤

⼩根堆：⼀棵完全⼆叉树，满⾜任⼀节点都⽐其孩⼦节点⼩

堆排序-堆的向下调整性质

假设根节点的左右⼦树都是堆，但根节点不满⾜堆的性质，可以通过⼀次向下的调整来将其变成⼀个堆。

堆排序过程

1.建⽴堆。

2.得到堆顶元素，为最⼤元素。

3.去掉堆顶，将堆最后⼀个元素放到堆顶，此时可通过⼀次调整重新使堆有序。

4.堆顶元素为第⼆⼤元素。

5.重复步骤3，直到堆变空。

python代码实现

"""堆排序"""
import random
def sift(lst, low, high):
    """
    堆的向下编排函数（大根堆），每一次编排让堆变得有序
    :param lst: 列表
    :param low: 堆顶（堆的根位置）
    :param high: 堆尾（堆的最后一个位置）
    :return:
    """
    i = low  # i首先表示第一行
    j = 2 * i + 1  # j表示i的左节点
    tmp = lst[low]  # 拿到此时的堆顶
    while j <= high:  # 确保左节点有值
        if j + 1 <= high and lst[j] < lst[j + 1]:  # 判断左右孩子节点哪个大，并且j+1也就是右节点没有越出堆的底部
            j += 1  # 如果右节点大，则j指向右节点
        if tmp < lst[j]:  # 如果拿到的值比堆下面的值小，就让下面的比较大的值上来
            lst[i] = lst[j]  # 下面的值上去
            i = j  # i和j往下一层
            j = 2 * i + 1
        else:
            lst[i] = tmp  # 如果拿到的值比下面的值大，表示不用替换，堆已经形成，并且结束循环
            break
    else:
        lst[i] = tmp  # 没有左节点
def heap_sort(lst):
    n = len(lst)
    # 建堆
    for i in range(n // 2 - 1, -1, -1):  # i表示每次建堆的根节点的下标
        sift(lst, i, n - 1)
    # 出数
    for i in range(n - 1, -1, -1):  # i指向当前堆的最后一个元素
        lst[0], lst[i] = lst[i], lst[0]  # 将最大的元素依次放到堆尾
        sift(lst, 0, i - 1)  # 进行一次堆编排调整使得堆有序，i-1是新的high，此前的high的位置存放当前最大值
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
heap_sort(lst)
print(lst)

堆排序-内置模块

Python内置模块——heapq

常⽤函数：heapify(x)，heappush(heap,item)，heappop(heap)

堆排序-topk问题

问题：现在有n个数，设计算法得到前k⼤的数。（k<n）

解决思路：

取列表前k个元素建⽴⼀个⼩根堆。堆顶就是⽬前第k⼤的数。

依次向后遍历原列表，对于列表中的元素，如果⼩于堆顶，则忽略该元素；如果⼤于堆顶，则将堆顶更换为该元素，并且对堆进⾏⼀次调整；

遍历列表所有元素后，倒序弹出堆顶。

python代码实现

"""堆排序---topk问题"""
import random
def sift(lst, low, high):
    """
    堆的向下编排函数（小根堆），每一次编排让堆变得有序
    :param lst: 列表
    :param low: 堆顶（堆的根位置）
    :param high: 堆尾（堆的最后一个位置）
    :return:
    """
    i = low  # i首先表示第一行
    j = 2 * i + 1  # j表示i的左节点
    tmp = lst[low]  # 拿到此时的堆顶
    while j <= high:  # 确保左节点有值
        if j + 1 <= high and lst[j] > lst[j + 1]:  # 判断左右孩子节点哪个大，并且j+1也就是右节点没有越出堆的底部
            j += 1  # 如果右节点大，则j指向右节点
        if tmp > lst[j]:  # 如果拿到的值比堆下面的值小，就让下面的比较大的值上来
            lst[i] = lst[j]  # 下面的值上去
            i = j  # i和j往下一层
            j = 2 * i + 1
        else:
            lst[i] = tmp  # 如果拿到的值比下面的值大，表示不用替换，堆已经形成，并且结束循环
            break
    else:
        lst[i] = tmp  # 没有左节点
def topk(lst, k):
    """
    :param lst: 列表
    :param num: 要取出的最大的前几数值
    :return:
    """
    head = lst[:k]
    # 建堆
    for i in range(k // 2 - 1, -1, -1):
        sift(head, i, k - 1)
    # 遍历
    for i in range(k - 1, len(lst) - 1):
        if lst[i] > lst[0]:
            lst[0] - lst[i]
            sift(head, 0, k - 1)
    # 出数
    for i in range(k - 1, -1, -1):
        head[0], head[i] = head[i], head[0]
        sift(head, 0, i - 1)
    return head
lst = [random.randrange(10, 99) for i in range(100)]
print(lst)
head_lst = topk(lst, 10)
print(head_lst)

归并排序

python的排序是在归并排序的基础上演变而来的。

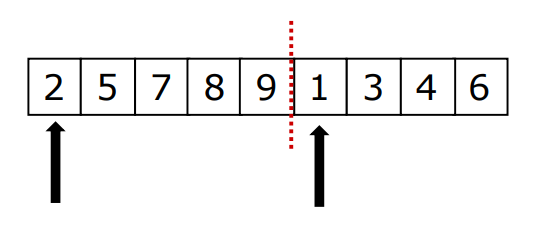
假设现在的列表分两段有序，如何将其合成为⼀个有序列表

完成一次这种操作称为⼀次归并。

分为左右两段，在直接插入排序的基础上递归的去解决。

归并排序

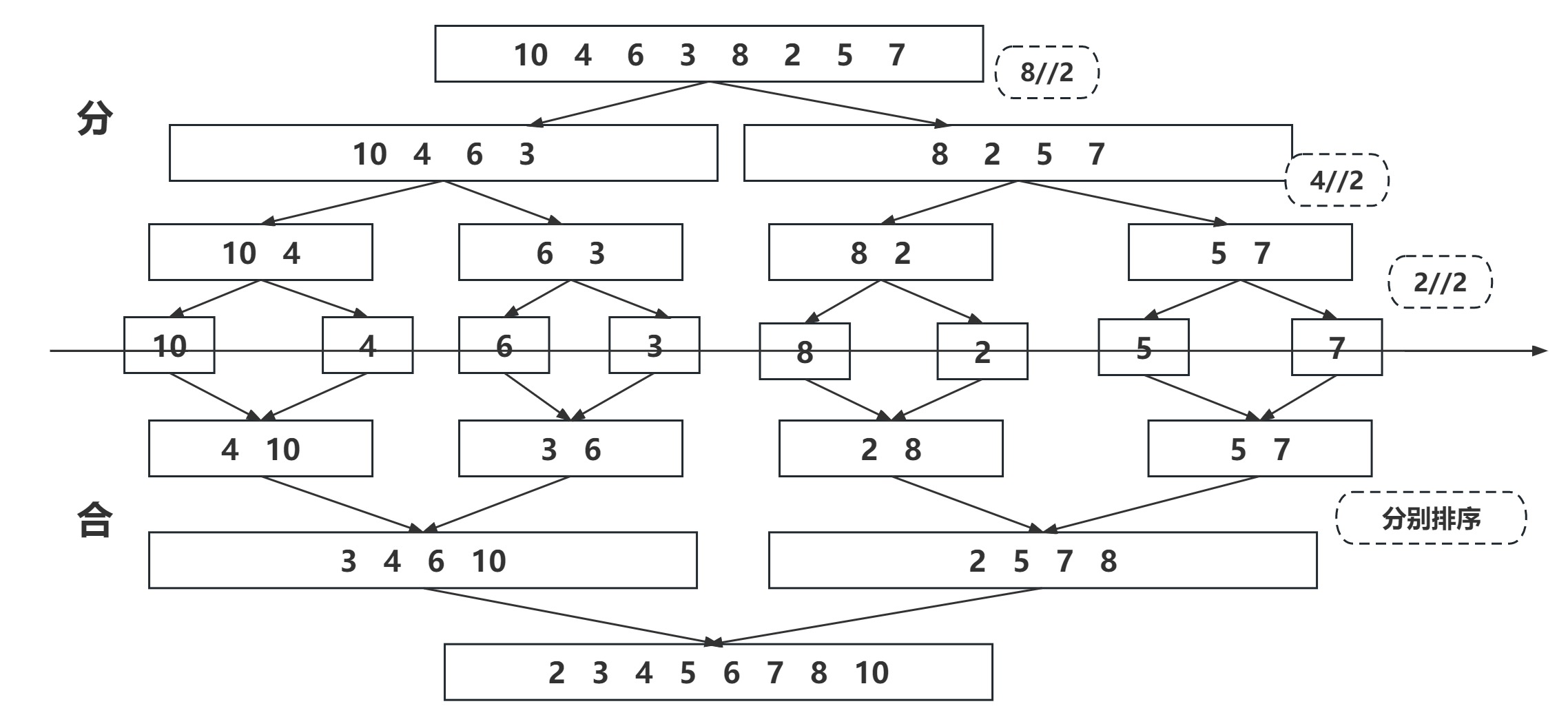
思路：

分解：将列表越分越⼩，直⾄分成⼀个元素。
终⽌条件：⼀个元素是有序的。
合并：将两个有序列表归并，列表越来越⼤。

时间复杂度：O(nlogn)

python代码实现

"""归并排序"""
import random
def merge(lst, low, mid, high):
    """
    完成一次归并
    :param lst: 列表
    :param low: 左端的起点
    :param mid: 左端的终点
    :param high: 右端(整体)的终点
    :return:
    """
    i = low  # 列表左端开头
    j = mid + 1  # 列表右端开头
    tmp_list = []
    while i <= mid and j <= high:
        if lst[i] < lst[j]:
            tmp_list.append(lst[i])
            i += 1
        else:
            tmp_list.append(lst[j])
            j += 1
    # 跳出循环说明 左端或右端的列表循环完了
    while i <= mid:  # 如果是左边没有循环完
        tmp_list.append(lst[i])
        i += 1
    while j <= high:  # 如果是右边没有循环完
        tmp_list.append(lst[j])
        j += 1
    # 赋值给原来的列表
    lst[low:high + 1] = tmp_list
def _merge_sort(lst, low, high):
    if low < high:  # low等于high说明列表只有一个元素
        mid = (low + high) // 2
        _merge_sort(lst, low, mid)  # 左边排序
        _merge_sort(lst, mid + 1, high)  # 右边排序
        merge(lst, low, mid, high)  # 归并一次
def merge_sort(lst):
    # 让外界只传入一个列表即可
    _merge_sort(lst, 0, len(lst) - 1)
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
merge_sort(lst)
print(lst)

NB三人组小结

三种排序算法的时间复杂度都是O(nlogn)

⼀般情况下，就运⾏时间⽽⾔：快速排序 < 归并排序 < 堆排序

三种排序算法的缺点：

快速排序：极端情况下排序效率低
归并排序：需要额外的内存开销
堆排序：在快的排序算法中相对较慢

排序⽅法	时间复杂度最坏情况平均情况最好情况	空间复杂度	稳定性	代码复杂度
冒泡排序	`O(n2) O(n2) O(n)`	O(1)	稳定	简单
直接选择排序	`O(n2) O(n2) O(n2)`	O(1)	不稳定	简单
直接插⼊排序	`O(n2) O(n2) O(n2)`	O(1)	稳定	简单
快速排序	`O(n2) O(nlogn) O(nlogn)`	平均情况O(logn)；最坏情况O(n)	不稳定	较复杂
堆排序	`O(nlogn) O(nlogn) O(nlogn)`	O(1)	不稳定	复杂
归并排序	`O(nlogn) O(nlogn) O(nlogn)`	O(n)	稳定	较复杂

希尔排序

希尔排序(Shell Sort)是⼀种分组插⼊排序算法。

⾸先取⼀个整数d1=n/2，将元素分为d1个组，每组相邻量元素之间距离为d1，在各组内进⾏直接插⼊排序；

取第⼆个整数d2=d1/2，重复上述分组排序过程，直到 di=1，即所有元素在同⼀组内进⾏直接插⼊排序。

希尔排序每趟并不使某些元素有序，⽽是使整体数据越来越接近有序；最后⼀趟排序使得所有数据有序。

时间复杂度讨论：https://en.wikipedia.org/wiki/Shellsort#Gap_sequences

希尔排序的时间复杂度讨论⽐较复杂，并且和选取的gap序列有关。

python代码实现

"""希尔排序"""
import random
def insert_shell_gap(lst, gap):
    # 在直接插入排序的基础上将原来的1都改为gap
    for i in range(gap, len(lst)):
        tmp = lst[i]
        j = i - gap
        while j >= 0 and tmp < lst[j]:
            lst[j + gap] = lst[j]
            j -= gap
        lst[j + gap] = tmp
def shell_sort(lst):
    gap = len(lst) // 2
    while gap >= 1:
        insert_shell_gap(lst, gap)
        gap //= 2
lst = [random.randrange(10, 99) for i in range(10)]
print(lst)
shell_sort(lst)
print(lst)

计数排序

对列表进⾏排序，已知列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。

计数排序（Counting Sort）是一种针对于特定范围之间的整数进行排序的算法。它通过统计给定数组中不同元素的数量（类似于哈希映射），然后对映射后的数组进行排序输出即可。

缺点：要知道列表中最大的值，才能开辟多少的空间。并且当值分散不均匀时，可能浪费空间。（第一个桶占%1的数值，最后一个桶占%99的数值...）

python代码实现

"""计数排序"""
import random
def count_sort(lst, max_count=100):
    """
    :param lst: 列表
    :param max_count: 列表中最大的数值
    :return:
    """
    tmp_list = [0 for i in range(max_count + 1)]  # 长度为max_count的全为0的数组
    for val in lst:
        tmp_list[val] += 1
    i = 0
    for index, value in enumerate(tmp_list):
        for v in range(value):
            lst[i] = index
            i += 1
lst = [random.randrange(1, 99) for i in range(100)]
print(lst)
count_sort(lst)
print(lst)

桶排序

在计数排序中，如果元素的范围⽐较⼤（⽐如在1到1亿之间），如何改造算法？

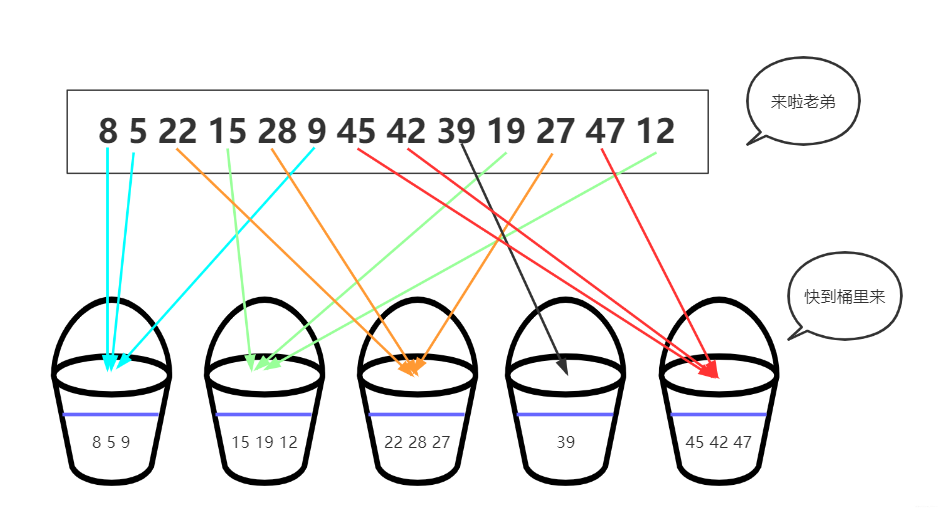
桶排序(Bucket Sort)：⾸先将元素分在不同的桶中，在对每个桶中的元素排序。桶排序是一种用空间换取时间的排序。

元素分布在桶中：

然后，元素在每个桶中排序：

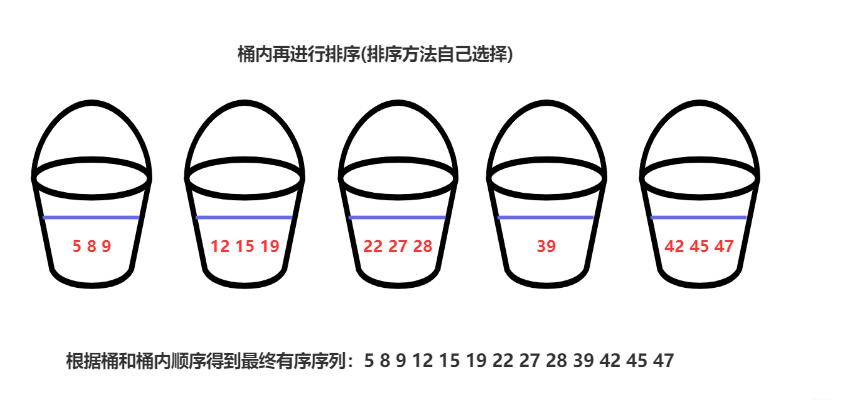
桶排序-复杂度

桶排序的表现取决于数据的分布。也就是需要对不同数据排序时采取不同的分桶策略。

平均情况时间复杂度：O(n+k)

最坏情况时间复杂度：O(n2k)

空间复杂度：O(nk)

python代码实现

"""桶排序"""
import random
def bucket_sort(lst, num=10, max_num=1000):
    """
    :param lst: 列表
    :param num: 桶的数量
    :param max_num: 最大数值
    :return:
    """
    tmp_list = [[] for _ in range(num)]  # 创建桶（二维数组）
    for value in lst:
        n = min(value // (max_num // num), num - 1)  # n表示将数值填入第几号桶（最大的数值要填入最后一个桶，所以要min一下）
        tmp_list[n].append(value)
        # 桶内排序
        for i in range(len(tmp_list[n]) - 1, -1, -1):
            if i - 1 >= 0 and tmp_list[n][i] < tmp_list[n][i - 1]:  # 如果前面的比后面的大，就换下位置
                tmp_list[n][i], tmp_list[n][i - 1] = tmp_list[n][i - 1], tmp_list[n][i]
            else:
                break
    # 将所有桶内元素放到新列表中
    sorted_list = []
    for li in tmp_list:
        sorted_list.extend(li)
    return sorted_list
lst = [random.randrange(1, 999) for i in range(10)]
print(lst)
sorted_list = bucket_sort(lst)
print(sorted_list)

基数排序

基数排序（Radix sort）是一种非比较型整数排序算法。

原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。基数排序的方式可以采用LSD（Least significant digital）或MSD（Most significant digital），LSD的排序方式由键值的最右边开始，而MSD则相反，由键值的最左边开始。

MSD：先从高位开始进行排序，在每个关键字上，可采用计数排序
LSD：先从低位开始进行排序，在每个关键字上，可采用桶排序

例如----多关键字排序：假如现在有⼀个员⼯表，要求按照薪资排序，薪资相同的员⼯再按照年龄排序。

时间复杂度：O(kN)，空间复杂度：O(k+N)，k表示数字的位数。

python代码实现

"""
基数排序
两种方法的不同在于如何看待最大数的位数
"""
import random
import math
# 方法一
def radix_sort(lst, num=10):
    """
    :param lst: 列表
    :param num: 桶的数量
    :return:
    """
    max_value = max(lst)  # 拿到最大的数
    length = int(math.log(max_value, 10)) + 1  # 直接获取最大数的位数，log的第二个参数表示以什么为底
    i = 0
    while length > 0:
        bucket_list = [[] for _ in range(num)]  # 创建桶
        for value in lst:
            # ps: 987 i=0:987%10-->7 i=1:987//10%10-->8 i=2:987//100%10-->9
            digit = value // 10 ** i % 10  # 求出当前数的个位、百位、千位...
            bucket_list[digit].append(value)
        lst.clear()
        for li in bucket_list:
            lst.extend(li)
        length -= 1
        i += 1
# 方法二
def radix_sort(lst, num=10):
    """
    :param lst: 列表
    :param num: 桶的数量
    :return:
    """
    max_value = max(lst)  # 拿到最大的数
    i = 0  # 不直接获取最大数的位数
    while 10 ** i <= max_value:
        bucket_list = [[] for _ in range(num)]  # 创建桶
        for value in lst:
            # ps: 987 i=0:987%10-->7 i=1:987//10%10-->8 i=2:987//100%10-->9
            digit = value // 10 ** i % 10  # 求出当前数的个位、百位、千位...
            bucket_list[digit].append(value)
        lst.clear()
        for li in bucket_list:
            lst.extend(li)
        i += 1
lst = [random.randrange(1, 999) for i in range(10)]
print(lst)
radix_sort(lst)
print(lst)

总结

算法有哪些需要注意的问题

边界问题：0、-1、[]

查找排序相关面试题

给两个字符串s和t，判断t是否为s的重新排列后组成的单词

s = "anagram", t = "nagaram", return true.

s = "rat", t = "car", return false.

"""
给两个字符串s和t，判断t是否为s的重新排列后组成的单词
`s = "anagram", t = "nagaram", return true.`
`s = "rat", t = "car", return false.`
"""
# 方法一
def rearrange(s, t):
    """
    :param s: 第一个字符串
    :param t: 第二个字符串
    :return: True or False
    """
    tmp_dic = {}
    flag = True
    for val in s:
        tmp_dic[val] = tmp_dic.get(val, 0) + 1
    for val in t:
        ret = tmp_dic.get(val, -1)
        if ret == -1:
            flag = False
            break
        tmp_dic[val] -= 1
        if tmp_dic[val] == 0:
            tmp_dic.pop(val)
    if bool(tmp_dic):
        return False
    return flag
# 方法二（排序）
def rearrange(s, t):
    """
    :param s: 第一个字符串
    :param t: 第二个字符串
    :return: True or False
    将两个字符串排好序，如果排完序的字符串相等，就返回True
    """
    return sorted(list(s)) == sorted(list(t))
# 方法三
def rearrange(s, t):
    """
    :param s: 第一个字符串
    :param t: 第二个字符串
    :return: True or False
    用两个字典保存字符串中的字符数量，如果两个字符串的字符数量相同，就返回True
    """
    tmp_dic1 = {}
    tmp_dic2 = {}
    for val in s:
        tmp_dic1[val] = tmp_dic1.get(val, 0) + 1
    for val in t:
        tmp_dic2[val] = tmp_dic2.get(val, 0) + 1
    return tmp_dic1 == tmp_dic2
print(rearrange("anagram", "nagaram"))
print(rearrange("rat", "car"))

给定⼀个m*n的⼆维列表，查找⼀个数是否存在。列表有下列特性：

每⼀⾏的列表从左到右已经排序好。

每⼀⾏第⼀个数⽐上⼀⾏最后⼀个数⼤。

"""
给定⼀个m*n的⼆维列表，查找⼀个数是否存在。列表有下列特性：
每⼀⾏的列表从左到右已经排序好。
每⼀⾏第⼀个数⽐上⼀⾏最后⼀个数⼤。
"""
# 方法一
def find_num(nums, target):
    """
    :param nums: 二维列表
    :param target: 目标数字
    :return: 存在返回True，反之返回False
    """
    tmp_list = []
    for li in nums:
        tmp_list.extend(li)
    # print(tmp_list)  # [2, 9, 11, 13, 15, 27, 56, 78, 97, 100, 112, 130]
    low = 0
    high = len(tmp_list) - 1
    while low <= high:
        mid = (low + high) // 2
        if target < tmp_list[mid]:
            high = mid - 1
        elif target > tmp_list[mid]:
            low = mid + 1
        else:
            return True
    return False
# 方法二
def find_num(nums, target):
    """
    :param nums: 二维列表
    :param target: 目标数字
    :return: 存在返回True，反之返回False
    """
    h = len(nums)  # 行数
    if h == 0:
        return False
    w = len(nums[0])  # 列数
    if w == 0:
        return False
    left = 0
    right = h * w - 1
    while left <= right:
        mid = (left + right) // 2
        # 确定当前数的位置
        i = mid // w  # 行
        j = mid % w  # 列
        if target < nums[i][j]:
            right = mid - 1
        elif target > nums[i][j]:
            left = mid + 1
        else:
            return True
    return False
result = find_num(
    [
        [2, 9, 11],
        [13, 15, 27],
        [56, 78, 97],
        [100, 112, 130],
    ],
    78
)
print(result)
result = find_num([], 78)
print(result)

给定⼀个列表和⼀个整数，设计算法找到两个数的下标，使得两个数之和为给定的整数。保证肯定仅有⼀个结果。

例如，列表[1,2,5,4]与⽬标整数3，1+2=3，结果为[0, 1].

"""两数之和等于所给定的数"""
# 方法一
def twoSum(nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: List[int]
    执行耗时:3584 ms,击败了7.15% 的Python用户
	内存消耗:13.6 MB,击败了84.58% 的Python用户
    """
    for i in range(len(nums)):
        j = i + 1
        while j <= len(nums) - 1:
            if nums[i] + nums[j] == target:
                return [i, j]
            j += 1
# 方法二
def twoSum(nums, target):
    """
    :type nums: List[int]
    :type target: int
    :rtype: List[int]
    执行耗时:268 ms,击败了65.69% 的Python用户
	内存消耗:13.4 MB,击败了97.51% 的Python用户
    """
    i = 0
    j = len(nums) - 1
    while i < j:
        while i < j:
            if nums[i] + nums[j] == target:
                return [i, j]
            i += 1
        j -= 1
        i = 0
print(twoSum([3, 3, 2], 6))
print(twoSum([3, 2, 3], 6))
print(twoSum([3, 2, 4], 6))

posted @ 2023-04-30 20:03 hkwJsxl 阅读(54) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

hankewei cnblogs

学编程的，你得nb

算法入门

算法介绍

时间复杂度

简单总结

如何简单快速地判断算法复杂度

空间复杂度

递归

递归实例：汉诺塔问题

python程序实现

列表查找

查找

顺序查找 (Linear Search)

python程序实现

二分查找 (Binary Search)

python程序实现

列表排序

常⻅排序算法

冒泡排序 (Bubble Sort)

python程序实现

冒泡排序-优化

python程序实现

选择排序 (Select Sort)

python程序实现

直接插入排序

python程序实现

折半插入排序

快速排序

python程序实现

堆排序

堆排序前传-树与二伹树

堆排序前传-二叉树

堆排序前传-完全二伹树

堆排序前传-二叉树的存储方式

二叉树的顺序存储方式

堆排序-什么是堆

堆排序-堆的向下调整性质

堆排序过程

python代码实现

堆排序-内置模块

堆排序-topk问题

归并排序

python代码实现

NB三人组小结

希尔排序

python代码实现

计数排序

python代码实现

桶排序

桶排序-复杂度

python代码实现

基数排序

python代码实现

总结

算法有哪些需要注意的问题

查找排序相关面试题

公告