网络流

简述

网络流主要可以拿来解决一些跟有向关系相关的问题，例如液体在管道中的流动、货物的运载、网络中的信息波动等。
简单介绍一下它：在一个有向图上选择一个源点s、一个汇点t。源点只流出，汇点只流进。同时，一条边$(u,v)$经过的流量记为$f(u,v)$,也有允许通过的最大流量称为容量,记为$c(u,v)$。（若该边不存在，则$c(u,v)=0$）。除了源点和汇点以外的每个店入流和出流都相等。一条边上的剩余流量（没有用完的）称为残量，即 容量-流量。
因此网络流模型可以形象地描述为：在每一条边都不超过容量限制的前提下，“流”从源点源源不断地产生，最终全部归于汇点。

基本性质

1. $f(u,v)\le c(u,v)$（容量限制）
2. 对于任何一个不是源点或汇点的点$\text{u}$,总有 $\sum_{p\in E}f(p,u)=\sum_{q\in E}f(u,q)$
   因为入流和出流相等（流量平衡）
3. 对于任何一条有向边$(u,v)$,总有$f(u,v)=-f(v,u)$ （斜对称性）

最大流

先讲一下比较简单的最大流问题。
直接从字面意思即可理解，从源点流到汇点的流量最大就是最大流。

算法思想：从零流（所有边的流量均为0）开始不断增加流量，保持每次增加流量后都满足以上性质（增加流量，也就是减去容量时要相应的给反向边加上等量的容量，便于反悔）。计算每条边上的残量，得到残量网络，再继续在残量网络中尝试增加流量。

增广路算法基于：残量网络中任何一条从$s$到$t$的有向道路都对应一条原图中的增广路——只要求出该道路中所有容量的最小值$minf$，把对应的所有边上的流量减去$minf$，在答案里加上它即可，这个过程被称为增广。
显然只要残量网络中存在增广路，流量就可以增大；反之，如果不存在增广路，流量就已经最大。（增广路定理）

顺便也讲一下最大流最小割定理。

最小割

• 割：对于一个网络流图$G=(V,E)$，其割的定义为一种点的划分方式：将所有的点划分为$S$和$T=V-S$两个集合，其中源点$s\in S$，汇点$t\in T$。
• 割的容量：定义割的容量$c(S,T)$表示所有从$S$到$T$的边的容量之和，即$c(S,T)=\sum_{u\in S,v\in T}c(u,v)$。当然也可以用$c(s,t)$表示割的容量。
• 最小割：使得容量最小的割$(S,T)$。也可以理解为使得$S$和$T$不联通所需要删去边权最小的割。

最大流最小割

• 定理：$f(s,t)_{max}=c(s,t)_{min}$
• 证明：对于任意一个可行流$f(s,t)$和任意割$(S,T)$，有：$f(s,t)=S_\text{出边的总流量}-S_\text{入边的总流量}\le S_\text{出边的总流量}=c(s,t)$。而当达到最大流时，残量网络中不存在从$s$到$t$的增广路，所以$S$的出边都是满流，上式等号成立。同时，上式的另一表达形式为$f(s,t)_{max}\le c(s,t)_{min}$。又因等号可以取到，则$f(s,t)_{max}=c(s,t)_{min}$，证毕。

问题模型

一般在最小割的问题中，割掉一条边表示选择某个条件，而边权表示的是选择这个条件的价值。至于该价值的贡献是好是坏，则根据你如何使用这个价值而定。

举个例子，对于二分图，有点集$U,V$。$\forall e=(u,v) (u\in U,v\in V)$表示u、v中至少选择一个，保证无孤立点，求最小点权覆盖集。

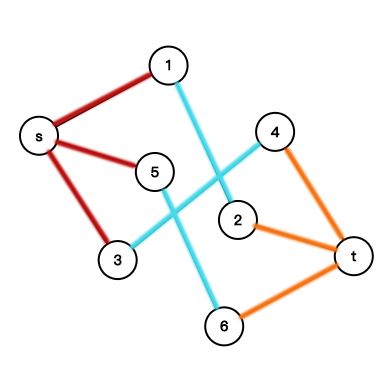
设左边为点集$U$，右边为点集$V$，如图所示连边。割掉红色边表示选择$U$中某个点，其点权设为$val_u$；割掉蓝色边表示选择该边两端的点，其点权设为$val_u+val_v$；割掉橙色边表示选择$V$中某个点，边权设为$val_v$。这样一来，若一条边不从$s$连通到$t$，则表示至少有一个点被选中，求得的最小割即为最小点权之和，覆盖集可通过边的使用情况求得。
事实上，我们都清楚，为了使点权之和最小化，蓝色的边是不会被割掉的。而仍然要设置它的原因，一是为了结合问题背景来建模，二是让它承担通道的角色，保证网络流图的性质。问题建模是非常值得琢磨的。

如果转换一下，边的限制变成u、v中至多选一个，求最大点权独立集。其本质相同，因为至多选一个等价于至少删去一个。由此可以看出，最大点权独立集为最小点权覆盖集的补集，其解法自然也就不言而喻了。

这里只是提供了一个参考的思路，具体的问题还要具体分析。

最小割的边数

将边权设为1重新求一遍最小割即可。

最小割集的求解

由于使用网络流解决此类问题效率较为低下，普遍使用$\texttt{Stoer-Wagner}$算法进行求解，有兴趣可自行查阅。

一些小细节

• 存图的时候要从偶数开始存，同时存正向边和反向边（这样就可以保证正向边编号全为偶数，反向边编号为 i^1（奇偶性相反））

• 反向边怎么用？因为找到的增广路不一定是最优的，反边给你“反悔”的机会。如果一条边边权为0，那么往回走的时候并不会对流量有所影响（走不回去）。所以一开始反边的边权应该存0。当正向边减去流过这条边的增广路上容量最小值d（此时这个值已经被加入到了答案）的时候，反向边应该加上d（因为对于源点和汇点来说中间流量的这些变化都是无差别的，为了保证反向正向相加得原边权，也就是不改变原本的条件就得这么做）

Edmonds-Karp(EK) 便是不断用$\texttt{BFS}$来寻找增广路，直到图中不存在增广路的算法。

但是如果一条一条地找出增广路，万一有一些极（毒）端（瘤）数据（比如几条相邻的边容量相差特别大），这个时间复杂度就是无法承受的。Dinic的高效之处在于它能够同时找出几条增广路.

关于最大流，我还没有讲完！当然，实际上在大部分情况下以上两个算法已经够用（我认为）。可以先跳过剩下有关最大流的算法。

（这里应该有ISAP和HLPP）

最大流/最小割 练习题

USACO4.2 草地排水

飞行员配对方案问题

USACO4.4 追查坏牛奶

圆桌问题

最小路径覆盖问题

魔术球问题

最长不下降子序列问题

方格取数问题

费用流

假如流经一条边有对应流量的花费，那么问题就可以有更多的变式了。

• 定义一条边的费用$w(u,v)$表示单位流量流经所需花费的费用。即，当边$(u,v)$的流量为$f(u,v)$时，需要花费$f(u,v)\times w(u,v)$的费用。

类似的，我们先从最小费用最大流引入。即在最大化流量的基础上使得总花费最小。
这当然和上面的最大流相关。之前寻找增广路的方式是$\texttt{BFS}$，对于$\texttt{EK}$来说，就是在边权为1的图上找到$s\rightarrow t$的一条最短路。那么，将 $\texttt{BFS}$ 更换为寻找最短路的算法，边权设为$w(u,v)$，会产生什么样的效果呢？

这样的方式，既保证了最短路的性质，也保证了增广路的性质。由于每单位流到汇点的流量都要花费途经的边权之和，则最短路的性质使得了这些每次从最短路流过的流量是最划算的。在这样的情境下，反向边相当于退钱，所以要将边权设为$-w(u,v)$。

而 $\texttt{Dinic}$ 是同时找到多条增广路的算法，只需将 $\texttt{BFS}$ 更改为最短路算法的同时，限制流量只能由当前点流向到汇点的最短路上的点即可。

因为有负权边的存在，所以不能直接采用 $\texttt{Dijkstra}$ ，应该采用 $\texttt{SPFA}$ 或经由 $\texttt{Primal-Dual（原始对偶算法）}$ 处理的 $\texttt{Dijkstra}$ 。同时，由于向下走的条件发生改变，有可能会往回走，所以需要标记当前链上的点，防止陷入无限循环。

上下界网络流

无源汇上下界可行流

给定一个网络无源点汇点，且每条边的流量有上限$high$和下限$low$，问使得该网络流量平衡的一种流量方案。
没有源汇点意味着流一定要形成循环，否则不满足流量平衡的条件。
不妨假设有解，先将所有的下界强制流满（不考虑流量平衡的情况），然后考虑如何调整使得流量平衡。
设超级源点$ss$，超级汇点$st$。对于每条边$e=(u, v, high, low)$，添加$u$至$st$和$ss$至$v$容量为$low$的边，将$(u,v)$的容量设为$high-low$。
把$low$从$u$处导走，并在$v$处加回便是一个强制流满下界的操作，同时不会影响到原本的网络；$(u,v)$的流量设为$high-low$是为了限制流量的上界。
接下来跑一遍从$ss$到$st$的最大流，若能把所有附加的边全部跑满，则说明在满足上界限制的情况下所有的下界限制均被满足，合法方案即为每条边下界流量加上跑完这遍网络流之后所用的流量；否则无解。
一个小优化是，两个点之间无下界无费用的流可以合并。

无源汇上下界最小费用流

将后面那个最大流改成最小费用最大流即可。

有源汇上下界可行流

添加一条由汇点$t$到$s$的下界为0，上界为正无穷的边即可转化为无源汇上下界可行流。
若有解，$s$到$t$的可行流流量即为该附加边所流的流量。

有源汇上下界最大流

一种方法是二分$t$到$s$的附加边的下界，然后跑普通可行流判断合法性。
另一种方法是先附加一条无下界的正无穷的边，变成无源汇跑一遍可行流之后若存在合法方案便将其删去，在剩余的网络中跑一遍从$s$到$t$的普通最大流，答案为可行流的流量加上最大流得到的流量。这个也很好理解，先跑一遍可行流满足下界，之后在上界的限制下继续尝试增广得到实际的最大流。
*注意：最大流是在跑完可行流的网络上跑，不要跑到初始网络上。

有源汇上下界最小流

一种是二分$t$到$s$的附加边的上界，然后跑普通可行流判断合法性。
另一种方法是先附加一条无下界的正无穷的边，变成无源汇跑一遍可行流之后若存在合法方案便将其删去，在剩余的网络中跑一遍从$t$到$s$的普通最大流，答案为可行流的流量减去最大流得到的流量。简单来说，就是先找到可行的方案，再把能退回去的流都退回去。
注意事项同上。

参考

• EK不够快？ 再学个Dinic吧 by 钱逸凡
• Dinic算法 by SYCstudio
• 从入门到精通：最小费用流的“zkw”算法 by zkw
• 基于 Capacity Scaling 的弱多项式复杂度最小费用流算法 by ouuan
• OI Wiki
• 《算法竞赛入门经典第二版》
• 《算法竞赛进阶指南》
• 《算法导论》