AC自动机
AC自动机利用trie树可以高效解决有关多个字符串的问题。
Trie树
也称字典树,它的本质是使得字符串集合\(S\)构成一棵树,其中边权记录字符信息。
它的根到任意节点的路径对应集合\(S\)中某一字符串的前缀。
任意节点向深度增大的方向经过的路径对应\(S\)中某一字符串的子串。
比如下面这一棵\(\text{trie}\),就记录了\(\text{why,who,when}\)这几个字符串所构成的集合的信息:
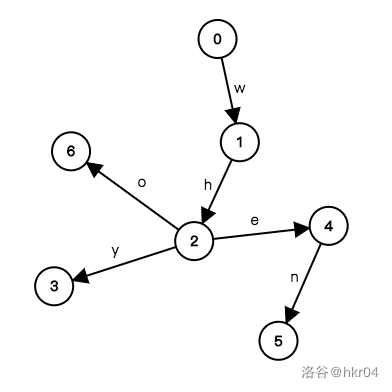
简单来说,\(\text{trie}\)的插入是这样的:
- 从根节点进入,从插入的字符串的首位开始考虑,若属于这位字符的边走向的点已存在,就继续往下走;否则,就为这条边创建一个新的节点;
- 向下走后重复以上过程;
- 直到走完所有字符,最后所处的位置进行标记,表明从根节点到这的路径属于集合中。
int tot=0;
void insert(char *s,int l_s)
{
int p=0;
for (int i=1;i<=l_s;i++)
{
if (!trie[p][s[i]-'a'])
trie[p][s[i]-'a']=++tot;
p=trie[p][s[i]-'a'];
}
end[p]++;
}
关于trie树的定义
- 状态:从根节点到任何一个字典树上的节点的路径表示的字符串都代表着一个状态
- 转移:任意一个状态添加一个新的字符得到新状态
- 可识别:若一个字符串能对应字典树上的某一状态,则称其为可识别
- 标记状态:特指属于集合S的状态
查询字符串\(s\)是否在集合中\(\rightarrow\)在\(\text{trie}\)上遍历,在结尾处查询是否有相应状态(遍历与插入的过程类似)
查询是否有字符串\(s\)的某个前缀在集合中\(\rightarrow\)遍历的时候每经过一个节点就检查一遍是否为标记状态
查询是否有字符串\(s\)的某个子串在集合中\(\rightarrow\)因为子串都是某个前缀的后缀,所以只需查询\(s\)的每个前缀有多少可识别并被标记的后缀
一般敏感词屏蔽就可以用这样的方法,不过有可能会误伤一些连起来的正常词语。
下面我们来解决查询是否有字符串\(s\)的某个子串在集合中的这个问题
我们定义\(\text{fail[s[1..i]]}\)表示\(\text{s[1..i]}\)的最长可识别后缀(你可以将它理解为一个字符串指针,虽然实际上我们会用数组实现,使它指向一个状态的编号)。容易发现的是,可识别后缀具有传递性,即:若\(s\)是\(t\)的可识别后缀,\(t\)是\(r\)的可识别后缀,则\(s\)也为\(r\)的可识别后缀.
依据这个性质,设\(\text{s[1..i]}\) \(=t\),其所有可识别后缀为\(\text{fail[t],fail[fail[t]],fail[fail[fail[t]]]}\) \(\cdots\),且长度递减。
那么,怎么处理这个\(\text{fail}\)指针呢?
假设有字符串\(x\),\(\text{fail[x]=y}\).考虑\(x\)加上一个字符\(c\)后的新字符串\(xc\)的\(\text{fail}\)指针。显然,\(xc\)的可识别后缀必然为\(x\)的某个可识别后缀加上\(c\)的形式。所以,我们为了求出\(xc\)的最长可识别后缀,只需查询\(\text{yc,fail[y]c,fail[fail[y]]c}\) \(\cdots\)中最长的可识别串即可.
接下来考虑依赖关系。由上,我们知道想要一个字符串的\(\text{fail}\)指针与比其长度少一的可识别后缀有关,长度在\(\text{trie}\)树上的表现即为深度。所以,我们应按照深度从小到大计算每个节点所代表的状态的\(\text{fail}\)指针。可用\(\text{BFS}\)实现。
建立AC自动机伪代码:
\(build\ trie\ T\ from\ S=\left\{str_1,str_2...\right\}\)
\(sort\ every\ state\ in\ T\ by\ depth\)
\(fail[root]=\phi\)
\(for\ each\ c,trans(\phi, c)=root\ (to\ avoid\ some\ error)\)
\(for\ state\ x\ in\ T\)
\(\ \ \ \ \ \ for\ xc\ in\ T\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ y=fail[x]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ while \ y\neq\phi\ and \ yc\ not\ in\ T\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ y=fail[y]\)
\(\ \ \ \ \ \ \ \ \ \ \ \ \ fail[xc]=yc\)
注意到,当新加进来字符的状态不能直接被当前的\(fail\)匹配时,需要一直在\(fail\)链上跳,直到能扩展匹配或跳到空集。有一个小优化可以在我们不需要访问或更改\(\text{trie}\)树的信息使用:若\(yc\)不存在,则将其直接指向\(fail[y]c\)。这样以来,就可以避免多余的跳动,直接指到最长可匹配的状态。
结合代码理解:
void build()
{
for (int i=0;i<26;i++)
if (trie[0][i])
{
fail[trie[0][i]]=0;
q.push(trie[0][i]);
}
while(!q.empty())//借助队列依照深度从小到大的关系对状态进行更新
{
int u=q.front();
q.pop();
for (int i=0;i<26;i++)
{
if (trie[u][i])
{
fail[trie[u][i]]=trie[fail[u]][i];//不需要考虑是否真的有对应状态,若有,直接匹配;若没有,得到之前深度最大的匹配
q.push(trie[u][i]);//继续更新深度更大的状态
}
else
trie[u][i]=trie[fail[u]][i];//相当于一个虚点,指向它相当于指向前一个点,这是一个传递的关系,减少了尝试匹配的操作
}
}
}
接下来,求\(s\)被\(S\)中的字符串匹配的次数只需在于AC自动机上遍历\(s\)的过程中求出每个状态\(fail\)链上的标记数即可。需要注意的是,如果我们要求的是有多少个字符串出现在s中,那么每个标记状态应只被记录一次。为避免重复记录,应将访问过的标记状态的贡献记为-1,就像这样:
int solve(char *s,int l)
{
int u=0,ans=0;
for (int i=1;i<=l;i++)
{
u=trie[u][s[i]-'a'];
for (int t=u;t&&end[t]!=-1;t=fail[t])//由于fail的传递性,fail链上的状态应是连续的被访问过再到未被访问过
ans+=end[t],end[t]=-1;
}
return ans;
}
如果我想要知道所有字符串分别被匹配的总次数呢?改变一下状态的记录方式,把每个字符串的终点编号记录下来,每次访问到该状态就将这个次数加1。这是非常直观的想法,但是想想我们求解\(fail\)的过程,往上跳真的很需要时间!接下来好好想想,怎么样才能避免那么多的跳跃?
由于\(fail\)是具有唯一前驱状态的,这符合一棵树的形态,其根节点为空集。当我们访问某一个节点,其到根的链上的节点都被访问一次。所以,为了避免每次都通过跳跃来更新信息,我们应该在每次第一个访问的节点上打上标记,当所有标记都打完之后自底向上地更新信息。可以用拓扑排序,也可以\(\text{dfs}\)回溯时更新信息,方法多样。




