数据结构实验代码分享 - 4 （迷宫与栈）

迷宫与栈问题（图的应用）

【问题描述】

以一个 m*n 的长方阵表示迷宫，0 和 1 分别表示迷宫中的通路和障碍。设计一个程序，

对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

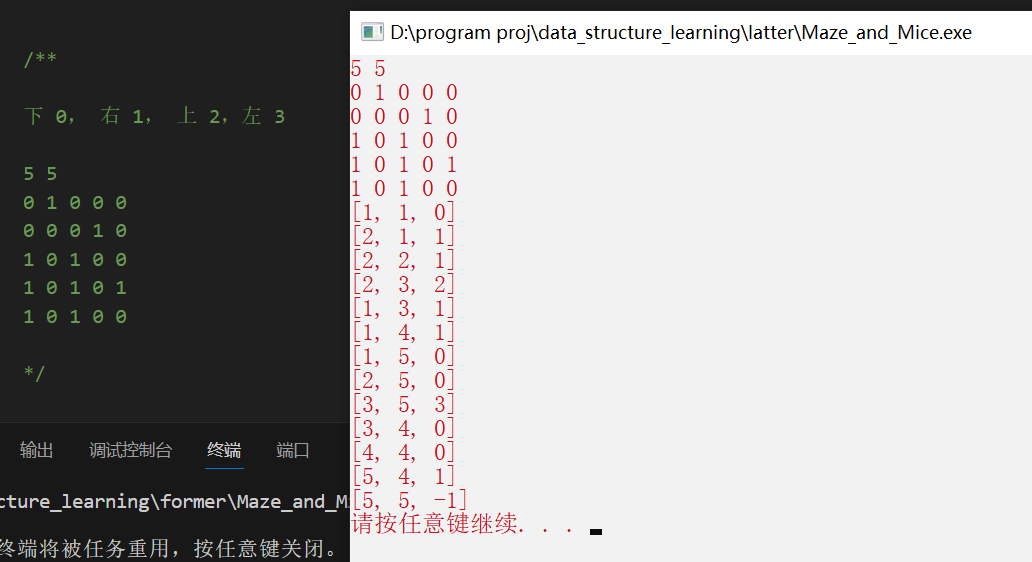
输入：行 列

迷宫，0表示无障碍，1表示有障碍

输出：一条Path 或 “NO PATH”

 

注：参考了《数据结构算法与应用 C++语言描述》

设计思路

这题不算难，直接应用DFS及其思想探出一条路来即可，有路就返回true，否则返回false；

自顶向下分析：

1. 存储输入的迷宫（CreateMaze()）；
2. 找路（FindPath()）；
3. 有路就输出路径，没有就输出“ NO PATH! ”。

 

一些细节：

　　1. DFS的两个要点在于状态记录栈 + 已访问标记List

a)       每当DFS访问到某点，即将那个点置为“障碍”，作为DFS的已访问标识

b)      状态记录栈可以用递归的系统工作栈，也可以自己写个栈

　　2. 迷宫外层包一圈“障碍”，以统一迷宫内外层的操作

 

代码实现

// 找到迷宫路径 (DFS + 栈)  : 下 0， 右 1， 上 2，左 3
bool findPath(vector<vector<bool>> &arr, vector<position> &Path) {
    const position exit(arr.size() - 2, arr[0].size() - 2); // 出口
    position curr(1, 1);
    int r = curr.row, c = curr.column;   // 当前行列索引
    do {
        curr.row = r; curr.column = c; // 更新当前节点值
        arr[curr.row][curr.column] = true; // DFS已访问标记

        Path.push_back(curr);
        curr.option = -1;
        // 此处判断是否到达出口，如果到达直接return true
        if(IsExit(curr, exit)) {
            return true;
        }
        // 没到达出口则继续移动
        while(CouldMove(arr, curr.row, curr.column) == false) {
            if(Path.size() == 0) {
                return false;   // 若栈退到栈空，则全路径再无可移动方向，即全是死路
            } else {
                Path.pop_back();    // 若栈不空，则退栈，直至某位置尚有移动方向
                if (Path.size() > 0) {
                    curr = Path[Path.size() - 1];   // 更新当前结点
                }
            }
        }
        // 更新当前行列索引
        r = curr.row;
        c = curr.column;

        // 下一步往哪走？
        whereToGo(arr, Path, r, c);

    } while (Path.size() != 0); // 结束条件：到达出口 或 Path栈空

    return true;
}

 

运行结果