自顶向下
这是一个解决复杂问题行之有效的设计方法,基本思想是以一个问题开始,试图把它表达为很多小问题组成的解决方案。
现在我做一个有关于乒乓球赛的预测结果的程序:
乒乓球赛的比赛规则:
在一局比赛中,先得11分得一方为胜方;10平后,先多得2分得一方为胜方。
输入代码:
from random import random def printIntro(): print("兵乓球比赛结果预测") print("作者:花椒🐟") print("这个程序模拟两个选手A和B的乒乓球比赛") print("程序运行需要A和B的能力值(以0到1之间的小数表示)") def getInputs(): a = eval(input("请输入选手A的能力值(0-1): ")) b = eval(input("请输入选手B的能力值(0-1): ")) x = eval(input("模拟比赛的场次: ")) return a, b, x def simNGames(x, probA, probB): winsA, winsB = 0, 0 for i in range(x): scoreA, scoreB = simOneGame(probA, probB) print(scoreA,scoreB) if scoreA > scoreB: winsA += 1 else: winsB += 1 return winsA, winsB def simOneGame(probA, probB): scoreA, scoreB = 0, 0 serving = "A" while not gameOver(scoreA, scoreB): if serving == "A": if random() < probA: scoreA += 1 else: serving="B" else: if random() < probB: scoreB += 1 else: serving="A" return scoreA, scoreB def gameOver(a,b): if (a>=11 and abs(a-b)>=2) or (b>=11 and abs(a-b)>=2): return True def printSummary(winsA, winsB): x = winsA + winsB print("竞技分析开始,共模拟{}场比赛".format(x)) print("选手A获胜{}场比赛,占比{:0.1%}".format(winsA, winsA/x)) print("选手B获胜{}场比赛,占比{:0.1%}".format(winsB, winsB/x)) def main(): printIntro() probA, probB, x = getInputs() winsA, winsB = simNGames(x, probA, probB) printSummary(winsA, winsB) main()
各输入两位选手的实力,得到结果为:
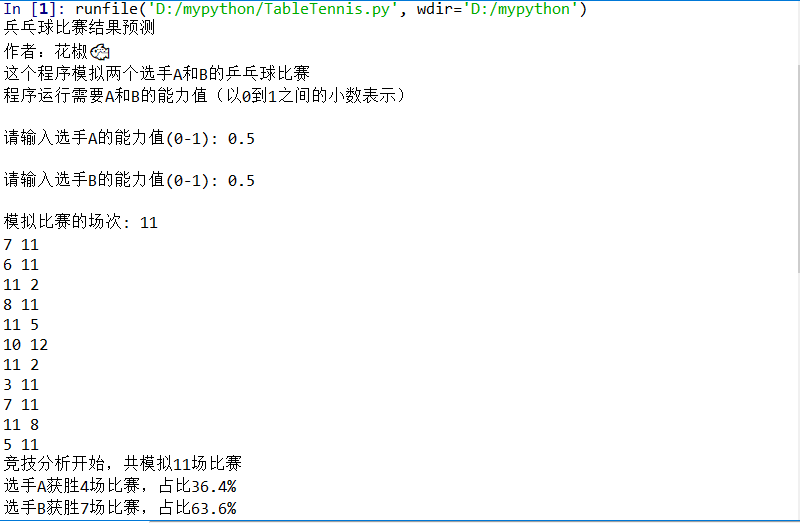
乒乓球单打赛制是七局四胜,双打是五局三胜。再一次运行代码,得到结果:
单打:

双打:

这就是简单的乒乓球比赛结果预测





