Python之进度条及π的计算
文本进度条
1. 简单的开始
这是利用print()函数来实现简单的非刷新文本进度条。它的基本思想是按照任务执行百分比将整个任务划分为100个单位,每执行N%输出一次进度条。
为了模拟任务处理的时间效果,需要调用Python标准时间库time。
完整代码如下:
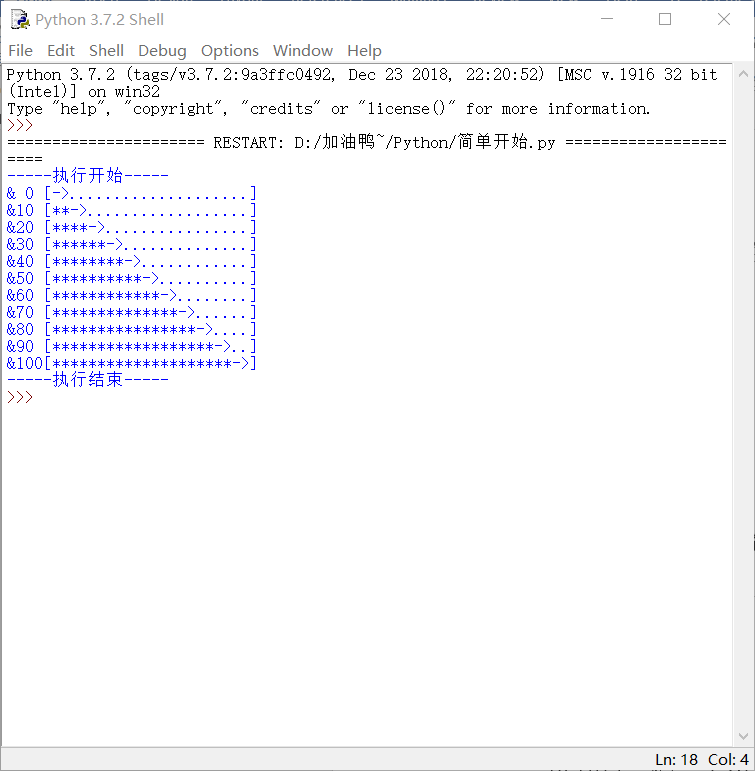
import time scale=10 print("-----执行开始-----") for i in range(scale+1): a,b='**'*i,'..'*(scale-i) c=(i/scale)*100 print("&{:^3.0f}[{}->{}]".format(c,a,b)) time.sleep(0.1) print("-----执行结束-----")
执行效果如下:
2. 单行动态刷新
此进度条相比第一类,区别在于原地输出和动态刷新。它的基本思想是将每一次进度输出都固定在同一行,并不断地用生成的字符串覆盖之前的输出,形成进度条不断刷新的动态效果。
完整代码如下:
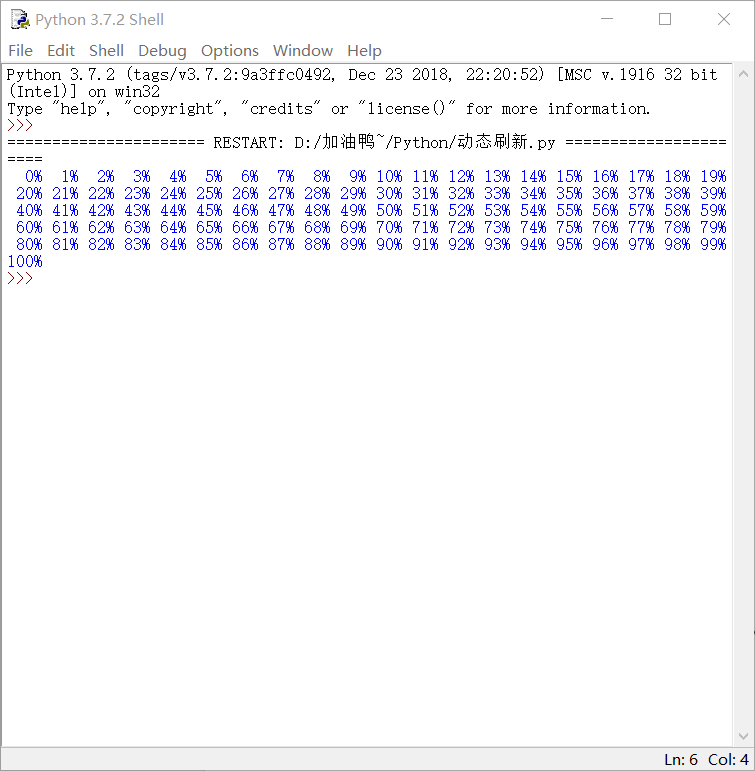
import time for i in range(101): print("\r{:3}%".format(i),end="") time.sleep(0.05)
执行效果如下:
3. 带刷新的文本进度条
为了更好地实现带刷新的文本进度条,我们可以将前两个程序进行合并,在为其添加开始和结束提示语。这里需要调用time.clock()函数,主要用来统计程序运行时间,以达到更好的体验效果。
完整代码如下:
import time scale=50 print("执行开始".center(scale//2,'-')) t=time.clock() for i in range(scale+1): a='*'*1 b='.'*(scale-i) c=(i/scale)*100 t=time.clock() print("\r{:^3.0f}%[{}->{}]{:.2f}s".format(c,a,b,-t),end='') time.sleep(0.05) print("\n") print("\n"+"执行结束".center(scale//2,'-'))
执行效果如下:
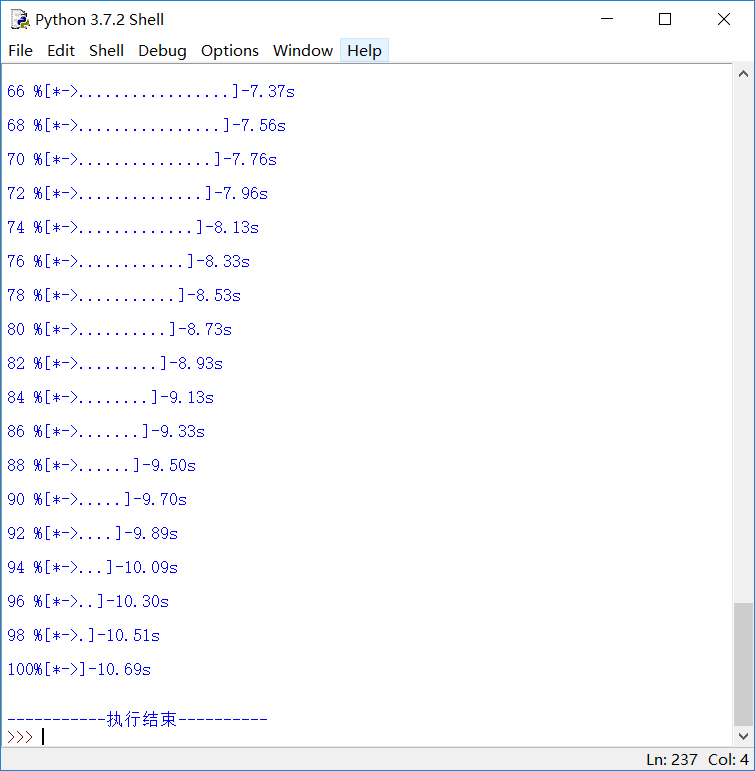
以上便是文本进度条的操作。
π的计算
对π的精确求解曾经是数学历史上一直难以解决的问题之一,直到1948年,人类以人工计算方式得到π的808位精确小数。
计算π的方法有许多种,现在我介绍其中一种求π的方法——蒙特卡罗法。
蒙特卡罗方法求解π的基本步骤:随机向的单位正方形和圆结构,抛洒大量“飞镖”点,计算每个点到圆心的距离从而判断该店在圆内或圆外,用圆内的点书除以总点数就是π/4值。
实际上其思想是利用离散点值表示面积,通过面积比例来求解π值。(随机点数量越大,越充分覆盖整个图形,计算得到的π值越精确)
因为计算圆周率的程序需要时间运行,我们可以用进度条来提示程序的完成度。
完整代码如下:
from random import random from math import sqrt from time import * DARTS=10000000 hits=0.0 for i in range(1,DARTS+1): x,y=random(),random() dist=sqrt(x**2+y**2) if dist <=1.0: hits=hits+1 pi=4*(hits/DARTS) for i in range(101): print("\r{:3}%".format(i),end="") sleep(0.01) print("pi的值{}.".format(pi)) print("运行时间:{:.5f}s".format(clock()))
运行结果如下:
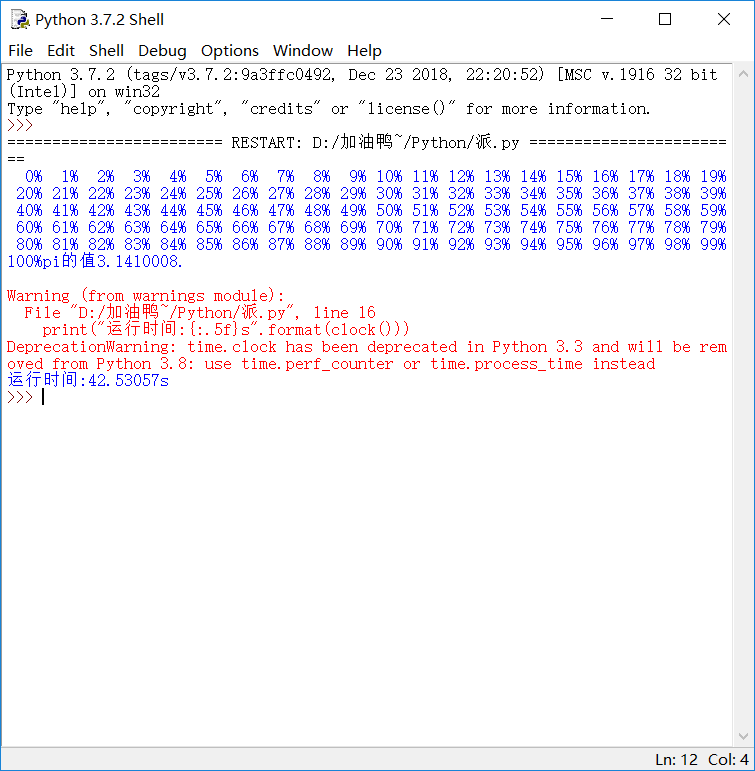
这就是蒙特卡罗法求解圆周率。



