密码学——密码学基础、散列函数与数字签名
1.密码学概述
是信息安全的基础和核心,是防范各种安全威胁的重要手段,信息安全的许多相关知识都与密码学相关。
密码学发展
密码学是一门古老而又年轻的学科 ,几千年以前就存在,至今仍在发展演进。地位非常重要甚至起决定性作用。密码学源于希腊语kryptós,意为“隐藏的” 。 最早的密码学应用可追溯到公元前2000年古埃 及人使用的象形文字。
历史上的第一件军用密码装置是公元前5世纪的斯巴达密码棒它采用了密码学上的移位法(Transposition)原理。发送方把兽皮缠在一根木棍上,在上面写字,写完字后把兽皮解下来,别人看不懂上面写的内容,接收方只要有一根差不多一样的木棒,把兽皮缠在密码棒上就能还原之前写的内容。
用途:保护军事通讯安全
恺撒大帝发明了最早的实用代替密码方案(尤利 西斯.恺撒100-44 BC)把要发送的消息中的每个字母,根据代替表,替换成对应的字母 。
作用:保护机密通信 用途:保护军事通讯安全
例如:
this is caesar code
vjku ku ecguct eqfg
a b c d e f g h i j k l m n o p q r … x y z
c d e f g h i j k l m n o p q r s t … z a b
二战期间,日本采用M-209转轮机械加密机—紫密,这种加密方式,手工计算短时间无法破解。此时美国已经研制出计算机,1943年,通过解密通信内容获悉山本五十六将于4月18日乘中型轰炸机,由6架战斗机护航,到中途岛视察时,罗斯福总统下令拦截,山本坠机身亡,日本海军从此一蹶不振。
德国采用的enigmam(谜语)密码机被盟军破译,对于扭转二战局面起到了重要作用。只有字母键,可以可输入的字母直接转化为密文,事先要约定好转子作为密钥。
密码学流派
密码学是在编码与破译的斗争实践中逐步发展起来的, 伴随着编码和破译之间的较量不断发展。
编码密码学:编制密码以保护通信秘密的,称为编码密码学 如:enigmam
密码分析学(或破译密码学):破译密码以获取通信情报的。
发展阶段
第一阶段:古代—1949年 ,密码技术可以说是一种艺术,而不是一种科学, 密码学者常常是凭直觉来进行密码设计和分析, 而不是推理和证明。 在现代计算机技术条件下都是不安全的 ,但是算法思想(代换、置换)是分组密码算法的基本运算模式。
第二阶段:1949年—1975年 ,1949年香农发表的<<保密系统的信息理论>>为私钥密码系统建立了理论基础,从此密码学成 为一门科学 。美、苏、英、法等很多国家已经意识到了密码的重要性,开始投入大量的人力和物力进行相 关的研究,研究成果都是保密的,Enigma的破解过程以及原理都是过 了几十年以后才公布的。
第三阶段:1976年—今 ,1976年Diffie 和 Hellman发表文章“密码学的新动向”开创了公钥密码学的新纪元。是密码学的一场革命。从此,密码开始充分发挥它的 商用价值和社会价值。1978年,Rivest、Shamir和Adleman公布了RSA 密码体制,是第一个真正实用的公钥密码体制,对计算机安全和通信产生巨大影响,发明人因此获得了图灵奖。计算机领域最高奖项。
密码学发展的新方向
量子密码
用目前物理学的知识来开发不能被破解的密码系统,不了解发送的密钥,攻击者无法破解所截获的内容,依赖于物理学作为安全关键,而不是数学上的困难问题。量子密码基于单光子的应用和它固有的量子性质开发出来的不可破解的密码系统。
混沌密码
是新的密码加密算法,简单、高效。混沌密码是混沌理论的一个重要应用领域,混沌理论用于密码学主要依靠混沌的基本特征(随机性、便利性、确定性、和对初始条件的敏感性),混沌密码体系的结构与传统密码理论当中混淆和扩散概念联系起来,混沌理论和纯密码学之间的必然联系形成了混沌的密码学。
DNA密码
由DNA计算产生,主要特点:以DNA作为信息载体,以现代生物学为主要载体来挖掘DNA固有的高存储密度以及高并行性优点从而实现加密、认证、签名等密码学功能。
缺点:缺乏有效的安全理论依据以及简洁的实现方式,目前的研究主要都是基于发觉DNA可用于信息领域的优良性质,探寻DNA密码可能的发展方向,寻找实现DNA密码的简便方法。
基于格的密码体制
抗量子计算攻击的公钥密码体制,格密码理论研究涉及密码数学问题很多,学科交叉特色非常明显,研究方法也基于多元化。发展大概分为两条主线,一种是从具有历史悠久的经典的格的数学问题的研究发展到近30年来高围格困难问题的求解算法以及计算复杂性理论的研究;另一种是使用格困难问题的求解算法,分析非格公钥密码体制的安全性发展到基于格的困难问题的密码体制的设计。
轻量级密码
密码学分支的一个重要领域,它的目标是针对资源受限(这些设备的计算能力不够强或者无法提供复杂的持续的密码运算)的设备,经给定制和裁剪产生的一种密码解决方案。
应用领域:汽车系统、传感器网络、医疗设备、分布式控制、物联网等。
同态密码
同态密码是基于数学难题和计算机复杂性理论的一种密码学技术,对经过同态加密的数据进行处理,可以得到一个输出,这个结果与使用同一方法来处理未加密的原始数据得到的结果可以是一样的即两个数分别加密后在做加法,密文相加之后的结果解密以后跟直接把这两个数做加法的结果是一样的,这样就可以实现密文域上的运算。
应用领域:密文搜索、电子投票、移动代码和多方安全计算、云计算等。
2.密码学基础
密码学基本概念
要传输的消息M叫做明文,(可以是文本文件、位图、 数字化的语言、数字化的视频图像) 。明文通过加密器加密后得到密文C。将明文变成密文的过程叫加密, 一般记为E,它的逆过程称为解密一般记为D
C=E(M), M=D(C)
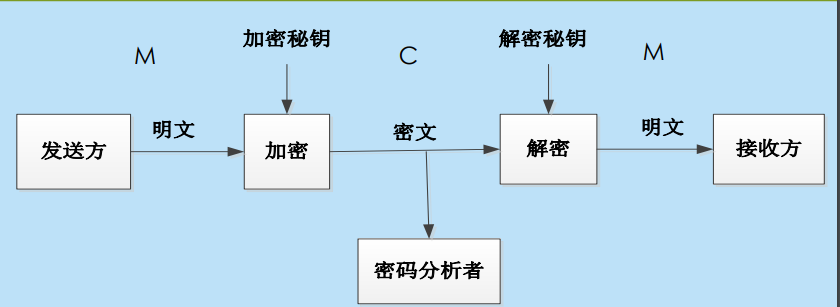
密码体制的分类
根据密钥的特点,密码体制可以分为对称密码体制 (Symmetric Cryptosystem) 和非对称密码体制 (Asymmetric Cryptosystem)两种。 加密、解密使用相同密钥的是对称密码体制,也称单钥(Onekey) 加密、解密使用不同密钥的是非对称密码体制,也称做双钥 (Two-Key) 或公钥(Public Key)密码体制。 加密密钥和解密密钥成对出现,从一个难于推算出另一个 ,一个叫公钥public key,一个叫私钥private key。
对称密码体制中,按照加密方式又可以分为流密码(Stream Cipher)和分组密码 (Block Cipher)两种。在流密码中将明文消息按字符逐个地进行加密,类似于流水线 ;在分组密码中将明文消息进行分组(每组N个字符),逐组地进行加密。
科克霍夫(Kerckhoff)原则 :现代密码学的一个基本原则——密码体制应该对外公开,仅需对密钥进行保密。 在设计加密系统时,总是假设密码算法是公开 的,真正需要保密的是密钥。一个密码系统需要保密的越多,可能的弱点也越多。依据柯克霍夫原则,大多数民用加密系统都使用公开的算法。 但相对地,用于政府或军事机密的加密算法通常是保密的。
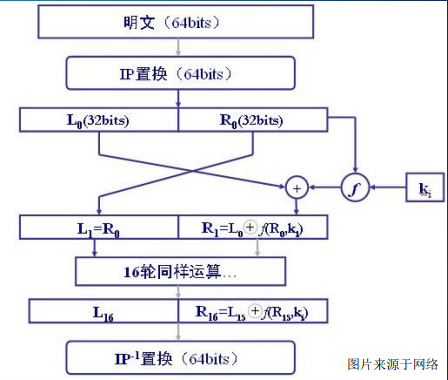
DES加密算法:
在1976年,IBM沃森公司的菲斯特和美国国家安全局 一起制定了DES标准 (Data Encryption Standard) ,DES算法是美国政府机关为了保护信息处理中的计算机数据而使用的一种加密方式,属于对称密码体制,分组密码算法。加密时算法输入64比特的明文,在64比特密钥的控制下产生并输出64比特的密文;解密时输入64比特的密文,在密钥控制下输出64比特的明文分组。
64比特的密钥中含有 8个比特的奇偶校验位,所以实际有效密钥长度为56比特,密钥扩展6轮 ;解密是加密的逆过程 ;在密码学的历史上是 一个具有深远影响的。
64比特明文首先进行初始置换。功能是把输入的64位数据块按位重新组合,并把输出分为L0 、R0两部分, 每部分各长32位,置换规则使用的是置换表。
虽然由于密钥长度的原因,DES安全性已经无法满足现有信息安全要求 ,3DES是DES算法扩展其密钥长度的一种方法,可使加密密钥长度扩展到128比特 (112比特有效)或192比特(168比特有效)。
基本原理:是将192比特的密钥分为64比特的3组,对明文多次进行普通的DES加解密操作 ,比如用第1组密钥对明文进行DES加密,用第2组密钥对其结果进行DES解密,(第一组、第二组加密、解密使用的密钥不同)再使用第3组密钥对解密结果进行DES加密 ,解密过程还是逆过程。
RSA加密算法:
迄今为止的所有公钥密码体系中,RSA系统是最著名、使用最广泛的一种。RSA属于非对称密码体制。 是由R. Rivest、A. Shamir和L. Adleman三位教授提出的。
基本原理:密钥中心先产生两个足够大的强质数p、q,然后计算n=pxq,再由p和q算出另一个数z=(p-1)×(q-1),然后再选取一个与z互素的奇数e,e为公开指数;根据e值找出另一个值d,并能满足e×d=1 mod (z)条件。由此而得到的两组数(n,e) 和 (n,d)分别作为公钥 和私钥。 素数p、q以及z由密钥管理中心负责保密。在密钥对产生后将其销毁存入离线的安全库以备以后密钥恢复使用 。加密和解密过程都是模指数运算。使用公钥对明文加密得到密文C = M e mod( n) ;使用私钥解密密文得到明文 M= C d mod( n)。
例:
令p=3,q=11,得出n=p×q=3×11=33;z=(p-1)(q-1)=2×10=20;取e=3,(取一个跟20互素的数,3与20互质)则 e×d≡1 mod z,即3×d≡1 mod 20。
通过试算我们找到,当d=7时,e×d≡1 mod z
公钥为:(e,n)=(3,33),私钥为:(d,n)=(7,33) 明文为 M=5,密文C=5^3 mod 33 = 26(mod 33为除以33之后的余数) 解密过程 M= 26^7 mod 33 = 5
RSA算法的安全性:基于数论中的大整数分解困难问题,即计算两个大的质数的乘积很容易 ,而给定大整数寻找其因子则非常困难。
比如:4399 = 53 X 83 因此,大数n的位数长度非常关键,一般公司级 应用需要1024比特的n,重要的场合应该用2048 比特的n。
3.散列函数与数字签名
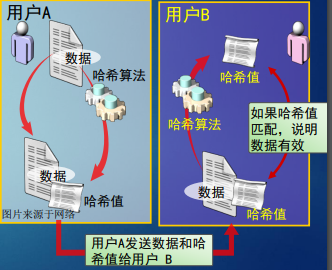
哈希函数
也称为Hash函数、杂凑函数、散列函数 ,是密码学中另一个非常重要的工具。
经典的哈希函数: MD5、SHA-1、SHA-3、SM3 ,可以将任意长度的一块数据转换为一个定长的哈希值,可以敏感地检测到数据是否被篡改,结合其他的算法可以用来保护数据完整性,只要输入改一比特,输出就会有巨大不同。
哈希函数的性质:
单向性:给定x容易计算H(x) ,反之则非常困难。
抗碰撞性:对于任意给定的分块x,找到满足 y≠x且H(x)=H(y)的y 在计算上是不可行的,通常认为哈希值和消息是一一 对应的。
哈希函数还可以用来保护用户口令——我们使用很多的登录系统 ,为了不在服务器上明文存放,不在网络上明文传输,一般都将口令做哈希运算 ,用户端哈希值发到服务器验证 ,只能做到一定程度的保护,还是有方法破解(彩虹表:把常见的字母组合、英文单词来进行哈希运算得到一个巨大的明文哈希值的对应表,当攻击者截获到用户的口令哈希值后只要经过查表运算就有可能恢复出来用户口令的明文)
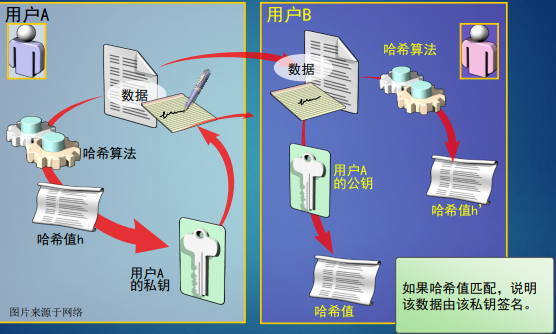
数字签名
是目前电子商务、电子政务中应用最普遍、技术最成熟的、可操作性最强的一种电子签名方法。它采用了规范化的程序和科学化的方法,用于鉴定签名人的身份以及对一项电子数据内容的认可。它还可以用来验证文件在传输过程中有无内容变动,确保传输数据的完整性、真实性和不可抵赖性。
常见的数字签名算法: RSA Data Security公司的PKCS(Public Key Cryptography Standards)、DSA(Digital Signature Algorithm)、X.509、PGP(Pretty Good Privacy) 、DSS等
密码的相对安全 :数学家香农创立的信息论中用严格的数学方法证明了一个结论:除了一次一密以外,一切密码算法,在理论上都是可以破解的。 没有绝对安全,只有相对安全 。
1.关于密码学学术流派说法错误的是
A. 编码密码学是由密码分析学发展而来
B. 密码学是在编码与破译的斗争实践中逐步发展起来的
C. 破译密码学也叫做密码分析学
D. 可以分为编码密码学和破译密码学
A. 对称密码体制也称做双钥密码体制
B. 加密、解密使用相同密钥的是对称密码体制
C. 非对称密码体制的加密密钥和解密密钥成对出现,从一个难于推算出另一个
3.关于密码学中的柯克霍夫原则,说法正确的是
A. 大多数民用加密系统都使用公开的算法
B. 大多数用于政府或军事机密的加密算法通常是公开的
C. 一个密码系统需要保密的越多,可能的弱点就越少
D. 密码算法应该和密钥一同保密
4.关于DES算法说法错误的是
A. 64比特的密钥中实际有效密钥长度为56比特
B. 64比特的密钥中含有8个比特的奇偶校验位
C. 是一个分组密码算法
D. 加密算法和解密算法是相同的
5.关于RSA算法说法错误的是
A. 基于大整数分解困难问题
B. 用于生成密钥的两个质数作为参数公开
C. RSA属于非对称密码体制


