树的整理

在csdn上很早发的

先列一个小母鹿吧

• 二叉树
• 基环树
• 虚树
• 仙人掌
• 圆方树
• 菊花图
• 带花树
• prufer序列

首先是推荐博客

• 树形dp+树形结构总结
• 树的细节整理 + 子链接

然后就是竖旗子 ： 每天整理两个吧

今天是二叉树，基环树

Day 1

树的概念

参考博客
在图论中，树被视作为一种特殊的图G=(V, E)，其中|V| = |E|+1。其存在如下特性：

1. 树G上任意两点必定能够通过途经若干边后到达
2. 任意两点间的路径必然唯一，即不存在环
3. 将树G上任意一条边删去，该图即成为非连通图
4. 在G中任意不相连两点间插入一条边，该新图G’ =(V, E’)正好含有一个环

二叉树

参考博客1
参考博客2

定义

二叉树是结点的一个有限集合，该集合或者为空，或者是由一个根结点加上两棵分别称为左子树和右子树的、互不相交的二叉树组成。

性质

• 第\(i(i \ge 1)\)层最多有\(2^{i - 1}\)个结点。
• 深度为\(k(k \ge 0)\)的二叉树最少有k个结点，最多有\(2^{k} - 1\)个结点。
• 对于任一棵非空二叉树，若其叶结点数为\(n_0\)，度为2的非叶结点数为\(n_2\)，则\(n_0 = n_2 + 1\)
• 具有n个结点的完全二叉树的深度至少为\(\lceil log_2 (n + 1) \rceil\)。
• 将一棵n个结点的完全二叉树自上而下，自左而右编号，有以下关系：

1. 若 \(ｉ= 1\)，则结点i为根，无父结点；若\(i > 1\)，则结点 i 的父结点为结点为\((i >> 1)\)
2. 若 \(2*i \le n\)，则结点 ｉ 左子结点\((i << 1)\)，右子节点\((i << 1 | 1)\)
3. 若结点编号ｉ为偶数，且\(i \ != n\)，它处于左兄弟位置，则它的右兄弟为结点\(i+1\)（反之亦然）
4. 结点ｉ所在的层为 \(\lfloor log_2i \rfloor + 1\)
5. 给定n个结点，能够成H(n)种不同的二叉树

*注：H(n)为卡特兰数。 \(H(n) = \frac{\tbinom{2n}{n}}{n + 1} = \frac{h(n-1)*(4*n-2)}{(n+1)} = \tbinom{2n}{n} - \tbinom{2n}{n-1}\)

特殊二叉树

（1）满二叉树
深度k的满二叉树是有2^k－1个结点的二叉树，在满二叉树中，每一层结点都达到了最大个数，除最底层结点的度为0外，其他各层结点的度都为2。

（2）完全二叉树
如果一棵具有n个结点的深度为k的二叉树，它的每一个结点都与高度为k的满二叉树中编号为1 ~ n－1的结点一一对应，则称这棵二叉树为完全二叉树。

（3）二叉查找树

定义：二叉查找树(Binary Search Tree)，又被称为二叉搜索树。设x为二叉查找树中的一个结点，x节点包含关键字key，节点x的key值记为key[x]。如果y是x的左子树中的一个结点，则key[y] <= key[x]；如果y是x的右子树的一个结点，则key[y] >= key[x]。

在二叉查找树中：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
2. 任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
3. 任意节点的左、右子树也分别为二叉查找树。
4. 没有键值相等的节点（no duplicate nodes）

遍历

前序遍历：中左右
中序遍历：左中右
后序遍历：左右中

相关术语

结点的度：结点拥有的子树的数目。
叶子：度为零的结点。
分支结点：度不为零的结点。
树的度：树中结点的最大的度。
层次：根结点的层次为1，其余结点的层次等于该结点的双亲结点的层次加1。
树的高度：树中结点的最大层次。
无序树：如果树中结点的各子树之间的次序是不重要的，可以交换位置。
有序树：如果树中结点的各子树之间的次序是重要的, 不可以交换位置。
森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

基环树

经典处理方式：

• 删掉环上的一条边变成树，然后再加回去分类讨论
• DP：先扣环，接着假设连在一起的两个点为u和v（u和v常存在限制关系，如不能同时选择），然后讨论选择u不选择v，选择v不选择u两种情况。
• 二元扣环参考

void get_loop(int u) {
    vis[u] = ++vs;
    for (int i = head[u]; ~i; i = edge[i].nxt) {
        int v = edge[i].to;
        if(v == fa[u]) continue;
        if(vis[v]) {
            if(vis[v] < vis[u]) continue;
            loop[++cnt] = v;
            for ( ;v != u; v = fa[v]) {
                loop[++cnt] = fa[v];
            }
        }
        else fa[v] = u, get_loop(v);
    }
}

• emm一元扣环的话。。直接找fa就好辣
  五道例题

Day 2

虚树

参考博客
有m次询问，每次询问给出k个点，当 \(2* ∑k\) 较小（比如1e6），且每次询问只能做到\(O(k)\)时食用

构造方式

（注意这里所有的lca都是p和x的lca）

首先我们要先对整棵树dfs一遍，求出他们的dfs序，然后对每个节点以dfs序为关键字从小到大排序
同时维护一个栈，表示从根到栈顶元素这条链上的点
假设当前要加入的节点为p，栈顶元素为x = s[top]，lca为他们的最近公共祖先
因为我们是按照dfs序遍历，因此lca不可能是p
那么现在会有两种情况

• lca是x，直接将p入栈。
• x,p分别位于lca的两棵子树中，此时x这棵子树已经遍历完毕，（如果没有，即x的子树中还有一个未加入的点y，但是dfn[y]<dfn[p]，即应先访问y）， 我们需要对其进行构建：

设栈顶元素为x，第二个元素为y

• 若dfn[y]>dfn[lca]，可以连边y−>x，将x出栈；
• 若dfn[y]=dfn[lca]，即y=lca，连边lca−>x，此时子树构建完毕(break)；
• 若dfn[y]<dfn[lca]，即lca在y,x之间，连边lca−>x，x出栈，再将lca入栈。此时子树构建完毕(break)。

仙人掌

仙人掌图（cactus）是一种无向连通图，它的每条边最多只能出现在一个简单回路（simple cycle）里面。从直观上说，可以把仙人掌图理解为允许存在回路的树。但是仙人掌图和树之间有个本质的不同，仙人掌图可以拥有多个支撑子图（spanning subgraph），而树的支撑子图只有一个（它自身）。
来自luogu

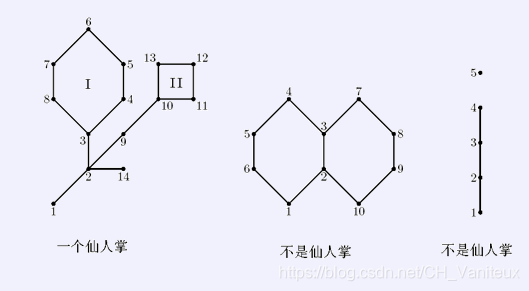
图源BZOJ1023 OrzOrz

结论：仙人掌的支撑子图数\(Ans=∏i​(siz[i]+1)\)

DFS树

貌似。。就是单纯的DFS。。。但因为因为每条边只会出现在一个环中，所以每一条返祖边覆盖了树中的一条链，这条链和这条边就构成环。
仙人掌最大独立集
仙人掌直径
bzoj
luogu

模板

void dfs(int x, int ff){
	fa[x] = ff; 
	dfn[x] = low[x] = ++dfncnt;
	dep[x] = dep[ff] + 1;
	for(int i = head[x], vv; ~i; i = edge[i].next){
		vv = edge[i].v;
		if(vv == ff) continue;
		if(!dfn[vv]){
			dfs(vv, x);
			low[x] = min(low[vv], low[x]);
		}
		else low[x] = min(low[x], dfn[vv]);
		
		if(low[vv] > dfn[x]){
			//维护答案 及 圆圆边（树边）转移
		} 
	}
	for(int i = head[x], vv; ~i; i = edge[i].next){
		vv = edge[i].v;
		if(fa[vv] != x && dfn[x] < dfn[vv]) 
		    dp(x, vv);
	}
}

Day 3

圆方树

参考yyb的博客

对于一个仙人掌， 保留它原来所有的点，称为圆点。
对于它的每一个环，新建一个方点，连向环里所有的点，并删除环上原来的边
长成这样子

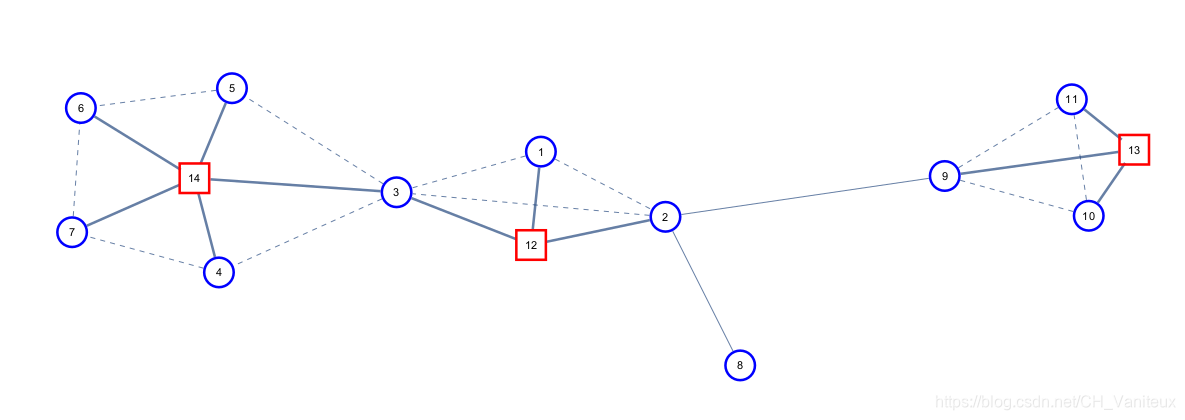
图源yyb的博客

例题：仙人掌最短路

性质：

1. 方点不会直接和方点相连
2. 无论取哪个点为根，圆方树的形态是一样的
3. 以r为根的仙人掌上p的子仙人掌就是圆方树中以r为根时，p子树中的所有圆点

定义：子仙人掌
以r为根的仙人掌上的点p的子仙人掌是去除掉p到r的所有简单路径后，p所在的联通块

广义圆方树

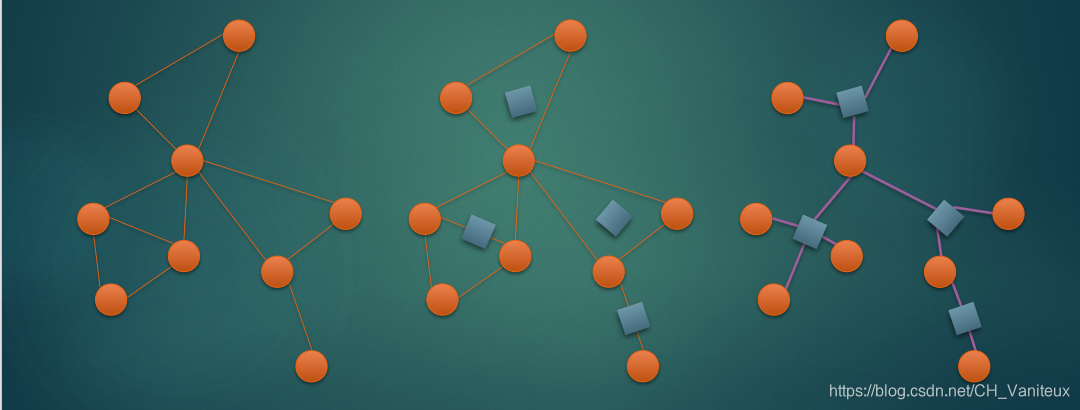
图源租酥雨的博客

例题：带修无向图路径最小值
luogu

菊花图

就是一个所有点都和根相连的图啦
注意yy出一个做法后想想菊花图能不能卡掉（比如上面tourists那道）

带花树

stO yyb Orz
对于一般图的匹配问题 匈牙利遇到奇环就挂掉了
于是有了带花树
简单来讲 带花树算法=匈牙利算法+处理奇环
核心部分

int findf(int x){//并查集
    return x == fa[x] ? x : fa[x] = findf(fa[x]);
}

int lca(int x, int y){//暴跳lca
    ++tim; x = findf(x); y = findf(y);
    while(dfn[x] != tim){
        dfn[x] = tim;
        x = findf(pre[match[x]]);
        if(y) swap(x, y);
    }
    return x;
}

queue<int> que;

void Blossom(int x, int y, int LCA){//开花花
    while(findf(x) != LCA){
        pre[x] = y, y = match[x];
        if(vis[y] == 2){
            vis[y] = 1; que.push(y);
        }
        if(findf(x) == x) fa[x] = LCA;
        if(findf(y) == y) fa[y] = LCA;
        x = pre[y];
    }
}

bool HA(int x){//拟匈牙利匹配
    for(int i = 1; i <= n; ++i)fa[i] = i;
    memset(vis, 0, sizeof(vis));
    memset(pre, 0, sizeof(pre));
    while(!que.empty()) que.pop();
    que.push(x); vis[x] = 1;

    while(!que.empty()){
        int fro = que.front(); que.pop();
        for(int i = head[fro]; ~i; i = edge[i].next){
            int vv = edge[i].v;
            if(findf(fro) == findf(vv) || vis[vv] == 2)
                continue;
            if(!vis[vv]){
                vis[vv] = 2; pre[vv] = fro;
                if(!match[vv]){
                    for(int j = vv, lst; j; j = lst){
                        lst = match[pre[j]], match[j] = pre[j], match[pre[j]] = j;
                    }
                    return 1;
                }
                else{
                    vis[match[vv]] = 1, que.push(match[vv]);
                }
            }
            else {
                int LCA = lca(fro, vv);
                Blossom(fro, vv, LCA);
                Blossom(vv, fro, LCA);
            }
        }
    }
    return 0;
}

prufer序列

[HNOI2008]明明的烦恼
给出标号为1到N的点,以及某些点最终的度数,允许在任意两点间连线,可产生多少棵度数满足要求的树?（\(1 \le n \le 1000\)）
安利博客