渗透模型 Percolation Models（一个物理模型的广泛应用）

转自：http://mooc.guokr.com/note/15357/

http://mooc.guokr.com/user/0298406005/note/

模型思想：

有水流下来，是否会渗入地面？

 

像棋盘一样的格子，可以空白也可以被填满

你只可以从一个被填充的方格跳到相邻的另一个被填充的方格

 

像这样就不会渗透，因为所有黑色的路都被堵死了，水不会从上面流到底部

 

 

假设每个格子被填充的概率是相等的，设为P

P=1/2，有一半的格子被填满

P=1/3，有1/3的格子被填满，剩下2/3,没有

——问题：这个模型渗透吗？

 

这个模型曲线是这样的

 

只要P低于59.2%，就不会渗透

超过这个点之后，系统就会引爆

是什么创造出了这个点？

被填满的格子如果从20%增加到21%，或者从21%增加到22%，都不会有什么变化，但是如果从58%-59%，就会有一个突然的变化

 

这个模型可以有很多应用领域

 

1、森林火灾模型，把树的密度设置在57%，开始点火，只差一点儿就成功了

 

然后把它调到61%，让它高于59%的阈值，于是一下就成功了

 

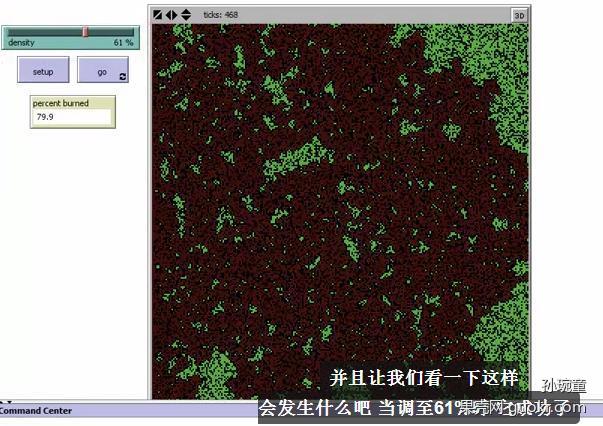
假设我们有一片森林，我们希望它的产量越多越好，但又有发生火灾的可能性

那么收成曲线会是怎样的？

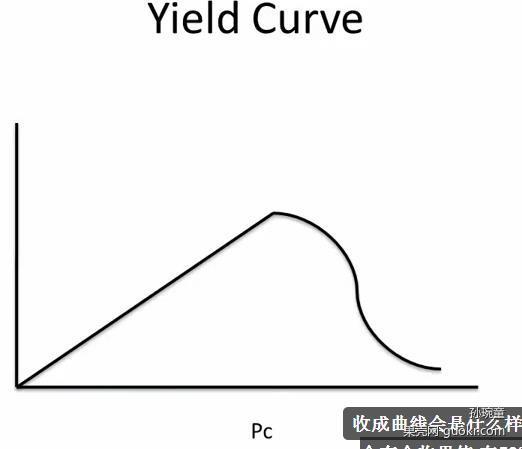
在59%以前，我们会得到一个漂亮的线性曲线，森林覆盖越多，得到的木材也越多

但一旦超过临界值，我们的收成就会急剧跌落

 

2、银行渗透模型

假设有5个银行，中间的银行1倒闭了，它有很多不良贷款，假设银行1向银行2,3,4,5借过钱，当银行1倒闭时，它不能偿还这些钱，其他银行可能会跟着倒闭，这个失败就会蔓延开来

问题：如果银行倒闭，会蔓延多远？也存在一个临界点吗？

 

 

3、再比如国家失败的模型

如果一个国家衰败了，其他的国家会被渗透到吗？

 

 

4、信息渗透

假设有一个人际网络，如果我听到了一些传闻，我会去告诉我的朋友们，那么有多大的可能性事情会传播开来？我们可以用同样的模型

你可能会以为信息的价值越大，被传播到的人数就越多，这是一个线性模型，但如果你真的建立了一个人际网络，很有可能会出现一个引爆点，即使不那么重要的信息，一旦超过阈值，就会扩散至整个人群

 

引爆点在我们的生活中很常见

例如一些数学问题、工程问题等，人们往往致力于它们很多年，但是一直没有突破，但突然之间有一大部分人几乎在同一时间解决了这个问题

为什么我们经常看到某个领域科学活动的突然爆发？也可以用渗透模型解释

——随着知识和信息的积累，我们会填充更多的格子