详解OpenGL中的各种变换（投影变换，模型变换，视图变换）（一）——模型变换和视图变换

本文一些用于均参考《OpenGL编程指南（第8版）》，有兴趣的同学可以结合一起看。这篇算是整合补充。

　　OpenGL采用的是相机模型，就是把视图变换操作类比为使用照相机拍摄照片的过程，具体步骤如下（这里和红宝书有一些改变）：

1. 将准备拍摄的对象移动到场景中指定位置。（模型变换，Model Transform）
2. 将相机移动到准备拍摄的位置，将它对准某个方向。（视图变换，View Transform）
3. 设置相机的焦距，或者调整缩放比例。（投影变换，Projection Transform）
4. 拍摄照片并变换到需要的图片大小。（这个是视口变换，我们这里不做讨论）

　　在这四个步骤中，前三个都是可以用变换矩阵实现的。看完本文之后基本就可以用自己写的矩阵来代替OpenGL里面的各种变换操作了。至于为什么要按照上述的顺序可以参考下面代码，有兴趣的读者可以调换一下位置试一试，其中投影变换矩阵一定要放在最左边。

1 2 3 4

/*Project：投影变换矩阵     View：视图变换矩阵     Model：模型变换矩阵*/ ModelViewProject = Project * View * Model;

 

---

　　下面需要知道一些矩阵和齐次坐标的相关知识，网上有很多资料，如果又不知道的可以提前了解下。

　　这里有必要深入讲解一下齐次坐标的意义。假设一3维向量x，我们对这个向量进行线性变换Tx，但无论T为任意3*3矩阵，都无法完成向量的平移操作（比如x=(0,0,0)，Tx无论如何也不可能变换到(1,0,0)）。这里我们就需要用到齐次坐标，使用齐次坐标的目的也就是通过增加额外的数值来完成向量的平移操作。熟悉OpenGL的已经知道了，将三维数据植入思维坐标空间当中就行了。就是将x=(0,0,0)转变成x=(0,0,0,1)。T也转变成4*4矩阵。

　　我们再讨论一下齐次坐标的一个性质， 齐次坐标所表达的其实是方向而不是位置。比如x₁=(1,2,3,1)和x₂=(2,4,6,2)其实在3维坐标系中表示的是同一个位置。此外，最后一个分量w越大，那么齐次坐标将处于更远的位置。当OpenGL准备显示集合体的时候，它会使用左后一个分量除以前三个分量，从而将其次坐标重新变换到3维坐标系中，因此w越大的物体也会显示的越小。w为0.0的时候，由于坐标位于无限近的位置，以至于显示可能会呈现出无限大。这个概念非常重要，因为下面投影矩阵就是利用这个概念！

　　我们接下来说明三个变换中具体包含哪些矩阵。对于一个顶点来说，我们对其先进行模型变换，在进行视图变换和投影变换。我们将这些变换细分一下就可以得到如下代码：

1 2 3 4 5

/*S：缩放 R：旋转 T：平移*/ ModelViewProject = Project 　　　　　　　　　　* ViewR * ViewT 　　　　　　　　　　* ModelS * ModelR * ModelT gl_position = ModelViewProject * Vertex;

　　

---

 　　下面我就按照顺序逐一介绍一下各个矩阵，先介绍一下模型变换矩阵，这部分我就不细说了，了解的人应该不少。

　　（1）ModelT 平移矩阵

　　这个矩阵算是最简单的矩阵，这里举个例子。假设我们要将v=(x,y,z)沿x轴正方向平移2.5，具体计算如下：

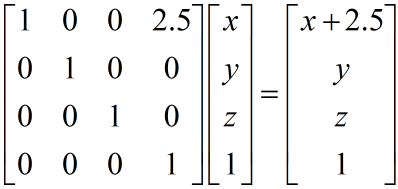
图1

　　（2）ModelR 旋转矩阵

　　这个矩阵就比较多样了，我以前的博客关于这个矩阵有不少分析，这里也不多说了。下面列出三个欧拉角对应的旋转矩阵（也是最常用的）：

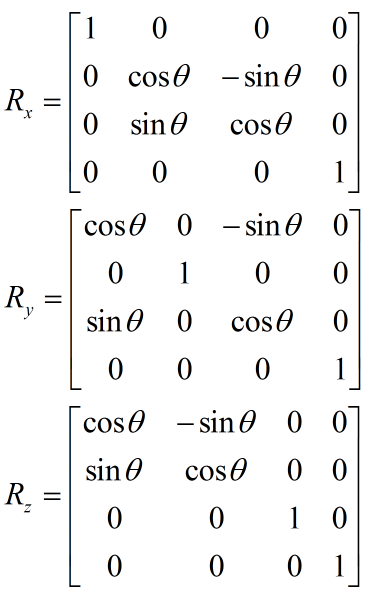
图2

　　（3）ModelS 缩放矩阵

　　这个矩阵也比较简单，只要把缩放因子factor放在矩阵的对角线上就行了。具体表达如下：

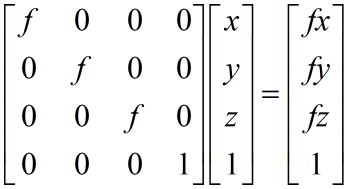
图3

　　这三个矩阵就组成了模型变换矩阵，根据具体需求可以随意组合平移旋转缩放矩阵，并不一定非要按照上面代码中的顺序。

 

---

　　下面介绍视图矩阵，我们可以把这一步假想为设置相机或者人眼（View）的位置。设置相机一般只需要两步，首先把相机移动到固定的位置，然后把当前坐标系转化成相机坐标系。这里不像模型变换，可以多次旋转平移，这里只需要1个平移操作和1个旋转操作一般就可以了，而且还不需要缩放。

　　（1）ViewT 平移矩阵

　　这个矩阵和ModelT正好是相反的。我们可以这样理解，如果要在世界坐标系下的(x,y,z)位置设置相机，那么我们把相机再移回世界坐标系原点的位移就是(-x,-y,-z)。所以我们当以相机为坐标原点的时候，所有在原来坐标系下的物体都要加上这个负的平移分量。那么这个平移矩阵如下：

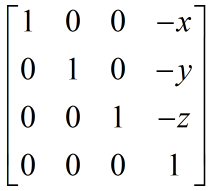
图4

　　（2）ViewR 旋转矩阵

　　我们将原来的坐标系转变成相机坐标系，不仅需要平移到相机位置，还要旋转到相机的朝向。如图5所示，我们要将蓝色的坐标系通过旋转变换成红色的相机坐标系。由于坐标系的三个基向量都是单位化的，所以最简单的办法就是点乘。做法是点乘相机坐标系的三个基向量，具体看图6的公式。

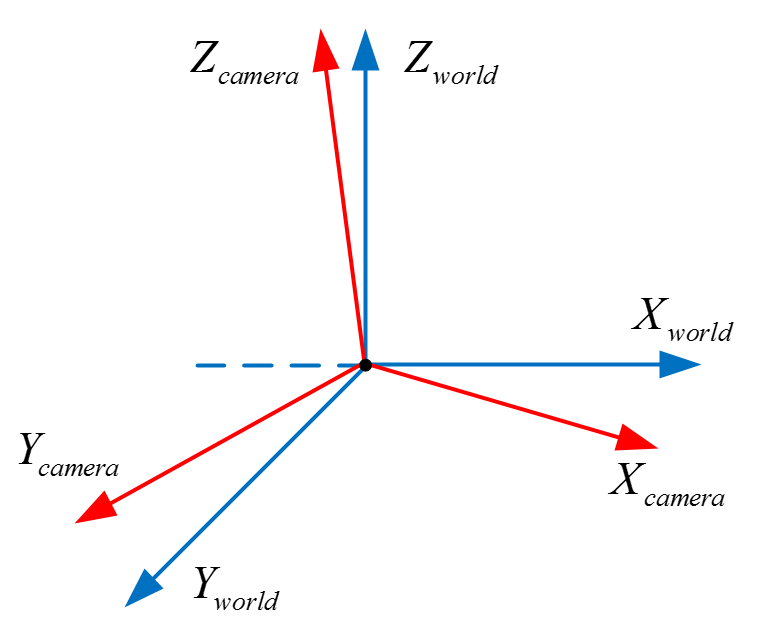
图5

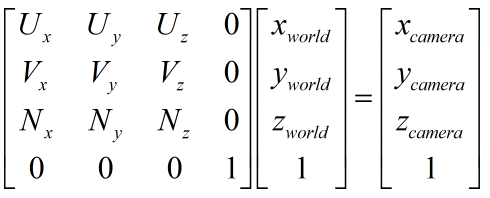
图6

 

　　其中V指向相机坐标系的y轴，U指向相机坐标系的x轴，N指向相机坐标系的z轴。

　　这两个矩阵就组成了视图变换矩阵，将View乘以Model得到的矩阵，在OpenGL固定管线中称为模型视图矩阵，可以通过glMatrixMode(GL_MODELVIEW)进行设置。