计算概论（一）计算起源、图灵机、计算原理

计算概论（一）计算起源、图灵机、计算原理

apigfly 2020-08-08 15:34:45  148  收藏

分类专栏： 计算概论 文章标签： 计算概论 图灵机 半加器 全加器 java

版权

本篇是对北大信息技术学院李戈老师计算概论与程序设计基础课程的笔记和总结，源课程地址

中国大学MOOC的课程是真的不错，一句好的大学 没有围墙让人有些心生感动哇，哈哈哈。

PS：本人真滴不是托哈

计算起源

三次数学危机到哥德尔不完备性定理，产生了可计算与不可计算的边界问题。而对于边界问题探讨，引发了图灵机的问世。

第一次数学危机（无理数发现）

故事开始于公元前500年

毕达哥拉斯学派

信仰：

• 数是万物的本源，事物的性质是由某种数量关系决定的，万物按照一定的数量比例而构成和谐的秩序。
• 一切数均可表示为整数或整数之比

后来，毕达哥拉斯还证明了勾股定理，但是同时发现『某些直角三角形的三边比不能用整数来表达』，由于各种原因毕达哥拉斯没有公布，后来希帕索斯也发现了并且公布了出来。

希帕索斯悖论

希帕索斯考虑了一个问题 ：边长为1的正方形其对角线长度是多少呢？

• 当时还没有无理数的概念，其对角线“√2”自然无法用两个整数的比值来表示
• 毕达哥拉斯的其他门徒知道后，为了维护门派的正统性，把希帕索斯杀害，并抛入大海之中。

数学危机由此开始。

危机缓解

二百年后，欧多克索斯借助几何学的方法，建立起一套完整的比理论，避开了无理数的问题

危机解决

19世纪下半叶，实数理论建立后，无理数本质被彻底搞清。
无理数在数学中合法地位的确立，才真正彻底、圆满地解决了第一次数学危机。

第二次数学危机（微积分）

十七世纪，牛顿和莱布尼兹各自独立发现了微积分，但两人的理论都是建立在无穷小的分析之上。

贝克莱悖论

无穷小量在牛顿的理论中『一会儿是零，一会儿又不是零』

从微积分的推导中我们可以看到，△x在作为分母时不为零，但是在最后的公式中又等于零，这种矛盾的结果是灾难性的，很长一段时间内数学家都找不到解决办法。

危机解决

微积分发明100多年后，法国数学家柯西用极限定义了无穷小量，才彻底解决了这个问题。

第三次数学危机（集合论）

数学家总有一个梦想，试图建立一些基本的公理，然后利用严格的数理逻辑，推导和证明数学的所有定理。
康托尔发明集合论后，法国科学家庞加莱认为：我们可以借助集合论，建造起整座数学大厦。

罗素悖论

S 由一切不是自身元素的集合所组成。那么 S 是否属于 S 呢？

罗素悖论通俗描述为：在某个城市中，有一位名誉满城的理发师说：“我将为本城所有不给自己刮脸的人刮脸，我也只给这些人刮脸。”那么请问理发师自己的脸该由谁来刮？

危机解决

数学家辛辛苦苦建立的数学大厦，最后发现基础居然存在缺陷，数学家们纷纷提出自己的解决方案；直到1908年，第一个公理化集合论体系的建立，才弥补了集合论的缺陷。

虽然三次数学危机都已经得到了解决，但是对数学史的影响是非常深刻的，数学家试图建立严格的数学系统，但是无论多么小心，都会存在缺陷

哥德尔不完备定理

任何一个数学系统，只要它是从有限的公理和基本概念推导出来的，并且从中能推导出自然数系统，就可以在其中找到一个命题，对于它我们既没有办法证明，又没有办法推翻

第一定理

任意一个包含一阶谓词逻辑与初等数论的形式系统，都存在一个命题，它在这个系统中既不能被证明为真，也不能被证明为否。

第二定理

如果系统S含有初等数论，当S无矛盾时，它的无矛盾性不可能在S内证明。

哥德尔不完备性定理宣告了把数学彻底形式化的愿望是不可能实现的

可计算边界问题

虽然哥德尔不完备性定理宣告了把数学彻底形式化的愿望是不可能实现的。但我们还是希望明确哪些问题可以被证明（计算），哪些不可以。这就是可计算的边界问题

数学家给出了研究思路：为计算建立一个数学模型，称为计算模型，然后证明，凡是这个计算模型能够完成的任务，就是可计算的任务。

而图灵针对这个问题提出了一个模型，这个模型就是图灵机

图灵和图灵机

说道图灵机，那就得先说计算机历史上值得铭记的人Alan Turing

图灵

看看人家的简历：

• 1912年6月，生于伦敦
• 中学期间，获国王爱德华六世数学金盾奖章
• 1935年，被选为剑桥大学国王学院院士
• 1936年5月，图灵提出图灵机，(发表于《伦敦数学会文集》)
• 1938年，美国普林斯顿大学获博士学位
• 1938-1945年二战期间，密码破译工作(曾任英美密码破译部门总顾问)
• 1946年，获不列颠帝国勋章
• 1950年，提出著名的“图灵测试”
• 1950年10月，发表论文“机器能思考吗”(开启了人工智能的研究)
• 1951年，被选为英国皇家学会会员(家族中第四位皇家学会会员)
• 1952年，图灵写出一个国际象棋程序
• 1954年，逝世

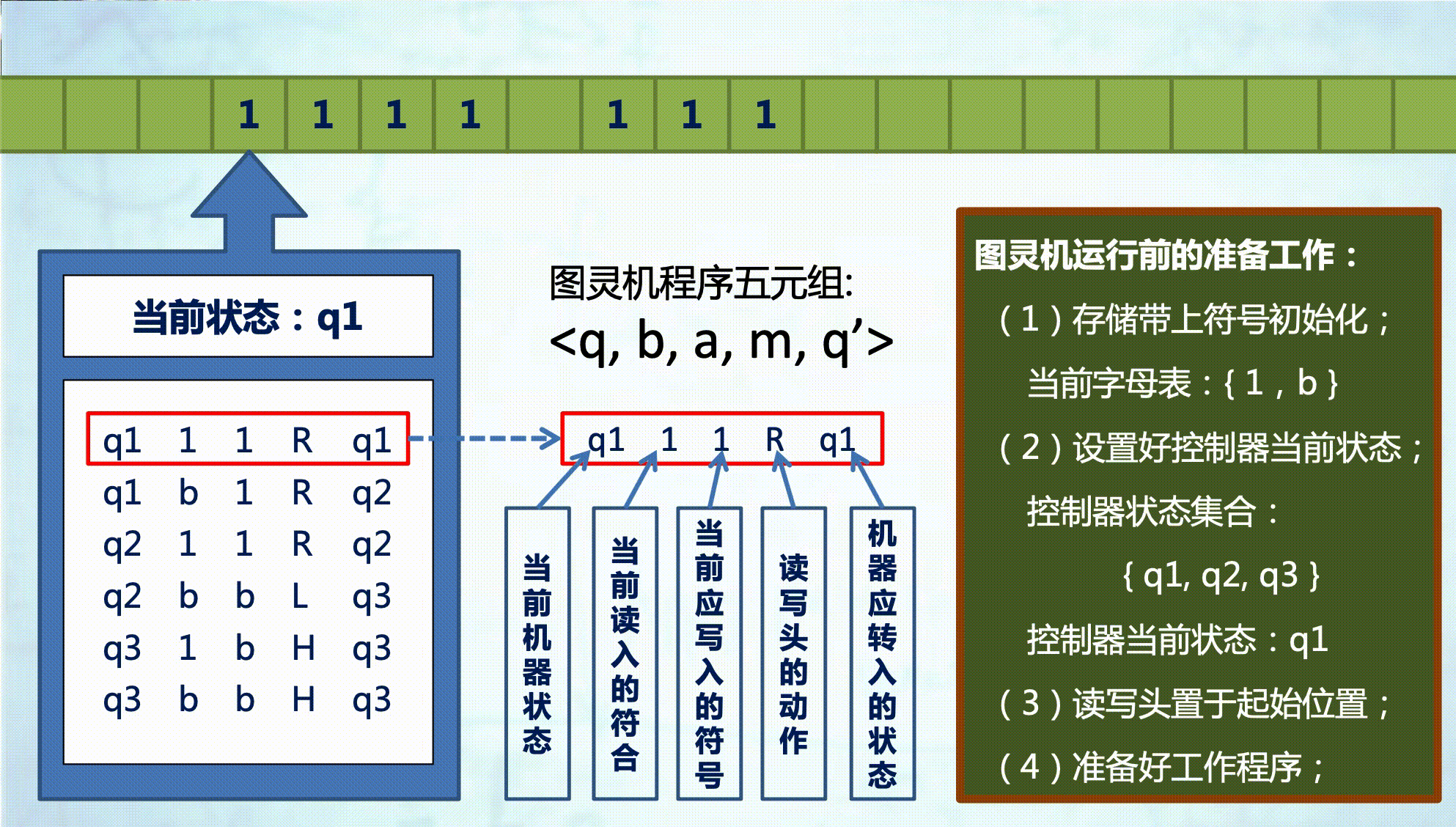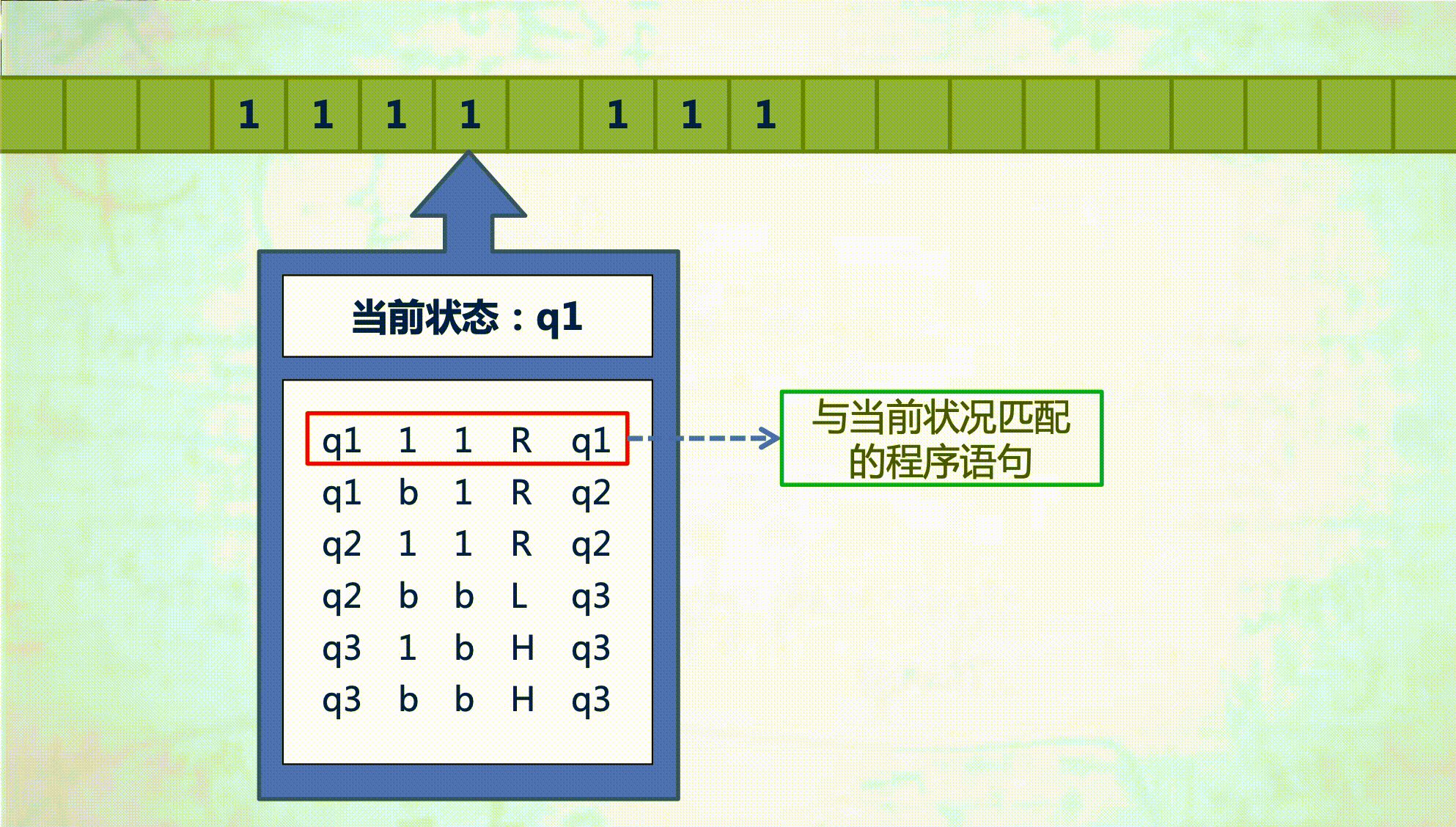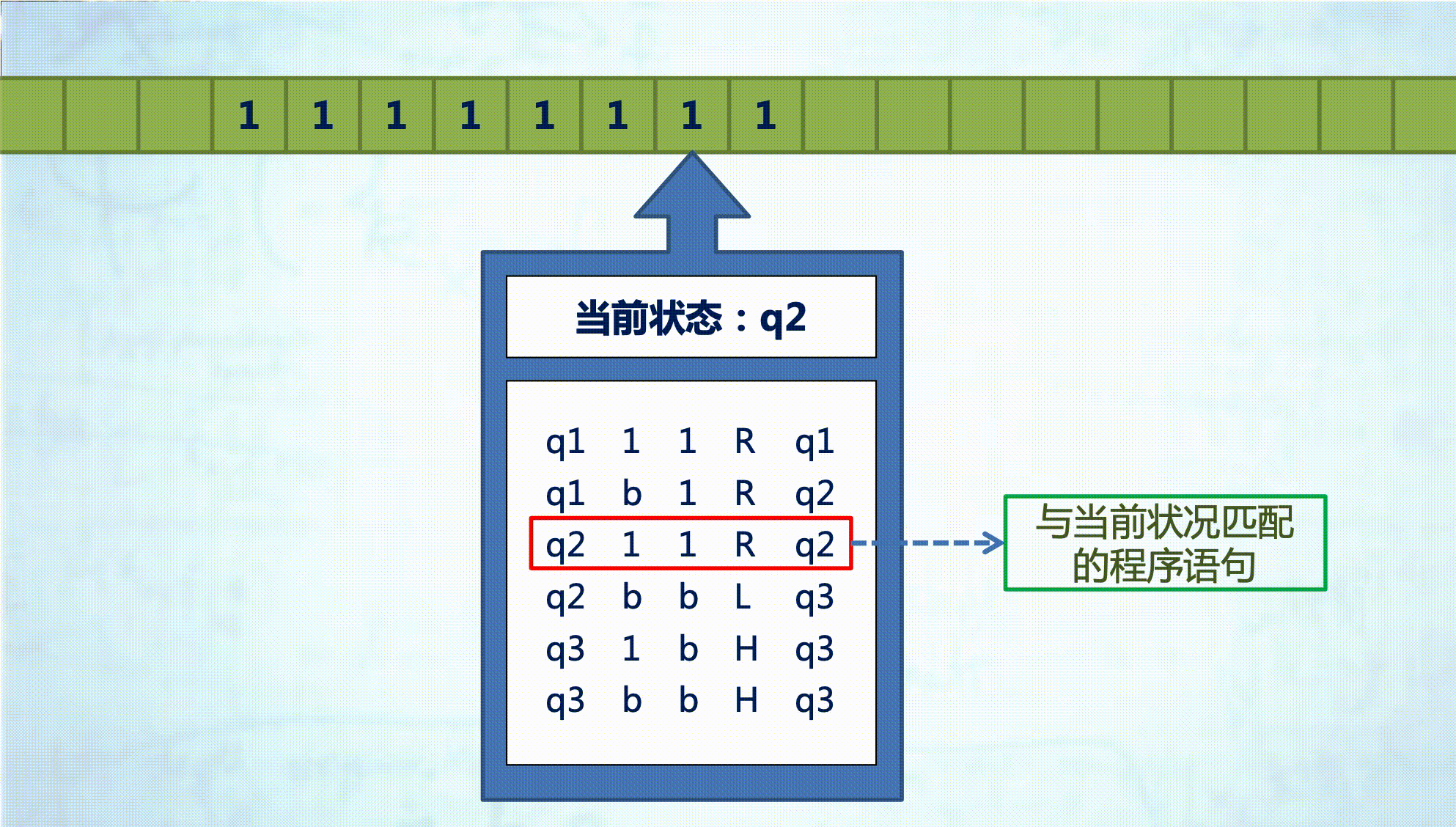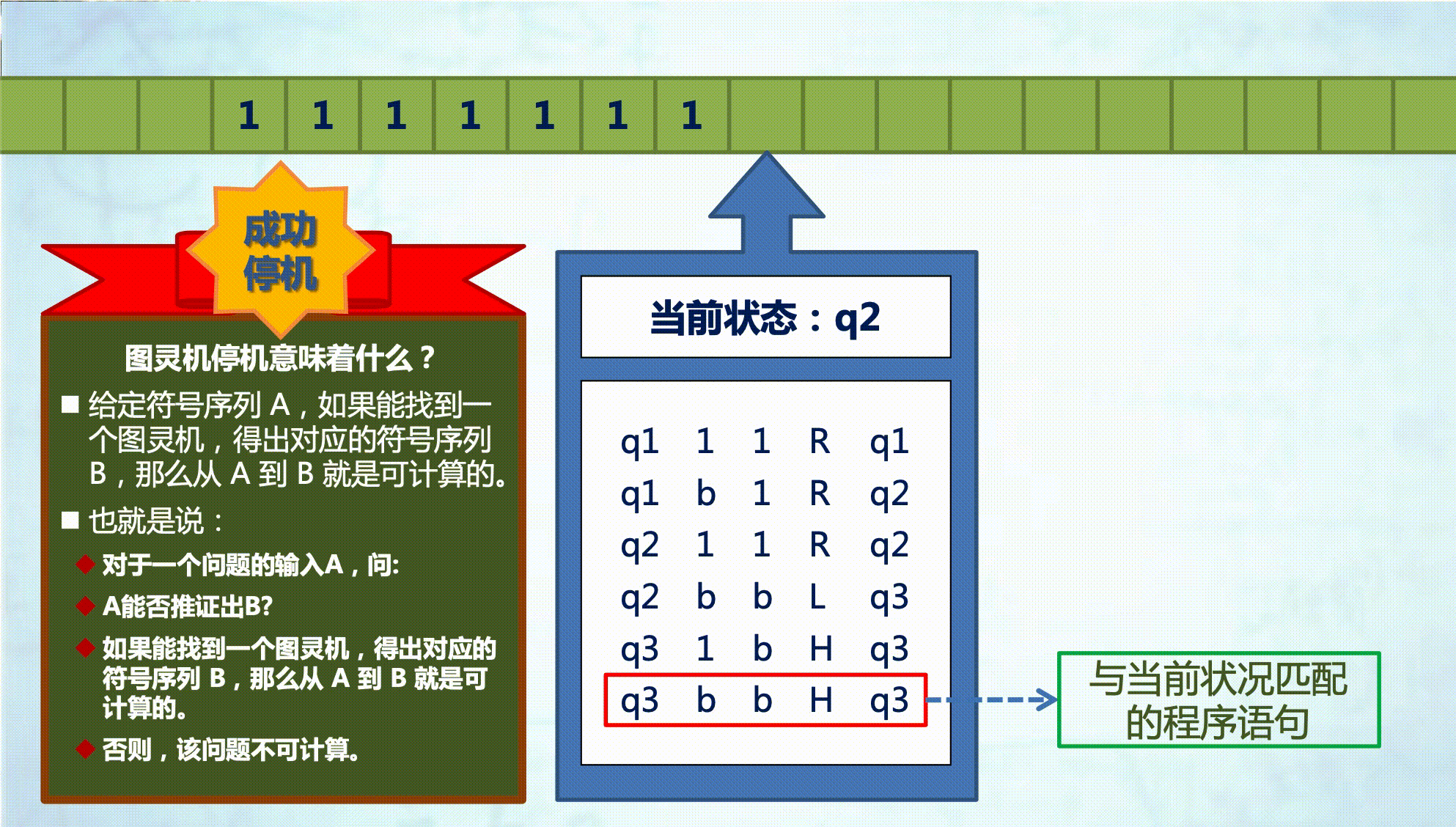
1936年，图灵在其著名的论文《论可计算数在判定问题中的应用》一文中提出了一种理想的计算机器的数学模型——图灵机 (Turing Machine )。

图灵机

图灵机的组成

这是一张有些模糊但是很清晰的图片：

一条存储带

• 双向无限延长
• 上有一个个小方格
• 每个小方格可存储一个数字/ 字母

一个控制器

• 可以存储当前自身的状态;
• 包含一个读写头，可以读、写、更改存储带上每一格的数字/字母
• 可以根据读到的字母/数字变换自身的状态
• 可以沿着存储带

图灵机的工作步骤

1. 准备:
   • 存储带上符号初始化;
   • 控制器设置好自身当前状态;
   • 读写头置于起始位置;
   • 准备好工作程序;
2. 反复执行以下工作直到停机:
   • 读写头读出存储带上当前方格中的字母/数字;
   • 根据 自身当前状态 和 所读到的 字符，找到相应的程序语句;
   • 根据 相应程序语句，做三个动作:
     • 在当前存储带方格上写入一个相 应的字母/数字;
     • 变更自身状态至新状态;
     • 读写头向左或向右移一步;

图灵机的理论意义

• 可计算性的判定：

  给定符号序列 A，如果能找到一 个图灵机，得出对应的符号序列 B，那么从 A 到 B 就是可计算的。

• 给出了一个可实现的通用计算模型;

• 引入了通过“读写符号” 和“状态改变”进行运算的思想;

• 证实了基于简单字母表完成复杂运算的能力;

• 引入了存储区、程序、控制器等概念的原型;

计算机为什么能计算？

我们都知道计算机中的数使用二进制来表示，那么计算机是怎么完成计算的呢？

我们先来铺垫一个知识点布尔代数

布尔代数

1854年G Boole发表《思维规律的研究——逻辑与概率的数学理论基础》，并综合其另一篇文章《逻辑的数学分析》，创立了一门全新的学科-布尔代数。为计算机的开关电路设计提供了重要的数学方法和理论基础。

逻辑运算方法

逻辑与

电路图：

函数表达式：F = A * B

真值表：

A	B	=F
0	0	=0
0	1	=0
1	0	=0
1	1	=1

逻辑或

电路图：

函数表达式：F = A + B

真值表：

A	B	=F
0	0	=0
0	1	=1
1	0	=1
1	1	=1

逻辑非

电路图：

真值表：

A	=F
0	=1
1	=0

同或

• 两数相同为“1”
• 两数相异为“0”

异或

• 两数相同为“0”
• 两数相异为“1”

计算方式

常规的计算方法

举例: A=0b1101, B=0b1001, 求 A+B。

按照常规计算方式，是这样的：

计算机的计算方式

先看下半加器

通过多个半加器的组合，我们就可以得到全加器

再次提问：计算机为什么能计算？

了解到这里我们就可以解答了：

• 首先，数字运算可以转换二进制数的运算;
• 二进制运算可以转换为基本的布尔运算;
• 基本的布尔运算都可以由电路完成;
• 计算机是由这些基本电路组成

所以计算机具有计算能力。

再专业一点的描述ALU

我们上面描述的布尔运算和计算方式两部分就是组成计算机ALU的两个核心单元：

• 逻辑单元：执行逻辑操作，比如：与、或、非等
• 算术单元：负责计算机中所有数字操作

既然这样，就用代码来模拟实现一个全加器吧！

加法器实现

先看下一个示意图：

代码示例：

public class ALU {
    /**
     * 半加器
     *
     * @param a 待加数
     * @param b 待加数
     * @return 半加后的本位和进位
     */
    public int[] halfAdder(int a, int b) {
        int carry;
        int sum;
        sum = XOR(a, b);
        carry = AND(a, b);
        return new int[]{sum, carry};
    }

    /**
     * 全加器
     *
     * @param a 待加数
     * @param b 待加数
     * @param c 待进位数
     * @return 全加后的本位和进位
     */
    public int[] fullAdder(int a, int b, int c) {
        int carry;
        int sum;
        int[] first = halfAdder(a, b);
        int[] second = halfAdder(first[0], c);
        sum = second[0];
        carry = OR(second[1], first[1]);
        return new int[]{sum, carry};
    }

    /**
     * 异或运算
     */
    public int XOR(int a, int b) {
        return a ^ b;
    }

    /**
     * 与运算
     */
    public int AND(int a, int b) {
        return a & b;
    }

    /**
     * 或运算
     */
    public int OR(int a, int b) {
        return a | b;
    }

    /**
     * 8 位加法器，一步一个脚印版本
     *
     * @param binaryA 二进制数组
     * @param binaryB 二进制数组
     * @return 二进制
     */
    public int[] FullAdder_8_Bit(int[] binaryA, int[] binaryB) {
        int[] out = new int[8];
        int[] first = halfAdder(binaryA[7], binaryB[7]);
        out[7] = first[0];
        int[] second = fullAdder(binaryA[6], binaryB[6], first[1]);
        out[6] = second[0];
        int[] three = fullAdder(binaryA[5], binaryB[5], second[1]);
        out[5] = three[0];
        int[] four = fullAdder(binaryA[4], binaryB[4], three[1]);
        out[4] = four[0];
        int[] five = fullAdder(binaryA[3], binaryB[3], four[1]);
        out[3] = five[0];
        int[] six = fullAdder(binaryA[2], binaryB[2], five[1]);
        out[2] = six[0];
        int[] seven = fullAdder(binaryA[1], binaryB[1], six[1]);
        out[1] = seven[0];
        out[0] = seven[1];
        System.out.println(Arrays.toString(out));
        return out;
    }

    /**
     * 优化版本，自定义加法器长度
     *
     * @param binaryA 待加数组
     * @param binaryB 待加数组
     * @param bitLen  运算长度
     * @return 计算后的数组长度
     */
    public int[] FullAdderBits(int[] binaryA, int[] binaryB, int bitLen) {
        int[] out = new int[bitLen];
        int[] tmpRes;
        int[] first = halfAdder(binaryA[7], binaryB[7]);
        out[bitLen - 1] = first[0];
        tmpRes = first;
        for (int i = bitLen - 1; i > 0; i--) {
            tmpRes = fullAdder(binaryA[i], binaryB[i], tmpRes[1]);
            out[i] = tmpRes[0];
        }
        out[0] = tmpRes[1];
        System.out.println(Arrays.toString(out));
        return out;
    }

    public static void main(String[] args) {
        ALU alu = new ALU();
        //                 {高位-----------低位}
        int[] a = new int[]{0, 1, 1, 1, 0, 0, 1, 0};//114
        int[] b = new int[]{0, 0, 1, 1, 0, 0, 1, 1};//51
        alu.FullAdder_8_Bit(a, b);
        alu.FullAdderBits(a, b, 8);
    }
}

我们看下测试输出：

[1, 0, 1, 0, 0, 1, 0, 1] //165
[1, 0, 1, 0, 0, 1, 0, 1] //165

• 1
• 2

有木有、有木有，代码中完全没有 +，—，*，/（请忽略for循环哈！），完全是通过逻辑运算实现。